С помощью графического метода может быть решена ЗЛП, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если n и m связаны соотношением n-m=2. Действительно, пусть поставлена ЗЛП:
найти минимальное значение линейной функции Z =C1x1+ С2x2 +...+ Сn xn при ограничениях
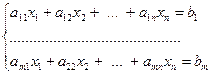xj 
0 , (j=1,2,…,n).
где все уравнения линейно независимы и выполняется соотношение n-m =2.
Используя метод Жордана - Гаусса, производим т исключений, в результате которых базисными неизвестными будут, например, т первых неизвестных x1,x2,..., x m, а свободными - два последних:.xm+1 и xn, т. е. система ограничений приняла вид
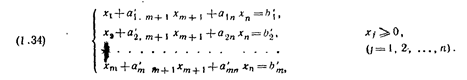
С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные неизвестные - неотрицательные: xj 0 (j=1,2,..., т),отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств. Таким образом, окончательно получаем следующую задачу: найти минимальное значение линейной функции Z = C'm+1xm+1 + C'nxnпри ограничениях
Преобразованная задача содержит два неизвестных; решая ее графическим методом, находим оптимальные значения xm+1 и хn, а затем, подставляя их в (1.34), находим оптимальные значения x1,x2,…xm.
Пример. Графическим методом найти оптимальный план ЗЛП Z=2х1-х2+x3-3x4+4х5®max при ограничениях 
xj 0 (j= 1,2,..., 5).
Решение. Используя метод Жордана — Гаусса, производим 3 полных исключения неизвестных х1, х2, х3.
| X1 | X2 | X3 | X4 | X5 | B |
| -1 -1 -2 | -18 -21 -43 | -4 | |||
| -1 | -2 -1 | -18 | -4 | ||
| -2 | -3 -4 | ||||
| -4 | -3 |
В результате приходим к системе:
(1)
откуда х1=6-х4+3х5, х2=70-7х4-10х5, х3=20+4х4-5х5. (2) Подставляя эти значения в линейную функцию и отбрасывая в системе (1) базисные переменные, получаем задачу, выраженную только через свободные неизвестные переменные х4 и х5: найти максимальное значение линейной функции Z = 6x4 +15x5-38 при ограничениях 
Построим многогранник решений и линейную функцию в системе координат x40 x5. Из рис. заключаем, что линейная функция принимает максимальное значение в угловой точкеВ, которая лежит на пересечении прямых 2 и 3. В результате решения системы
находим:x4 = 2,x5= 28/5. Максимальное значение функция Zmax =- 38+ +12+84-58.
Для отыскания оптимального плана исходной задачи, подставляем в (2) найденные значения x4 и х5. Окончательно получаем: х1 = 104/5, х2 =0, х3 =0, х 4 = 2, x5 = 28/5.
Контрольные вопросы
1. Графический метод решения задач линейного программирования с двумя переменными.
Рекомендованная литература: [ 2, 5, 8, 11, 12]
Тема 5. СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Розглянуті питання з теми:
5.1. Геометрическая интерпретация симплексного метода
Алгоритм симплекс-метода
5.3. Пример отыскания максимума линейной функции
5.4. Пример отыскания минимума линейной функции
5.5. Симплексные таблицы
5.6. Метод искусственного базиса
