Расстояние между двумя точками 
и 
находится по формуле
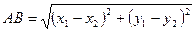. (6)
Например, расстояние между точками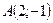 
и 
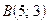равно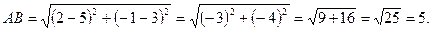 
Координаты точки 
– середины отрезка AB равны полусуммам одноименных координат, т.е., если и , то 
(7)
Например, точка M – середина отрезка AB, если A(2;-1) и B(5;3), имеет координаты: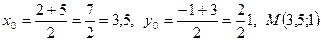 
.
Общее уравнение прямой: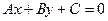 
. (8)
Уравнение прямой, проходящей через две данные точки и имеет вид: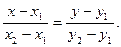 
(9)
Например, уравнение прямой, проходящей через точки A(2;-1) и B(5;3), запишется:
Уравнение прямой с угловым коэффициентом: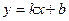 
(10),
где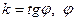 
– угол наклона прямой к положительному направлению оси абсцисс.
Уравнение с угловым коэффициентом (10) получается из общего уравнения (8), если из него выразить y:
.
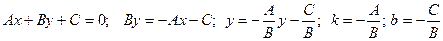Например, полученное выше общее уравнение прямой AB: 
, запишется уравнением с угловым коэффициентом: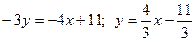 
.
Уравнение прямой, проходящей через данную точку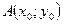 
в данном направлении: 
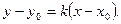(11)
Точка пересечения двух прямых 
и 
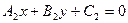находится как решение системы двух линейных уравнений:
.
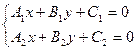Угол α между двумя прямыми определяется через угловые коэффициенты этих прямых по формуле:
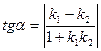, (12)
Где 
и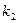 
– угловые коэффициенты данных прямых.
Две прямые параллельны, если 
, перпендикулярны, если 
, т.е. 
. (13)
Вектор – это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если A – начало вектора, а B – его конец, то вектор обозначается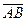 
.
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты его начала. Т.е., если и , то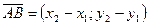 
. (14)
Например, если A(2;-3) и B(5;1), то 
.
Длиной вектора 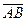называется длина отрезка AB и обозначается 
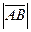. Длину вектора 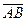вычисляют по формуле:
(15)
Например, длина вектор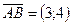а 
равна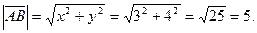 
Скалярным произведением вектора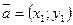 
и вектора 
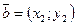называется число, равное:
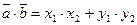(16)
Например, скалярное произведение векторов 
и 
равно: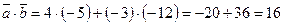 
.
Угол между векторам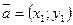и и 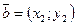задается формулой: 
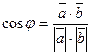. (17)
Например, найдем угол между векторам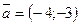и 
и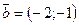 
. Для этого найдем сначала длину каждого вектора: 
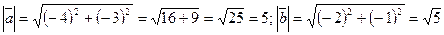Затем найдем скалярное произведение этих векторов: 
Тогда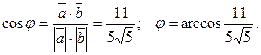 
Пример. Даны вершины треугольника ABC: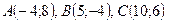 
. Найти: 1) уравнение прямой AB; 2) уравнение высоты CD и ее длину; 3) координаты векторов 
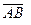и 
; 4) угол A треугольника ABC.
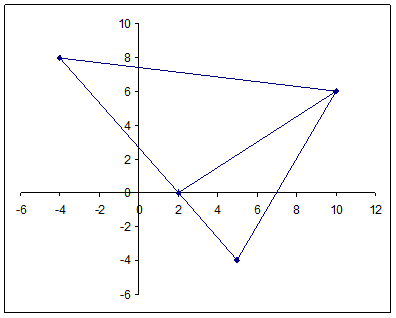Решение. Выполним чертеж к задаче (рис. 1)
y
A
C
D x
 |
B Рис. 1
1) Уравнение прямой AB запишем по формуле (9):
т.к. 
то примем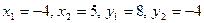 
и получим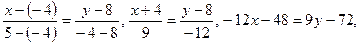 
Выразим y: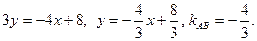 
2) Составим уравнение высоты CD. Т.к.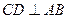 
, то ее угловой коэффициент: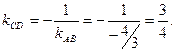 
Уравнение CD запишем по формуле (11):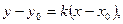 
т.к. она проходит через точку 
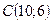в направлении, заданном угловым коэффициентом 
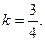Получим: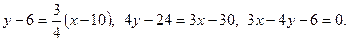 
Чтобы найти длину высоты CD, необходимо знать координаты точки D. Найдем их, решив систему уравнений:
Координаты точки D(2; 0). Длину высоты CD найдем как расстояние между точками и D по формуле (6): 
3) Координаты векторов 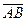и 
по формуле (14):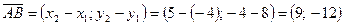 
,
.
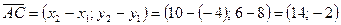4) Угол A треугольника ABC можно найти как угол между векторами 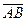и по формуле (17). Для этого найдем длины этих векторов (15) и их скалярные произведения (16):
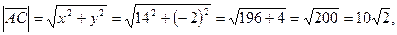
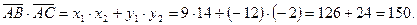
Ответ. 1) Уравнение стороны AB: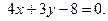 
2) Уравнение высоты CD: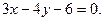 
Ее длина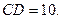 
3) 
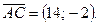
4) Угол между векторами и равен 
.
