Линейным уравнением называется уравнение вида
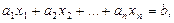
где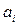 
и b – числа, 
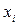- неизвестные.
Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.
Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.
Системой линейных уравнений (линейной системой) называется система вида
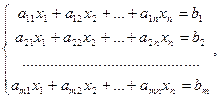(1)
где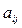 
, 
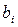- числа, 
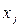- неизвестные, n – число неизвестных, m – число уравнений.
Решением линейной системы называется набор чисел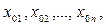 
которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.
Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная линейная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Т.е. систему уравнений (1)
приводят к эквивалентной системе
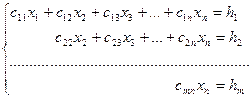
Преобразования Гаусса удобно проводить не с самими уравнениями, а с их коэффициентами в матричной форме, используя расширенную матрицу:
.
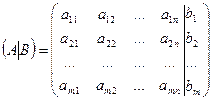Пример. Решить методом Гаусса системы линейных уравнений.
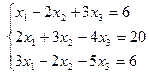
Преобразования Гаусса проведем над расширенной матрицей.
Прямой ход.
~ 
– ~
~ 
~ 
~
~ 
.
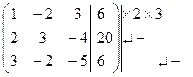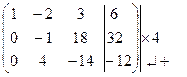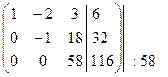Обратный ход. Перейдем к системе уравнений.
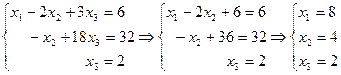
Проверка. 8 – 8 + 6 = 6 (верно), 16 + 12 – 8 = 20 (верно),
24 – 8 – 10 = 6 (верно).
Ответ.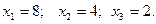 
Правило Крамера
Рассмотрим линейную систему, в которой число уравнений равно числу неизвестных: (1)
Назовем главным определителем такой системы определитель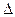 
, элементами которого являются коэффициенты при неизвестных:
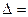
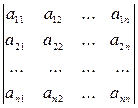, (2)
а определителем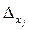 
- определитель, полученный из (2) заменой столбца коэффициентов при xj на столбец свободных членов. Тогда:
1) Если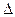 
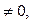система (1) имеет единственное решение, определяемое по формулам: 
.
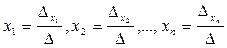2) Если 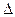= =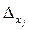0, система имеет бесконечно много решений.
3) Если 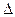= 0, а хотя бы один из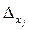 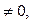система не имеет решений.
Пример.
Решить систему по правилу Крамера: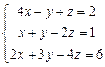 
.
Главный определитель
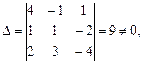
следовательно, система имеет единственное решение.
Найдем Δ х, Δ у и Δ z:
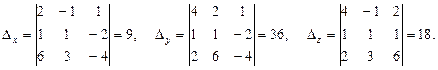
Отсюда
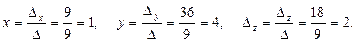
Решение линейных систем с помощью обратной матрицы
Рассмотрим линейную систему (1) и введем следующие обозначения:
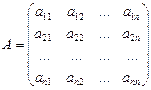- матрица системы, 
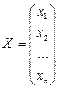- столбец неизвестных,
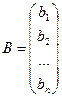- столбец свободных членов. Тогда систему (1) можно записать в виде матричного уравнения: АХ = В. (3)
Если матрица A – невырожденная (ее определитель отличен от нуля), то она имеет обратную матрицу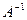 
, причем 
.
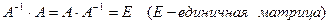Пусть матрица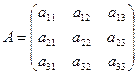 
– невырожденная, тогда
.
Умножим обе части равенства (3) слева на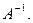 
Получим
Но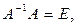 
тогда 
, а поскольку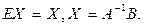 
Итак, решением матричного уравнения (3) является произведение матрицы, обратной к А, на столбец свободных членов системы (1).
Пример.
Решить систему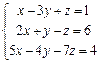 
с помощью обратной матрицы.
Составим матрицу системы:
.
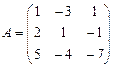Δ А = -51 ≠ 0, следовательно, система имеет единственное решение.
Найдем матрицу А -1:
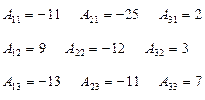
Тогда 
.
Если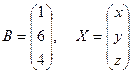 
, то исходная система превращается в матричное уравнение АХ = В, решение которого
Х = А -1 В. Следовательно,
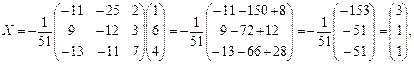
то есть х = 3, у = 1, z = 1.
