Суммой матриц А и В одинаковой размерности m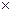 
n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: 
Например, найти сумму матриц 
и 
.
Вычислим элементы матрицы С = А + В, складывая элементы исходных матриц, стоящие на одинаковых местах:
Следовательно,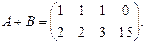 
Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.
Например, найти матрицу 5 А – 2 В, если 
.
.
Итак, 5 А – 2 В 
.
Произведением матрицы А размерности m 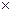p и матрицы В размерности 
называется матрица С размерности 
, каждый элемент которой 
определяется формулой: 
Таким образом, элемент представляет собой сумму произведений элементов i -й cтроки матрицы А на соответствующие элементы j -го столбца матрицы В.
Операция перемножения матриц некоммутативна, т.е.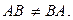 
Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей. Если существуют и АВ, и ВА, то они могут иметь разные размерности (если 
).
Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.
Например, в ыясним, можно ли умножить друг на друга матрицы
и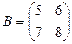 
.
Если произведение существует, вычислить его.
Сравним размерности матриц А и В: A [3×2], B [2×2]. Следовательно,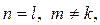 
поэтому произведение АВ [3×2] существует, а произведение ВА – нет.
Найдем элементы АВ:
(ab)11 = 0 · 5 + 3 · 7 = 21; (ab)12 = 0 · 6 + 3 · 8 = 24;
(ab)21 = 4 · 5 – 2 · 7 = 6;
(ab)22 = 4 · 6 – 2 · 8 = 8; (ab)31 = 1 · 5 – 1 · 7 = -2;
(ab)32 = 1 · 6 – 1 · 8 = -2.
Таким образом, 
, ВА не существует.
Методические указания к задаче № 3
Ранг матрицы
Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы. Таким образом, каждый элемент матрицы является ее минором 1-го порядка.
Ранг матрицы – это порядок ее наибольшего ненулевого минора (обозначения: r(A), R(A), Rang A).
Пример.
Определить ранг матрицы
.
Единственным минором максимального (3-го) порядка для матрицы А является ее определитель. Если Δ А ≠ 0, r (A) = 3; если Δ А = 0, r (A) < 3.
Найдем Δ А разложением по первой строке:
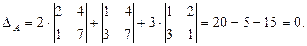
Следовательно, r (A) < 3. Поскольку матрица А содержит ненулевые элементы, r (A) > 0. Значит, r (A) = 1 или r (A) = 2. Если найдется минор 2-го порядка, не равный нулю, то r (A) = 2.
Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:
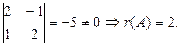
Для матриц большой размерности непосредственное вычисление всех миноров затруднительно. Поэтому в этом случае можно преобразовать матрицу к так называемому треугольному виду (когда элементы, стоящие ниже 
равны 0), воспользовавшись операциями, не изменяющими ранг матрицы (эквивалентными преобразованиями). К ним относятся:
1) транспонирование;
2) умножение строки на ненулевое число;
3) перестановка строк;
4) прибавление к элементам данной строки элементов любой другой строки, умноженных на ненулевое число;
5) вычеркивание нулевой строки.
Действительно, любая из этих операций переводит нулевые миноры в нулевые, а ненулевые – в ненулевые. Матрица, полученная в результате, не равна исходной, но имеет тот же ранг.
Пример.
Определить ранг матрицы
.
У матрицы А существуют миноры до 4-го порядка включительно, поэтому r (A) ≤ 4. Разумеется, непосредственное вычисление всех миноров 4-го, 3-го и т.д. порядка потребовало бы слишком много времени. Поэтому, используя элементарные преобразования, приведем матрицу А к треугольному виду. Поменяем местами 1-ю и 2-ю строки, чтобы элемент а 11 стал равным 1:
А ~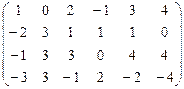 
.
Прибавим к третьей строке первую, ко второй – удвоенную первую, к четвертой – первую, умноженную на 3. Тогда все элементы 1-го столбца, кроме а 11, окажутся равными нулю:
А ~ 
.
Вычтем вторую строку полученной матрицы из третьей и четвертой строк:
А ~ 
и вычеркнем нулевые строки:
А ~ 
.
Итак, ранг матрицы А равен рангу полученной матрицы размера 2×6, т.е.
r (A) ≤ 2. Минор
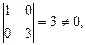
следовательно, r (A) = 2.
