Основные правила и требования
Каждый студент выполняет один вариант задания. Выбор варианта осуществляется по номеру в журнале группы или по указанию преподавателя. Преподаватель также определяет какие задачи должен решить каждый студент.
Сроки сдачи задания устанавливаются преподавателем.
Варианты заданий
а) Дана расширенная матрица системы. Найти решение этой системы и
соответствующей ей однородной системы.
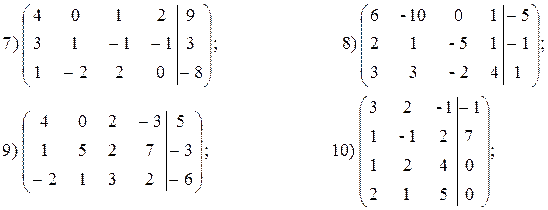
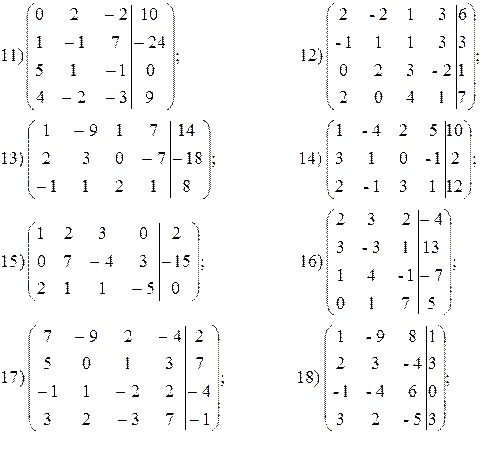
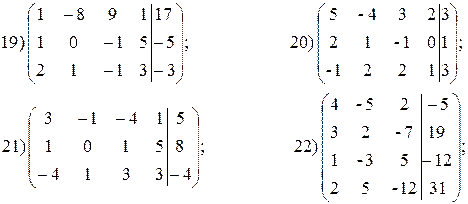
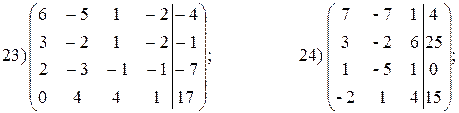
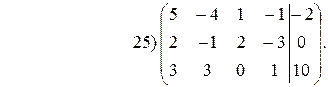
б) Дана прямая Ах + Ву + С = 0. Составить уравнение прямой, проходящей через заданную точку М 0
Параллельно данной прямой;
2) перпендикулярно данной прямой.
Исходные данные взять из табл.1.
Таблица 1
| № вари- анта | А | В | С | М 0 | А 1 | В 1 | С 1 | D 1 | А 2 | В 2 | С 2 | D 2 | М 1 |
| -2 | 3;-1 | -3 | -18 | -1 | -1 | -2 | 1;1;0 | ||||||
| -2;3 | -2 | -1 | 1;0;2 | ||||||||||
| -4 | 7;5 | -26 | -3 | -2 | -5 | 0;0;1 | |||||||
| 2;3 | -5 | 2;1;-1 | |||||||||||
| -3;7 | -2 | -3 | -1 | 1;2;2 | |||||||||
| -2 | 4;5 | -2 | 2;3;5 | ||||||||||
| 1;-2 | -2 | -3 | 1;-1;-1 | ||||||||||
| 2;-1 | -2 | -2 | 2;3;-1 | ||||||||||
| 3;-2 | -3 | -2 | -2 | 1;-5;3 | |||||||||
| 0;10 | -1 | -1 | -22 | -1 | -10 | -7;5;9 | |||||||
| 5;-5 | -3 | -3;2;5 | |||||||||||
| -3 | -3 | 1;-7 | -2 | -5 | -2 | -4 | 3;-4;-6 | ||||||
| -3 | -9;1 | -1 | -3 | -1 | -5 | 2;5;7 | |||||||
| -3 | 3;4 | -7 | 0;0;5 | ||||||||||
| 4;2 | -1 | -5 | -4 | 3;-2;0 | |||||||||
| -1 | 7;0 | -3 | -1 | -1 | -9 | -2 | 7;0;3; | ||||||
| -4 | 1;-2 | -2 | -1 | -3;60 | |||||||||
| -3 | 2;8 | -6 | -6 | -1 | 4;0;0 | ||||||||
| 1;3 | -1 | -4 | -5 | -2 | -4 | 3;0;4 | |||||||
| 4;-5 | -5 | -4 | -2 | -4 | 0;5;1 | ||||||||
| -1 | 0;0 | -2 | 0;0;0 | ||||||||||
| -15 | 1;1 | -1 | -1 | -6 | 1;2;2 | ||||||||
| -2 | -13 | 1;-2 | -2 | -1 | -2 | -1 | -1 | 2;3;-1 | |||||
| 2;-3 | -1 | -3 | -2 | 3;-5;7 | |||||||||
| -7 | -2;1 | -3 | -1 | 2;4;-6 |
в) Для матрицы третьего порядка вычислить ее определитель; найти ее обратную матрицу; найти собственные значения и собственные вектора:
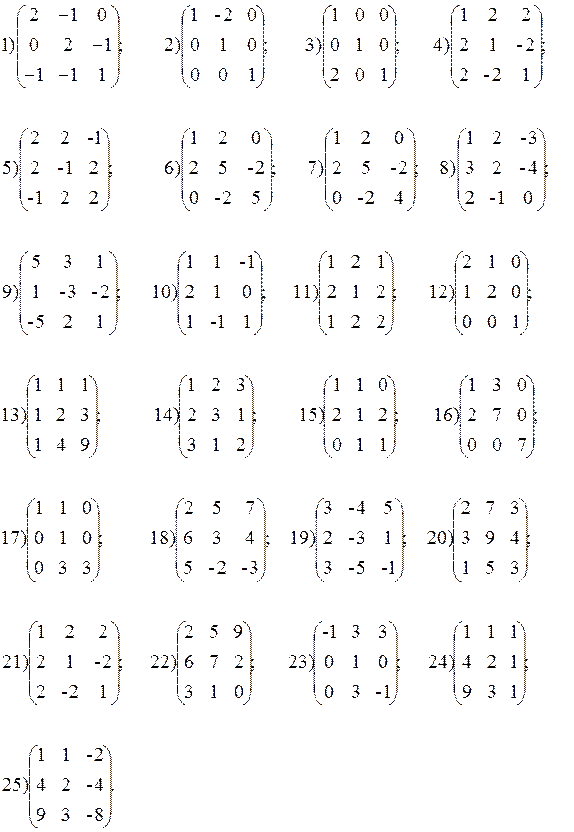
г) Найти определитель четвертого порядка:
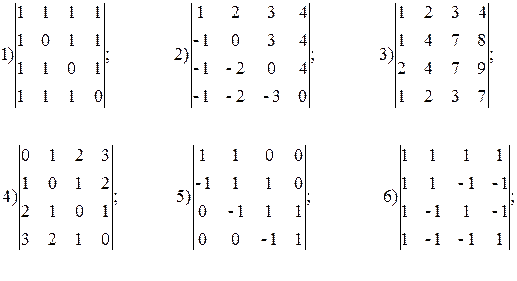
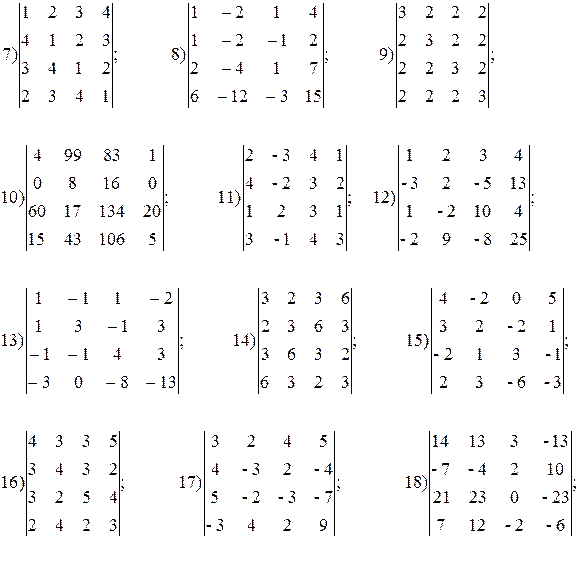
д) Для прямых Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 найти их взаимное расположение. В случае их пересечения найти угол между ними, в случае их параллельности - расстояние. Исходные данные взять из
табл. 1.
е) Даны вершины треугольника с координатами (А, А 1), (В, В 1) и
(С, С 1). Найти уравнения высоты и медианы этого треугольника (на ваш выбор). Исходные данные взять из табл. 1.
ж) Вычислить расстояние от точки М 1 до плоскости
А 1 х + В 1 у + С 1 z + D 1 = 0. Исходные данные взять из табл. 1.
з) Найти угол между плоскостями А 1 х + В 1 у + С 1 z + D 1 = 0 и
А 2 х + В 2 у + С 2 z + D 2 = 0. Исходные данные взять из табл. 1.
и) Найти точку Q, симметричную точке М 1 относительно прямой
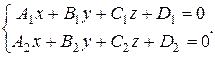
Исходные данные взять из табл. 1.
к) Написать уравнение прямой, проходящей через точки (x 0, y 0, z 0) и P. Исходные данные взять из табл. 2.
л) Вычислить расстояние d от точки Р до прямой
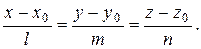Исходные данные взять в табл. 2.
м) По координатам вершин пирамиды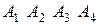 
найти: 1) длины ребер 
и 
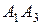; 2) угол между ребрами и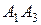 
; 3) площадь грани 
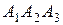; 4) объем пирамиды; 5) уравнение прямых и ;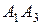
6) уравнения плоскостей 
и 
; 7) угол между плоскостями и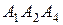 
;
1. 
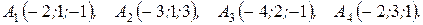
2. 
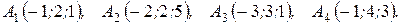
3. 
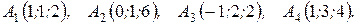
4. 
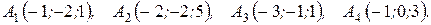
5. 
6. 
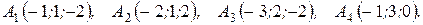
7. 
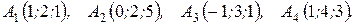
8. 
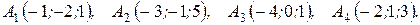
9. 
10. 
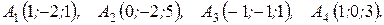
11. 
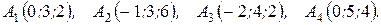
12. 
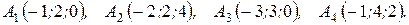
13. 
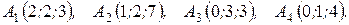
15. 
16. 
17. 
18. 
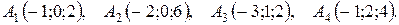
19. 
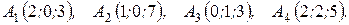
20. 
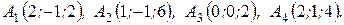
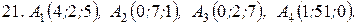
22. 
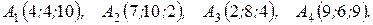
23. 
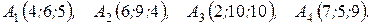
24. 
25. 
Таблица 2
| № варианта- | (x 0, y 0, z 0) | (l,m,n) | P | № варианта | (x 0, y 0, z 0) | (l,m,n) | P |
| 1;-1;7 | 2;-3;3 | 1;2;-3 | 1;-1;0 | 1;-2;6 | 1;0;-1 | ||
| -5;2;-3; | 3;-2;-1 | 1;-2;5 | -2;1;3 | -2;3;2 | 4;3;0 | ||
| -3;-2;8 | 3;2;-2 | -1;1;0 | 2;-1;5 | 3;-4;4 | 2;1;0 | ||
| -7;5;9 | 3;-1;4 | 2;0;-2 | 5;-3;5 | -2;2;-1 | 3;0;-1 | ||
| 1;-2;5 | 2;-3;4 | 0;2;3 | -2;0;1 | 2;-3;4 | 3;1;7 | ||
| 7;2;1 | 3;2;-2 | 0;2;3 | 3;-2;0 | 1;-1;2 | 1;2;-7 | ||
| 5;6;-3 | 13;1;-4 | 3;-4;-2 | 0;1;0 | 1;-2;3 | 3;3;5 | ||
| 2;3;-3 | 2;-3;2 | 0;0;0 | 3;2;-6 | 2;3;-4 | 5;-1;-4 | ||
| -4;4;-1 | 2;-1;-2 | 3;3;1 | 5;-1;-4 | 1;-4;1 | 3;2;-6 | ||
| -5;5;5 | 4;-3;-5 | 1;0;2 | 1;-2;1 | 2;3;-6 | 0;5;6 | ||
| 2;-4;1 | 3;-2;2 | 3;-2;-4 | 3;5;-2 | -4;3;-12 | 2;2;3 | ||
| 5;-3;-1 | 2;-4;3 | 4;2;-1 | 1;-1;3 | 3;2-5 | -1;2;-3 | ||
| 9;0;2 | 6;-2;-1 | -5;-5;1 |
н) Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
| 1. | 1)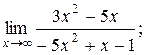 
| 2)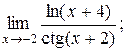 
|
3) 
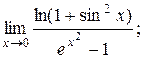
| 4)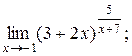 
| |
| 2. | 1) 
| 2)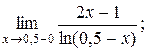 
|
3) 
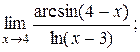
| 4)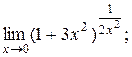 
| |
| 3. | 1)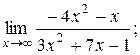 
| 2)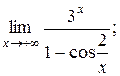 
|
3) 
| 4)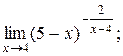 
| |
| 4. | 1)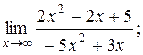 
| 2) 
|
3) 
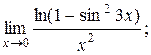
| 4) 
| |
| 5. | 1) 
| 2)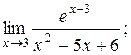 
|
3) 
| 4)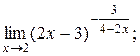 
| |
| 6. | 1) 
| 2)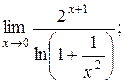 
|
3) 
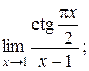
| 4)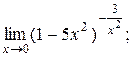 
| |
| 7. | 1)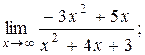 
| 2)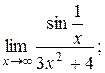 
|
3) 
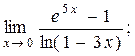
| 4) 
| |
| 8. | 1)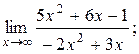 
| 2)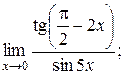 
|
3) 
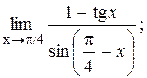
| 4)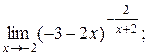 
| |
| 9. | 1)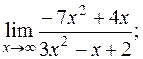 
| 2) 
|
3) 
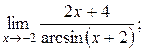
| 4)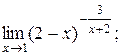 
| |
| 10. | 1)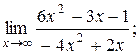 
| 2)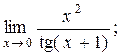 
|
3) 
| 4) 
| |
| 11. | 1) 
| 2)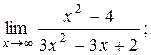 
|
3) 
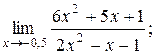
| 4)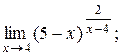 
| |
| 12. | 1)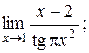 
| 2)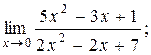 
|
3) 
| 4)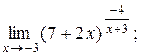 
| |
| 13. | 1)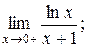 
| 2)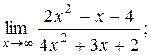 
|
3) 
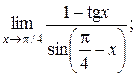
| 4)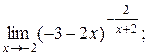
| |
| 14. | 1)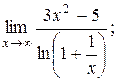 
| 2)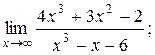 
|
3) 
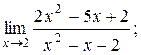
| 4)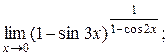 
| |
| 15. | 1)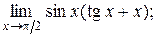 
| 2)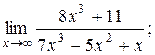 
|
3) 
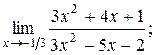
| 4)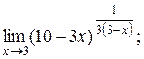 
|
| 16. | 1)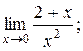 
| 2) 
|
3) 
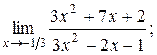
| 4)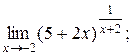 
| |
| 17. | 1)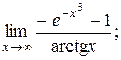 
| 2) 
|
3) 
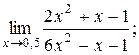
| 4) 
| |
| 18. | 1)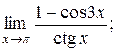 
| 2)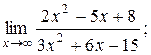 
|
3) 
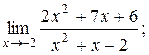
| 4)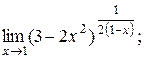 
| |
| 19. | 1) 
| 2)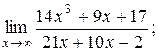 
|
3) 
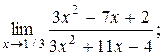
| 4)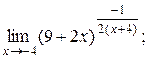 
| |
| 20. | 1) 
| 2) 
|
3) 
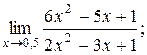
| 4)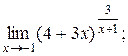 
| |
| 21. | 1) 
| 2)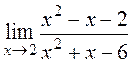 
|
3) 
| 4)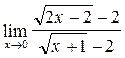 
|
| 22. | 1)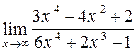 
| 2)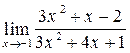 
|
3) 
| 4)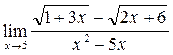 
| |
| 23. | 1)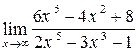 
| 2) 
|
3) 
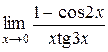
| 4) 
| |
| 24. | 1)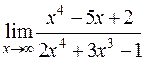 
| 2) 
|
3) 
| 4) 
| |
| 25. | 1) 
| 2)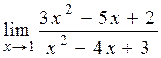 
|
3) 
| 4)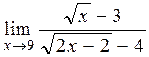 
|
о) Исследовать функцию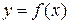 
на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.
1. 
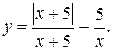
| 2.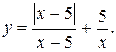 
|
3. 
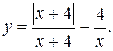
| 4.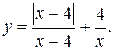 
|
5. 
| 6.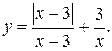 
|
7. 
| 8.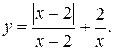 
|
9. 
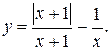
| 10.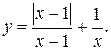 
|
11. 
| 12.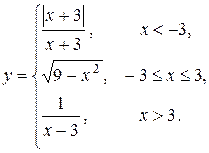 
|
13. 
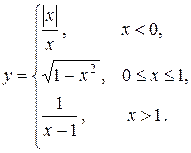
| 14. 
|
15. 
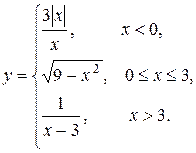
| 16. 
|
17. 
| 18.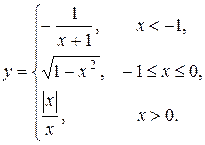 
|
19. 
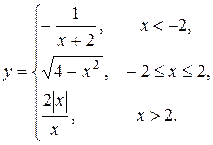
| 20.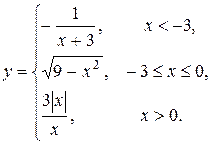 
|
21. 
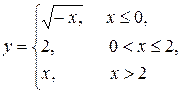
| 22. 
|
23. 
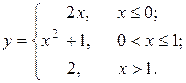
| 24.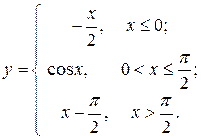 
|
25. 
|
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
1. Данко П.Е., Попов А.Г., Кожевников Т.Л. Высшая математика в упражнениях и задачах.Ч.1.- М.: Высшая школа, 1986.- 304 с.
2. Сборник задач по математике для втузов/ Под ред. А.В.Ефимова, Б.П.Демидовича.- М.: Наука, 1981.- 464 с.
