ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ
Определители второго порядка
Определителем второго порядка 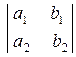 называется число:
называется число:
 .
.
Определение показывает несложность вычисления определителей второго порядка.
Примеры. 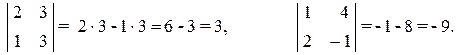
Определители третьего порядка
Определителем третьего порядка  называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:
называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:
 .
.
Примеры.
а)  -
-
-15-24-24=0
б)

Определители произвольного порядка
Пусть задан определитель n-го порядка
 .
.
Для любого определителя выполнены свойства:
а) если в определителе две строки или два столбца равны, то определитель равен нулю:

б) если в определителе какая-либо строка или столбец состоит из нулей, то этот определитель равен нулю:

в) общий множитель в строке или столбце можно вынести за знак определителя:
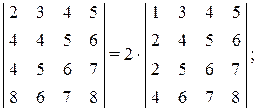
г) если в определителе поменять местами две строки или два столбца, то определитель изменит знак:
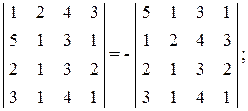
д) определитель не изменится, если к произвольной строке прибавить другую строку, домноженную на любое число. Это же справедливо и для столбцов. Например, в следующем определителе к третьей строке добавлена первая, домноженная на минус два:

Для вычисления определителей специального треугольного вида применимо следующее правило:
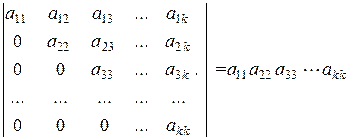 .
.
Свойства определителей позволяют любой определитель свести к треугольному виду и вычислить его по указанному правилу.
Примеры.
а)  (ко второй строке прибавляем первую, домноженную на (-2), к третьей строке прибавляем первую, домноженную на (-3), к четвертой строке прибавляем первую, домноженную на (-8))
(ко второй строке прибавляем первую, домноженную на (-2), к третьей строке прибавляем первую, домноженную на (-3), к четвертой строке прибавляем первую, домноженную на (-8))
 (к третьей строке прибавляем вторую, домноженную на (-2))
(к третьей строке прибавляем вторую, домноженную на (-2))
 (по второму свойству определителей).
(по второму свойству определителей).
б)  (поменяем вторую и первую строки местами, чтобы иметь единицу на первом месте в первой строке) =
(поменяем вторую и первую строки местами, чтобы иметь единицу на первом месте в первой строке) =
 (ко второй строке прибавляем первую, домноженную на (-3) и т.д.) =
(ко второй строке прибавляем первую, домноженную на (-3) и т.д.) =
 .
.
в)  (к третьей строке прибавляем вторую, домноженную на (-1), к четвертой строке прибавляем третью, домноженную на (-1), для уменьшения чисел в первом столбце)
(к третьей строке прибавляем вторую, домноженную на (-1), к четвертой строке прибавляем третью, домноженную на (-1), для уменьшения чисел в первом столбце)

МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ
Понятие матрицы
Матрицей порядка n ´ m называется прямоугольная таблица чисел вида
 .
.
Числа аij называются элементами матрицы. Матрицу будем коротко записывать  = (аij) n ´ m . Если n=m, то матрица называется квадратной порядка n.
= (аij) n ´ m . Если n=m, то матрица называется квадратной порядка n.
Матрица 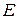 с элементами
с элементами 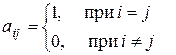 (i,j =1,2,…, n) называется единичной матрицей n- го порядка.
(i,j =1,2,…, n) называется единичной матрицей n- го порядка.
Умножение матрицы на число
Чтобы умножить матрицу А на число l, необходимо умножить каждый элемент матрицы на это число.
Пример. Для матрицы  найдем произведение
найдем произведение  . Из определения получаем
. Из определения получаем 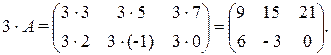
Сложение матриц
Если матрица В = (bij) n ´ m имеет тот же порядок, что и матрица А = =(аij) n ´ m , то можно определить их сумму - матрицу С = А + В = (cij)n´m того же порядка - по правилу: сij = аij + bij для i =1, 2,..., n; j = 1, 2,..., m. Матрицы различных порядков складывать нельзя.
Пример. Найдем сумму матриц А + В, где

Умножение матриц
Произведением матрицы А = (аij) n´m на матрицу В = (bij) m ´ p называется матрица С = А´ В = (сij) n ´ p, построенная по правилу

Практически перемножение матриц осуществляется следующим образом: берут i- ю строку матрицы А, умножают ее поэлементно на j -й столбец матрицы В и эти произведения складывают. Полученное число является элементом матрицы С, стоящим в i -й строке и j- м столбце.
Пример. Найдем произведение матриц АВ, если

Внимание:
а) матрица А имеет порядок n ´ m, матрица В имеет порядок m ´ p, а их произведение АВ - порядок n ´ p;
б) в общем случае АВ ¹ ВА.
Примеры.
а) Найдем ВА, где матрицы А и В взяты из предыдущего примера:

б) Найдем значение матричного многочлена В = 2 А 2 + 3 А + 5 Е, где
 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Имеем
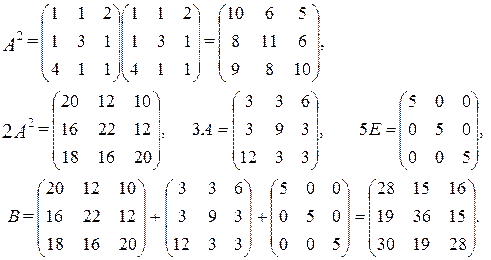 тогда
тогда
Обратная матрица
Для квадратной матрицы А порядка n можно определить такую матрицу Х порядка n, что ХА = АХ = Е, где Е - единичная матрица порядка n.
Матрица Х называется обратной к матрице А и обозначается А -1.
Следующие условия являются необходимыми и достаточными, чтобы у матрицы А = (аij) n ´ m была определена обратная матрица:
а) n=m;
б) определитель матрицы А не равняется нулю:

Следующие преобразования строк матрицы называются элементарными:
а) умножение любой строки на число, отличное от нуля;
б) прибавление к строке другой строки, домноженной на любое число;
в) перестановка строк;
г) отбрасывание нулевой строки.
Для нахождения обратной матрицы А -1 применяется следующее правило:
а) выписывается матрица
 (2.1)
(2.1)
б) с помощью элементарных преобразований над строками матрицы (2.1) превращают ее левую половину в единичную матрицу. Тогда ее правая половина превращается в обратную к ней матрицу А -1.
Примеры.
а) Для матрицы  найдем обратную.
найдем обратную.
По приведенному выше правилу получаем:

Итак, обратная матрица А -1 равна

б) Решим матричное уравнение ХА + В = С, где
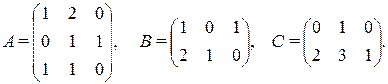
Умножим уравнение справа (порядок важен) на матрицу А -1. Тогда
ХАА -1 + ВА -1 = СА- 1. Так как АА -1 = Е, то ХЕ + ВА -1 = СА -1 или
 = СА -1- - ВА -1 =(С-В)А -1.
= СА -1- - ВА -1 =(С-В)А -1.
Найдем разность матриц

Вычислим матрицу А -1

Тогда Х = (С-В)А -1 = 
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ






