В термодинамических неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. Теплопроводность представляет собой перенос энергии: если в одной области газа кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит выравнивание средних кинетических энергий молекул, т. е. выравнивание температуры газа по всему объему.
Распространение теплоты в газах происходит тремя способами: тепловым излучением (перенос энергии электромагнитными волнами), конвекцией (перенос энергии за счет перемещения слоев газа в пространстве из области с более высокой температурой в области с низкой температурой) и теплопроводностью.
Теплопроводность подчиняется закону Фурье (система отсчета выбрана так, что ось х ориентирована в направлении переноса):
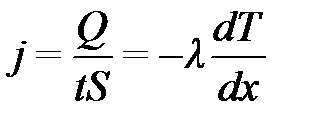 ,
,
где j – плотность теплового потока (энергия, переносимая в единицу времени через единичную площадку перпендикулярно оси х); λ – коэффициент теплопроводности; dT / dx – градиент температуры вдоль оси x; знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры.
Для идеального газа коэффициент теплопроводности определяется по формуле:
 ,
,
где ρ – плотность газа; <ℓ> – средняя длина свободного пробега молекулы; < v T> – средняя скорость теплового движения молекул; c V – удельная теплоемкость газа при постоянном объеме.
Средняя скорость теплового движения молекул:
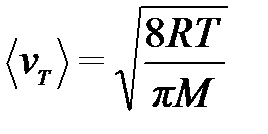 ,
,
где М – молярная масса.
Рассмотрим два коаксиальных цилиндра, пространство между которыми заполнено газом. Если внутренний цилиндр нагревать, а температуру наружного цилиндра поддерживать постоянной, ниже температуры нагревателя, то в газе между цилиндрами возникает радиальный поток теплоты, направленный от внутреннего цилиндра к наружному. При этом температура слоев газа, прилегающих к стенкам цилиндров, равна температуре стенок. Выделим в газе цилиндрический слой радиусом r, толщиной dr и длиной L. По закону Фурье количество теплоты, которое проходит через этот слой за одну секунду, выражается формулой:
 .
.
Отсюда:
 .
.
Тогда:
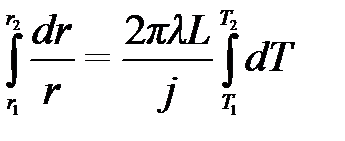 ,
,
где T 1 и r 1, T 2 и r 2 – соответственно температуры поверхностей и радиусы внутреннего и наружного цилиндров.
Таким образом, процесс теплопроводности от нити к окружающей ее цилиндрической поверхности описывается уравнением:
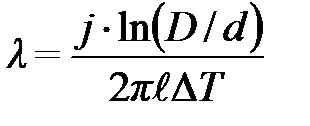 , (1)
, (1)
где λ – коэффициент теплопроводности; j – плотность теплового потока (мощность на единицу площади); D – внутренний диаметр трубки; d – диаметр нити, ℓ – длина нити; Δ T – разность температур нити и трубки.
В установке ФПТ-1-3 тепловой поток создается вольфрамовой нитью при нагревании постоянным током. Сопротивление нити при повышении температуры значительно изменяется, поэтому его измерение осуществляется сравнением падений напряжения на нити и на эталонном резисторе, включенном последовательно с нитью. Тепловой поток определяется по формуле:
 , (2)
, (2)
где I – сила тока в нити, R н – сопротивление нити, U н – падение напряжения на нити; U р –падение напряжения на эталонном резисторе; R p – сопротивление эталонного резистора (R p= 41 Ом).
Разность температур нити и трубки:
 ,
,
где Т н – температура нити; Т т – температура трубки, равная температуре окружающего воздуха.
Температура трубки в процессе эксперимента принимается постоянной, т. к. поверхность обдувается с помощью вентилятора потоком воздуха. Температура нити тем выше, чем больше протекающий по ней ток.
Разность температур по результатам измерений падений напряжения можно определить с помощью выражения:
 , (3)
, (3)
где U н– падение напряжение нити в нагретом состоянии; U н0 – падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10 мА); U р – падение напряжение на эталоном резисторе при нагретой нити; U р0 – падение напряжения на эталонном резисторе при холодной нити; α – температурный коэффициент сопротивления; t – температура воздуха в градусах Цельсия.




