Рівнянням (9), тобто законом Фур’є в прямій формі не можливо скористатись не знаючи закону розподілу температури в середовищі, а відповідно величини градієнту температури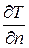 
. Відповідь на це питання дає диференційне рівняння теплопровідності, яке виводиться з рівняння теплового балансу і рівняння Фур’є, що розглядаються в межах елементарного об’єму 
.
В кінцевій формі (вивід є в рекомендованій літературі) рівняння приймає вигляд
(11)
де 
- коефіцієнт температуропроводності, 
, 
, 
вже відомі нам коефіцієнт теплопровідності, теплоємність і густина речовини.
Величини 
характеризує тепло інерційні властивості тіла. Із збільшенням зміна температури (
) в часі також зростає.
Вираз 
називають оператор Лапласа.
Для випадку, коли температура змінюється тільки в одному напрямку (називається одномірною задачею), рівняння(11) спрощується
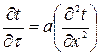(12)
Рівняння (11) ще більше спрощується для стаціонарного процесу, коли 
. Оскільки фізична константа 
, то рівняння (11) остаточно приймає вигляд
(13)
Це рівняння слід розв’язувати при заданих граничних умовах.
Розглянемо конкретну задачу – теплопровідність плоскої стінки.
Граничними умовами є
x=0 t=tст.1 (14)
x= 
t=tст.2 (15)
Після інтегрування (13) враховуючи, що в даному випадку часткова похідна співпадає з повною отримаємо
(16) 
(17)
Підставляючи граничні умови (14) та (15) в рівняння (16) і (17) отримаємо рівняння, яке визначає градієнт температури
(18)
і рівняння, яке називається рівнянням теплопровідності плоскої стінки (19)
(19)
або
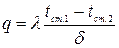(20)
Рівняння (19) і (20) дозволяють визначити кількість тепла Q і тепловий потік q для випадку теплопровідності плоскої стінки в стаціонарних умовах.
Якщо рівняння (20) представити у вигляді
і порівняти його із законом Ома, що визначає силу струму
, де 
- різниця потенціалів (або рушійна сила), R – опір провідника, то видно їх тотожність. За аналогією знаменник 
називають термічним опором стінки (
). Якщо стінка складається з декількох шарів, наприклад, стальний апарат емальований зсередини, а зовні покритий тепловою ізоляцією, то опори сумуються (як при послідовному з’єднанні провідників)
(21)
В цьому випадку рівняння теплопровідності плоскої стінки (21) буде мати вигляд
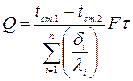(22)
Якщо стінка має циліндричну форму (трубопроводи, покриті тепловою ізоляцією) при співвідношенні 
, розподіл температури по товщині стінки буде підпорядковуватись вже не лінійному, а логарифмічному закону (в зв’язку з тим, що тепловий потік – постійна величина, а поверхня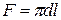 
- змінюється із зміною 
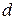), рівняння теплопровідності циліндричної стінки отримає вигляд
(23)
Для багатошарової стінки:
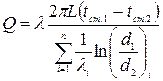(24)
де 
- коефіцієнт теплопровідності 
-го шару, 
- співвідношення 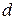цього шару.
