Линейным однородным ДУ второго порядка с постоянными коэффициентами называется уравнение вида
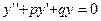или 
, (10.1)
где 
- постоянные величины.
Для отыскания общего решения уравнения (10.1) составляется характеристическое уравнение
, (10.2)
Которое получается из уравнения (10.1) замено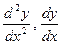й 
и 
на соответствующие степени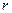 
, причём сама функция заменяется единицей.
При решении уравнения (10.2) возможны три случая.
I случай. Корни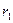 
и 
– действительные и различные. В этом случае общее решение уравнения (10.1) имеет вид: 
.
II случай. Корни 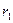и – действительные и равные: 
. В этом случае общее решение уравнения (10.1) имеет вид: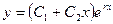 
.
III случай. Корн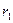и и – комплексно-сопряжённые: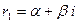 
; 
. В этом случае общее решение уравнения (*) имеет вид: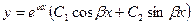 
.
1. Решить уравнения:
а)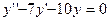 
.
Решение. Составим характеристическое уравнение и найдём его корни:
Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения согласно первому случаю запишется так:
.
б) 
.
Решение. Составим характеристическое уравнение и найдём его корни:
Так как корни характеристического уравнения действительные и равные, то общее решение данного дифференциального уравнения согласно второму случаю запишется так:
.
в) 
.
Решение. Составим характеристическое уравнение и найдём его корни:
Так как корни характеристического уравнения комплексно-сопряжённые, то общее решение данного дифференциального уравнения согласно третьему случаю запишется так:
.
Тема 11.Решение задач с помощью кругов Эйлера
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
1.В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение
Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно,
25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:
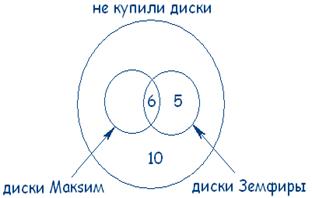
Ответ: 6 покупателей купили диски и Максим, и Земфиры
2. В группе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение:
М- множество студентов, пользующихся метро
А- множество студентов, пользующихся автобусом
Т- множество студентов, пользующихся троллейбусом
U- множество студентов группы
m(U) = 30
m(M) =20
m(А) = 15
m(Т) =23
m(М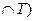 
= 10
m (М 
= 12
m (Т = 9
m (М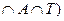 
=?
Для решения опять воспользуемся кругами Эйлера.
Пусть х человек пользуется всеми тремя видами транспорта.
Тогда пользуются только метро и троллейбусом (10–х) человек,
только автобусом и троллейбусом (9–х) человек, только метро и автобусом (12–х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.Аналогично получаем: (х – 6) ч. – только автобусом, (х + 4) ч. – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
