Уравнение вида
, (5.1)
где 
и 
- заданные функции от х, в частности – постоянные.
Уравнение вида 
, где 
, 
, 
, (5.2)
называется уравнением Бернулли.
На практике ДУ удобнее искать методом Бернулли в виде 
.
Метод Бернулли. ДУ (5.2) ищется в виде произведения двух других функций, т.е. с помощью подстановки , где u и v неизвестные функции от х. Тогда 
. Подставляя выражения 
и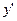 
в уравнение (5.2), получаем
(5.3)
или 
. (5.4)
Далее приравниваем выражение в скобках к нулю и решаем ДУ 
. Итак, получили ДУ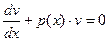 
- уравнение с разделяющимися переменными. Решив последнее уравнение, получим 
.
Подставляя найденную функцию 
в уравнение (5.3), получаем
.
Определив u, возвращаемся к переменной .
Найдите общее решение линейного ДУ первого порядка: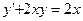 
.
Решение. Сделав замены и 
, получим 
.
Сгруппируем второе слагаемое с третьим:
Приравнивая к нулю выражение в скобках, находим функцию :
Подставив в уравнение (7.2), находим 
:
Найдём интеграл методом замены:
.
Получим, что 
.
Итак, общее решение данного уравнения есть 
.
2. Найдите общее решение уравнения Бернулли: 
.
Решение. Сделав замены и , получим 
.
Сгруппируем второе слагаемое с третьим:
Приравнивая к нулю выражение в скобках, находим функцию :
Подставив в уравнение (8.4), находим :
Отсюда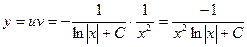 
.
Тема 6.Решение однородных дифференциальных уравнений
Функция 
называется однородной функцией n-го порядка, если при умножении каждого её аргумента на произвольный множитель 
вся функция умножится на 
, т.е. 
.
Дифференциальное уравнение 
(9) называется однородным, если функция есть однородная функция нулевого порядка.
С помощью замены 
, где u – новая неизвестная функция, уравнение сводится к уравнению с разделяющимися переменными.
1. Найдите общее решение ДУ 
Решение. Сравнивая уравнение с общим видом ДУ , имеем 
. Так как 
, то является однородным уравнением. Сделав замену и 
, получим
Получили уравнение с разделяющимися переменными.
Сделав обратную замену 
, получим общее решение
Тема 7. Нахождение частных производных и полного дифференциала функций
Частной производной от функции 
по переменной х называется производная этой функции при постоянном значении переменной у и обозначается 
или 
.
Частной производной от функции по переменной у называется производная этой функции при постоянном значении переменной х и обозначается 
или 
.
Полным дифференциалом функции в некоторой точке 
называется выражение
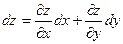, (7.1)
где и вычисляются в точке , а 
, 
.
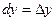1. Найдите частные производные функций:
а)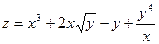 
; б) 
.
Решение.
а) При вычислении переменная у считается как постоянная величина:
.
При вычислении переменная х считается как постоянная величина:
.
б) При вычислении переменная у считается как постоянная величина и имеем произведение двух функций, зависящих от х, поэтому применяем правило вычисления производных: 
:
При вычислении переменная х считается как постоянная величина:
.
2. Найдите полный дифференциал функции 
в точке М (1; 2).
Решение. Находим частные производные:
;
.
Вычислим значения частных производных в точке М (1; 2):
;
.
Согласно формуле (7.1.), получим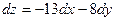 
.
