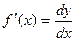ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.
Дисциплина: Математика
Специальность: 23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта», А-4107
| № п/п | Содержание самостоятельной работы |
| 1. | Производные функций. Дифференциалы функций |
| 2. | Дифференцирование функций |
| 3. | Нахождение дифференциала функции |
| 4. | Интегрирование функции |
| 5. | Решение линейных дифференциальных уравнений первого порядка и уравнений Бернулли |
| 6. | Решение однородных дифференциальных уравнений |
| 7. | Нахождение частных производных и полного дифференциала функций |
| 8. | Решение уравнений в полных дифференциалах |
| 9. | Решение дифференциальных уравнений высших порядков |
| 10. | Решение дифференциальных линейных однородных уравнений с постоянными коэффициентами |
| 11. | Решение задач с помощью кругов Эйлера |
| 12. | Погрешности приближённых значений чисел |
| 13. | Действия над приближёнными значениями чисел |
| 14. | Решение задач на вычисление вероятностей случайных событий |
| 15. | Решение задач на вычисление вероятностей при повторных испытаниях |
| 16. | Выборка и её представление |
Литература
Основная
1. Миронова Н.П. Теория вероятностей и математическая статистика. – Ростов н/Д.: Феникс, 2012. – 212 с.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2013. – 479 с.
3. Гончаров Г.А. Элементы дискретной математики. – М.: ФОРУМ: ИНФРА-М, 2012. – 128 с.
4. Практические занятия по математике. Учебное пособие для средних проф. учеб. заведений/Н.В. Богомолов. – М.: Высшая школа, 2013. – 495 с.
5. Пискунов Н.С. Дифференциальные и интегральные исчисления, Т.1,2 – М.: Наука, 2012. -416 с.
Дополнительная
1. Спирин П.А. Теория вероятностей и математическая статистика / М.С. Спирина. – М.: Академия, 2013. – 352 с.
2. Спирин П.А. Дискретная математика/ М.С. Спирина. – М.: Академия, 2012. – 368 с.
3. Матвеев П.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям: Учеб. пособие, 7-е изд., доп. СПб.: "Лань", 2012. 432 с.
Тема 1. Производные функций. Дифференциалы функций.
Производной функции 
в точке 
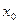называется предел отношения приращения функции в этой точке 
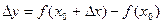к приращению аргумента 
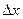при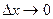 
, если этот предел существует:
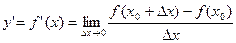. (1.1)
Функция 
, имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Для производной функции употребляются следующие обозначения: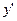 
, 
, 
, 
.
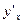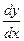Нахождение производной называется дифференцированием.
Правила дифференцирования:
1. 
;
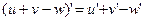2. 
;
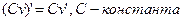3. 
;
4. 
.
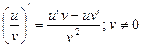Таблица основных производных:
Таблица 1
|
|
|
| |
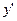
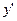
| С-постоянная |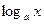 
| 
| ||
| 
| 
| 
| |
| 
|
| 
| |
| 
| 
| ||
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| -
| |
|
| 
| 
| |
|
| 
| -
|
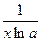
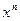
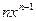
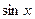
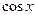
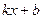
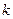
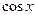
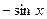
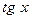
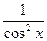
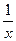
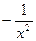
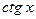
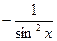
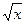
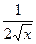
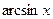
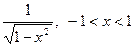
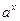
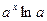
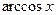
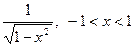
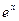
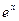
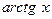
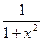
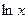
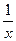
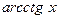
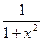
Производной второго порядка функции называется производная от её производной, т.е.
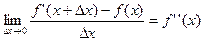. (1.2)
Производную от второй производной называют производной третьего порядка.
В общем случае производной n-го порядка называется производная от производной (n-1)-го порядка: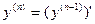 
.
Пусть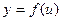 
и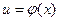 
, тогда 
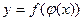– сложная функция с промежуточным аргументом u и независимым аргументом x.
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу:
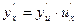. (1.3)
1.Найдём производную функции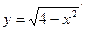 
, используя формулу (1.3). Данная функция не является элементарной. Полагая 
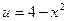, получим 
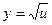. Находим 
.
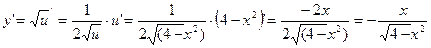Производная в точке. Для вычисления производной функции в точке 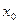нужно в выражение производной вместо переменной подставить значение 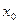. В итоге должно получиться число.
Производная высшего порядка. Производные второго, третьего и более высоких порядков вычисляются последовательным дифференцированием данной функции.
Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx.
Можно также записать: 
