У математиці існує ряд загальних методів доведення теорем. Розглянемо деякі з них.
Дедуктивне доведення. Це основний метод математичних доведень. Кожен його крок ґрунтується на певному логічному законі, аксіомі або даних теорем, і все доведення є ланцюжок логічних умовиводів. При такому доведенні з правильних умов теореми ми з необхідністю дістаємо правильний висновок.
Наприклад, теорема: «Якщо число ділиться на 2 і на 3, то, оскільки воно ділиться на 2 і не ділиться на 6, воно не ділиться на 3».
Введемо позначення: А- «число ділиться на 2», В – «число ділиться на 3», С – «число ділиться на 6».
Доведення цієї теореми запишемо за допомогою послідовних дедуктивних умовиводів.
1) А, В – умова теореми;
2) А 
В;
3) А В 
С;
4) (А В С) (А 
);
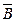5) (А 
).
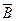На третьому кроці використано теорему: якщо число ділиться на кожне з двох взаємно простих чисел, то воно ділиться і на їхній добуток.
Повна індукція. Термін «індукція» походить від латинського induktio – наведення. У математиці використовуються повна й неповна індукції.
Доведення методом повної індукції полягає в розгляді всіх окремих випадків (чисел, фігур тощо), при яких теорема правильна. Кількість таких випадків повинна бути скінченною і невеликою за кількістю.
Теорема: Значення виразу с = а2 + b 2, (а, b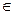 
Z) є число, що при діленні на 4 не має остачі 3.
Доведення теореми проведемо, розглядаючи три випадки: 1) обидва числа парні; 2) обидва числа непарні; 3) одне число парне, друге – непарне.
Нехай а, b – парні, тобто а = 2 m, b = 2 n, m, n 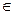Z. Дістанемо
с = (2 m)2 + (2 n)2 = 4 m 2 + 4 n 2 = 4∙ (m 2 + n 2), тобто с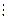 
4, остача 0.
Нехай а, b – непарні числа, тобто а = 2 m + 1, b = 2 n + 1, m, n 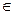Z. Маємо
с = (2 m + 1)2 + (2 n + 1)2 = 4 m 2 + 4 m + 1 + 4 n 2 + 4n + 1= 4 (m 2 + n 2 + m + n) + 2,
а це означає, що при ділені с на 4 дістанемо остачу 2, а не 3.
Випадок 3) спробуйте розглянути самостійно.
Непрямі доведення.
Зведення до абсурду. Цей метод полягає в тому, що в теоремі А В припускають, що правильним буде 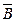. Якщо в результаті цього припущення приходять до неправильного висновку, абсурду, то роблять висновок, що наслідок В теореми А В правильний.
Цим способом доводять, наприклад, таку теорему: Якщо дві різні прямі а і b паралельні третій прямій с, то вони паралельні між собою.
Припустимо 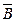, тобто а і b не паралельні. Тоді вони перетинаються в якійсь точці К, яка не належить с. Дістанемо, що через точку К поза прямою с можна провести дві прямі а і b, які паралельні с, а це суперечить аксіомі паралельності, тобто є хибним твердженням. Отже, правильним твердженням є В.
Метод від супротивного. Цей спосіб ґрунтується на законі контрапозиції А В =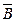 
.
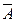Теорема: Довести, що коли аb – непарне число, то обидва множники а і b – непарні цілі числа.
Позначимо А: «добуток аb – непарне число», Т: «а – непарне число», S: «b – непарне число». Тоді теорема скорочено запишеться так:
A S T, або А В, де В «S T».
Припустимо, що =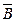 
= 
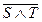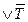, тобто один із множників а або b є парним числом. Нехай, наприклад, а – парне, тобто а = 2 m, m 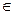Z. Тоді ab = 2mb – парне число, тоді дістали 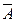. Таким чином довели теорему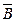 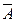, а цим самим і дану теорему А В.
Поширеним прикладом неправильних міркувань є непродумане використання неповної індукції, коли загальний висновок зроблено на основі окремих спостережень, експериментів, розгляду скінченної кількості їх. Використання неповної індукції може привести як до правильних, так і неправильних висновків. Так, побудувавши кілька графіків лінійних рівнянь з двома змінними в прямокутній системі координат і побачивши, що вони є прямими лініями, робимо висновок, що графік кожного лінійного рівняння з двома змінними є пряма лінія. Цей умовивід – правильний. Прикладом, коли неповна індукція приводить до хибного результату є теорема Ферма. Ще у XVII ст. математик П. Ферма (1601 – 1665) помітив, що числа виду Fn =22n+1 при n = 0, 1, 2, 3, 4 – прості: F0 = 3, F1 = 5, F2 = 17, F3 = 257, F4 = 65537.
Ферма висловив припущення, що при будь-якому n 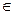N числа такого виду є простими (їх стали називати простими числами Ферма). Ця гіпотеза була висловлена на основі кількох обчислювальних експериментів. У 1732 р. видатний математик Л. Ейлер (1707 – 1783) показав, що при n = 5
F5 = 4294967297 = 641 ∙ 6700417, тобто F5 не є простим числом. Цей контрприклад спростував гіпотезу Ферма.
