Неопределённый интеграл и его свойства. Таблица основных неопределённых интегралов. Основные методы интегрирования: замена переменных, интегрирование по частям. Определенный интеграл, его геометрические и экономические приложения. Определённый интеграл как предел интегральной суммы. Формула Ньютона-Лейбница. Свойства определённого интеграла. Вычисление определённого интеграла Приближенное вычисление определенных интегралов. Геометрические и физические приложения определённого интеграла. Несобственные интегралы.
Тема 6. Дифференциальные уравнения.
Дифференциальные уравнения 1 порядка. Теорема о существовании и единственности решения. Дифференциальные уравнения с разделяющимися переменными. Однородные и линейные дифференциальные уравнения. Линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами, однородные и неоднородные
Рекомендуемая литература
Основная:
4. Кремер Н.Ш. Высшая математика для экономистов, М.: ЮНИТИ, 2001.
5. В.А. Абчук. Математика для менеджеров и экономистов. СПб.:Изд-во Михайлова В.А., 2002 г.
6. В. И. Ермаков Сборник задач по высшей математике для экономистов. М.,ИНФРА-М, 2004.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., ВШ., 2003.
8. Гмурман В. Е. Теория вероятностей и математическая статистика. М., ВШ., 2003.
1. Дополнительная:
2. М.С.Красс, Б.П.Чупрынов, Основы математики и ее приложения в экономическом образовании, М.:Дело, 2001.
3. Шипачев B.C. Основы высшей математики. М.: Высшая школа, 2001.
4. Шипачев B.C. Задачник по высшей математике. М.: Высшая школа, 2001.
Примерные контрольные работы по разделам.
Раздел 1. Линейная алгебра
Тема №1 Алгебра матриц, тема №2 Определители квадратных матриц,
Тема №3 Системы линейных алгебраических уравнений (СЛАУ).
Задача 1. Даны матрицы А и В. Найти матрицу С.
Задача 2. Найти произведение матриц А × В.
Задача 3. Решить систему линейных уравнений:
1) методом Крамера;
2) методом обратной матрицы;
3) методом Гаусса.
Задача 4. Вычислить определитель.
Задача 5. Найти ранг матрицы
.
ВАРИАНТ 1
1.  ,
,  ,
,  2.
2.  ,
, 
3  4.
4.  5.
5. 
ВАРИАНТ 2
1.  ,
,  ,
,  2.
2.  ,
, 
3.  4.
4.  5.
5. 
Тема №4 Векторная алгебра. Тема №5 Элементы аналитической геометрии.
1. Составить уравнение прямой, проходящей через точки:
Вариант 1: А(-5;4) и В(3;-2)
Вариант 2: А(1;-3) и В(2;6)
2. Через точку А провести прямые параллельно и перпендикулярно данной прямой.
Вариант 1: А(-3;4) и уравнение прямой 
Вариант 2: А(2;-1) и уравнение прямой 
3. Найти координаты центра и радиус окружности:
Вариант 1: 
Вариант 2: 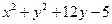
4. Найти угол между прямыми, заданными в декартовой системе координат.
Вариант 1: 2x + 5y + 4z = 0
–x + 2y – 3z = 0
Вариант 2: x – 6y – 4z = 0
3x + 2y + 7z = 0
5. На плоскости в прямоугольном декартовом базисе заданы ненулевые векторы а { а 1 ; а 2 } и b { b 1; b 2 }. Найти косинус угла, образованного данными векторами.
Вариант 1: a 1 = 2 a 2 = 4 b 1 = –1 b 2 = 5
Вариант 2: a 1 = 3 a 2 = –1 b 1 = 6 b 2 = 8
Раздел 2. Математический анализ.






