Классическая машина Атвуда (английский физик, математик, шахматист XVIII века) представляет собой установку высотой около 2-х метров, на которой два одинаковых тяжелых груза массой m (около 0.5 кг) каждый, связаны нитью, перекинутой через легкий блок При помещении на один из грузов небольшого грузика - перегрузка Δ m << m грузы начинают двигаться с небольшим ускорением, так что время движения груза можно достаточно точно измерить ручным секундомером. За счет малого момента инерции блока (J<<mr2) динамика грузов оказывается простой и соответствует классической теоретической задаче: движении двух грузов на блоке, когда ускорение системы грузов связан; с массами соотношением
. При этом также не учитывается трение в оси блока, для уменьшения которого Атвудом были предпринять: специальные усилия. Это позволяет, измеряя массы грузов, перегрузка и ускорение грузов вычислить ускорение свободного падения.
В данной установке (рис.1) массы грузов и их перемещение существенно меньше, что делает установку более компактной и безопасной. При массе перегрузка 10 г ускорение грузов массой около 100 г оказывается достаточно большим, а время движения грузов достаточно малым. Для регистрации с необходимой точностью времени движения грузов использован оптоэлектрический датчик, подключаемый к компьютеру. Таким образом, датчик и компьютером с необходимым программным обеспечением являются неотъемлемой частью установки. С их помощью измеряются интервалы времени, соответствующие перекрыванию инфракрасного луча датчика непрозрачными секторами смонтированной на блоке крыльчатки.
Рис.1
Использование компьютера позволяет не только измерить время движения груза от пуска до остановки, но и получить в одном эксперименте закон движения (зависимость координаты от времени).
Компьютер позволяет изменить и процедуру измерения ускорения, не понижая точности. В классической машине Атвуда для измерения ускорения требуется обязательно начать измерение времени t в момент начала движения груза, чтобы пройденный путь s был связан с ускорением соотношением, позволяющим
Рассчитать а по измеренным значениям s и t. В данной работе ускорение а определяется путем компьютерного подбора (по методу наименьших квадратов) коэффициентов
уравнения, наилучшим образом описывающего экспериментальную
зависимость s(t) при равноускоренном движении грузов с начальной скоростью:
Такой способ позволяет упростить процедуру запуска, и определять ускорение независимо от скорости v0- в момент начала регистрации времени
(момент первого перекрывания пучка оптоэлектрического датчика границей непрозрачного сектора на блоке).
Для упрощения ручного запуска и автоматического фиксирования нити в вертикальном положении, в нижней части установке предусмотрено «место старта» легкого груза. В конце движения разогнавшийся легкий груз тормозится в верхней части установки демпфирующим устройством (рис.1). Для удобства извлечения наборного груза из демпфирующего устройства на центральном стержне наборных грузов имеются фиксирующие резиновые кольца.
Теоретическая часть.
В работе изучается система из двух грузов на нити, перекинутых через блок, обладающий массой и моментом инерции J (рис. 1).
Рис.1
Во время движения после освобождения груза т к аждый из грузов на нити движется под действием силы тяжести (m1g и m2g, соответственно) и силы натяжения нити. Когда блок имеет массу, сила натяжения нитей справа и слева от него различна. Момент сил Т2 и T1 сообщает блоку угловое
Ускорение β кроме того, в оси блока может быть трение, и момент сил трения тормозит вращение блока.
Учет всех этих факторов приводит к следующим трем уравнениям, вытекающим из второго закона Ньютона, записанного в проекциях на ось Y в применении к двум грузам и учитывающего моменты сил Т2 и T1 относительно оси блока радиуса г для описания вращательного движения блока:
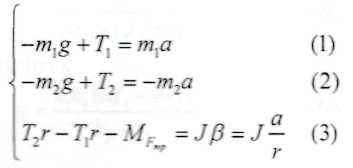
Здесь MFmp - момент силы трения. J - момент инерции блока. β - угловое ускорение блока, связанное с линейным ускорением грузов и
Нити соотношением β = a / r
Решая систему уравнений, можно получить:
Вводя значения массы перегрузка Δт = (т2-т]) и суммарной массы грузов М = (т1+т2) получим:
При отсутствии силы трения в оси (MFmp =0) и невесомом блоке (J<<Mr2). выражение (4) приобретает простой вид
Такое ускорение при движении по прямой имел бы груз с массой равной суммарной массе грузов на блоке М под действием силы, равной силе тяжести перегрузка Δmg.
При отсутствии силы трения в оси блоке ускорение грузов прямо пропорционального массе перегрузка Δm и тем меньше, чем больше суммарная масса грузов и момент инерции блока:
График зависимости ускорения грузов от массы перегрузка а(Δт) должен в этом случае представлять собой прямую, идущую в начало координат с осями а и Δm. При наличии силы трения в блоке график также представляет
собой прямую линию с тем же угловым коэффициентом 
,
однако проходящую правее начала координат и отсекающий на оси Δm отрезок, показывающий при какой массе перегрузка грузы будут двигаться равномерно (а=0).
Если измерить угловые коэффициенты k1 и к2 для двух графиков a1(Δm) и а2(Δт), полученных при разной суммарной массе грузов на нити М1 и М2, то можно вычислить ускорение свободного падения g. Действительно из двух уравнений
Можно исключить J и получить
