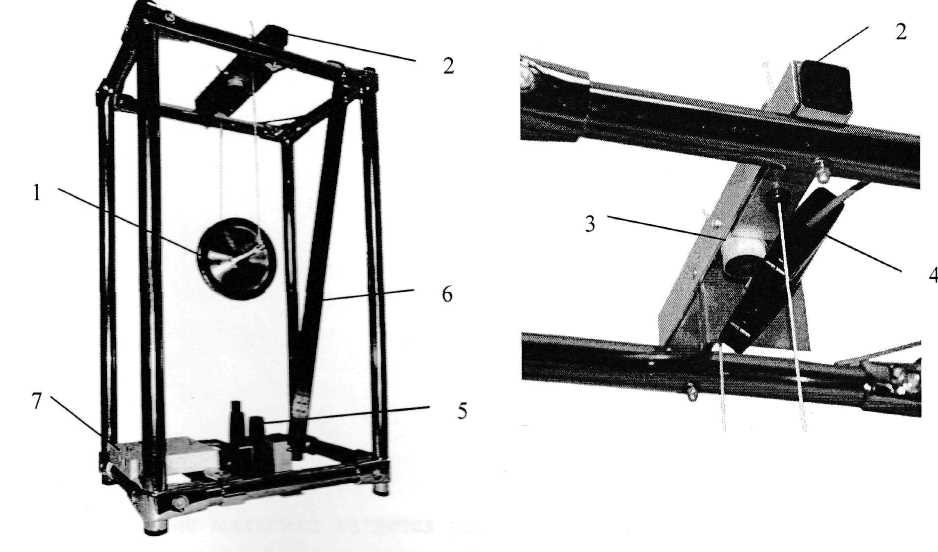
| Рис. 1 |
Маятник Максвелла представляет собой диск, неподвижно установленный на оси. На концах оси симметрично относительно диска закрепляются нити, с помощью которых маятник подвешивается к неподвижной конструкции. При вращении оси нити могут наматываться на ось или разматываться, обеспечивая тем самым перемещение маятника вверх и вниз. Если, намотав нити на ось, поднять маятник на некоторую высоту и отпустить его, то он начнет совершать колебательное движение в поле силы тяжести. В нижней точке маятник приобретает наибольшую скорость
вращения, и, продолжая вращаться по инерции, снова поднимается на некоторую высоту за счет наматывания нитей на ось. После достижения верхней точки, где скорость вращения маятника становится равной нулю, он начинает движение вниз, изменяя при этом направление вращения.
Лабораторная установка (рис. 1) включает диск маятника 1 подвешенный к верхней горизонтальной перекладине 2, винты регулирования длины нитей подвеса, а также пусковое устройство 3 на основе электромагнита и блок питания.
К приборам и принадлежностям относятся верхний оптоэлектрический датчик 4, нижний оптоэлектрический датчик 5, поворотная линейка 6, электронный блок установки 7 и компьютер с необходимым программным обеспечением.
Оптоэлектрические датчики используются для фиксации моментов времени начала движения и прихода диска на определенную высоту вблизи нижней точки траектории. Поворотная линейка служит для измерения перемещения оси вращения диска при движении от верхней точки до точки, в которой срабатывает нижний оптоэлектрический датчик. Линейка фиксируется в нерабочем положении с помощью постоянного магнита.
Теоретическая часть
Схема сил, действующих на ось маятника, показана на рис. 2. Движение маятника осуществляется под действием силы тяжести mg и силы натяжения нитей N.

Рис. 2
Движение маятника является равноускоренным до тех пор, пока нити хотя бы частично намотаны на вал. При этом угловая скорость О) вращения
диска вокруг оси и линейная скорость v геометрической оси диска связаны между собой соотношением:
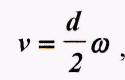 (1)
(1)
где d - диаметр вала. Иными словами, скорость движения центра масс маятника равна скорости сматывания нитей с вала. Кинетическая энергия диска равна:
 (2)
(2)
где J -момент инерции маятника.
В соответствии с законом сохранения энергии при движении в поле силы тяжести кинетическая энергия маятника, который опустился с высоты h, равна его потенциальной энергии на этой высоте, поэтому можно записать:

(3)
При равноускоренном движении скорость v выражается через высоту падения h и время движения t на основании кинематических соотношений:
 (4)
(4)
где а- ускорение, с которым движется центр масс диска. Из формул (4) следует
 (5)
(5)
Подставив (5) в уравнение (3) и решив его относительно J, получим расчетную формулу для определения момента инерции маятника Максвелла относительно его оси симметрии на основе данных эксперимента:
 (6)
(6)
Отметим, что эта формула также может быть получена с помощью уравнений динамики.
Для расчета момента инерции маятника Максвелла на основе его геометрических характеристик рекомендуется использовать формулу для момента инерции толстостенной трубы (7, 8), частным случаем которой является формула для момента инерции цилиндра. Ввиду того, что толщина диска не является постоянной, его следует представить как набор полых и сплошных цилиндров, для каждого из которых момент инерции рассчитывается отдельно, а затем результаты суммируются.
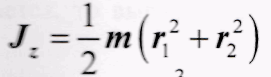 (7)
(7)
или с использованием плотности р материала:
 (8)
(8)
Обозначения для (7) и (8) приведены на рис. 3.

Рис.3
Поскольку движение маятника Максвелла во всех точках траектории кроме нижней происходит с постоянным ускорением, изменение интервала времени между уходом датчика из окрестности нижней точки и возвратом на тот же уровень может характеризовать уменьшение механической энергии маятника в процессе движения. Действительно, диск маятника в первый раз уходит с уровня h0. двигаясь вверх со скоростью v1, поднимается на высоту h1 и снова опускается на уровень h0. При следующем подъеме вверх диск проходит высоту h0. имея скорость v2, поднимается на меньшую высоту (h2) и снова опускается на уровень h0 - Время, которое диск находится выше h0 в первом случае составляет τ1 = 2 v1/a, а во втором случае равно τ2 = 2 v2/a (т.е. рассматриваемый интервал времени прямо пропорционален начальной скорости). Здесь использовано первое из соотношений (4), а множитель «2» отражает то, что при равноускоренном движении с ускорением, направленным вниз, время движения тела верх равно времени его движения вниз (т.е. полное время равно удвоенному времени движения вверх). Согласно (2).кинетическая энергия маятника пропорциональна квадрату его скорости. Поэтому относительное изменение кинетической энергии диска за один цикл движения составляет:
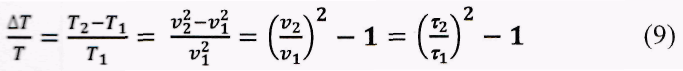
Поскольку последнее выражение содержит только интервалы времени, в течение которых диск находился выше определенного уровня, то для получения относительного изменения кинетической энергии в эксперименте достаточно измерить интервалы времени, в течение которых маятник находится выше нижнего оптоэлектрического датчика. Т.к. кинетическая энергия диска уменьшается, то выражение (9) будет иметь отрицательный знак.




