Обработка результатов измерений. 1. Определите момент инерции маятника

Таблица 2.

1. Определите момент инерции маятника. Расчет проводится по формуле (6) с использованием характеристик маятника (масса и диаметр оси с учетом толщины нити), высоты падения и времени падения. Полученный результат впишите в Таблицу 2 (J_эксп).

2. Оцените погрешность определения момента инерции на основе данных эксперимента и внесите его в таблицу.

3. Рассчитайте момент инерции маятника на основе его геометрических размеров и массы.

Внесите результаты в Таблицу 2.

4. Сопоставьте результаты расчета и эксперимента.

5. На основании данных по продолжительности первого и последующих «периодов» колебаний, рассчитайте отношения кинетической энергии, теряемой маятником за «период», к его кинетической энергии в начале колебания. Внесите результаты, полученные для нескольких циклов движения вверх-вниз, в третью строку Таблицы 1.

Указания по технике безопасности

1. Перед выполнением работы получите инструктаж у лаборанта.

2. Соблюдайте общие правила техники безопасности работы в лаборатории "Физика".

3. Перед проведением опыта проверьте целостность нитей подвеса маятника и их длину.

4. Не допускайте раскачки горизонтальных колебаний маятника, которые могут привести к ударам диска по корпусу нижнего датчика. Необходимо руками останавливать движение маятника сразу после регистрации всех необходимых данных

Контрольные вопросы

1. Опишите устройство лабораторной установки.

2. На основании рис. 2 составьте систему уравнений, описывающих движение маятника Максвелла.

3. Представьте еще один вариант разбиения использовавшегося в работе маятника на тела вращения более простой формы и обоснуйте оптимальность выбранного Вами варианта теоретического расчета момента инерции маятника.

4. Оцените погрешность теоретического расчета, связанную с упрощением реальной формы маятника.

5. Какую потенциальную энергию имеет маятник в момент перекрытия им нижнего оптоэлектрического датчика (относительно положения, когда нити полностью размотаны)? Какую часть эта энергия составляет от начальной потенциальной энергии маятника?

 

Лабораторная работа № 9

Изучение механического резонанса

Цель лабораторной работы

Изучение особенностей вынужденного колебательного движения. Построение резонансной кривой. Определение частоты резонанса.

Экспериментальное оборудование, приборы и

Принадлежности

Лабораторная установка показана на рис. 1. На основании 1, установлен блок питания 2 электродвигателя 5 с эксцентриком 4. На основании 1 укреплены также магнитная дорожка (рельс)6 с тележкой 7 на магнитной подвеске. В комплект входят две тележки одинаковой массы с разной площадью тормозящих пластин, Тележка 7 зафиксирована между двумя пружинами (9 и 10). Конец левой пружины 9 с помощью нити 12, перекинутой через блок 11, соединен с эксцентриком на маховике 4. Конец правой пружины 10 закреплен неподвижно. Передача данных в компьютер осуществляется с помощью двух USB-кабелей 15 и 14,

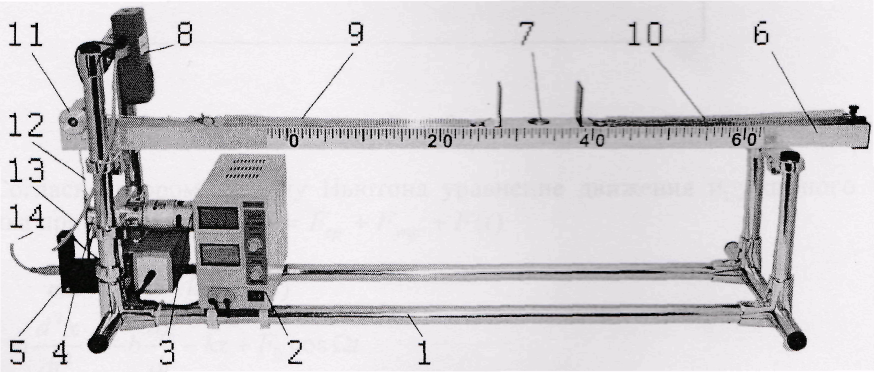
Рис. 1

К приборам и принадлежностям относятся оптоэлектрический датчик 5. контролирующий движение эксцентрика, датчик расстояния 8, а также компьютер с программным обеспечением для регистрации и обработки данных.

Теоретическая часть

3.1. Вынужденные механические колебания.

Для того чтобы в колебательной системе получить незатухающие колебания, необходимо компенсировать потери энергии, возникающие за счет сопротивления среды. Такая компенсация может быть обеспечена введением какого-либо периодически действующего фактора. В случае механических колебаний роль периодически действующего фактора играет внешняя вынуждающая сила F(t). Рассмотрим, как изменится движение пружинного маятника (рис. 2) массой m и коэффициентом жесткости пружины к (под действием силы упругости F_упр.) в среде с коэффициентом сопротивления b (сила сопротивления среды F_op пропорциональна скорости) под воздействием внешней вынуждающей силы F(t) = F₀cost, изменяющейся по гармоническому закону с частотой Ω и амплитудой F₀.

Рис. 2

Согласно второму закону Ньютона уравнение движения пружинного маятника примет вид

Тогда

или

Частное решение уравнения вынужденных колебаний, с учетом начальных условий, имеет вид

или

где начальная база

и описывает затухающие гармонические колебания пружинного маятника с начальной амплитудой А_о, начальной фазой φ, коэффициентом затухания

и частотой где частота

собственных (незатухающих) колебаний маятника.

Это решение описывает гармоническое колебания с частотой вынуждающей силы с постоянной амплитудой, но смещенное по сравнению с силой на фазу φ.

Полное решение уравнения вынужденных колебаний в зависимости от начальных условий имеет вид

или,

где амплитуда

Из этого следует, что вынужденные колебания представляют собой сумму двух колебательных движений: затухающих колебаний с частотой ω, амплитуда которых убывает по экспоненциальному закону, и незатухающих колебаний с постоянной амплитудой А и частотой вынуждающей силы Ω. Совместный вклад этих двух колебательных движений описывает сложное поведение пружинного маятника под действием внешней периодической силы, которое условно можно разбить на ряд этапов (рис. 3).

Рис.3

На первом этапе, когда затухание свободных колебаний является незначительным, наблюдается сложение двух гармонических колебаний.

Продолжительность первого этапа зависит от величины затухания Р в системе. Если коэффициент затухания достаточно велик, то данный этап может оказаться незаметным для наблюдателя.

Постепенно амплитуда свободных колебаний уменьшается и начинает оказывать меньшее влияние на движение маятника, в то время как амплитуда колебаний с частотой вынуждающей силы остается постоянной (второй этап). На первых двух этапах амплитуда колебаний маятника может меняться.

Наконец, начиная с некоторого момента времени, амплитуда затухающих колебаний становится много меньше амплитуды колебаний с частотой вынуждающей силы А_оe^βt «А (третий этап). То есть затухающие колебания перестают оказывать влияние на колебания маятника. Маятник начинает совершать гармонические колебания с постоянной амплитудой и частотой вынуждающей силы. Такие колебания называют установившимися. Первые два этапа называют периодом установления колебаний. Длительность этого периода зависит от коэффициента затухания, а также от отношения амплитуды свободных колебаний Ао и амплитуды установившихся колебаний А. Чем больше коэффициент затухания, тем быстрее наступает этап установившихся колебаний. Чем больше амплитуда свободных колебаний А, по сравнению с амплитудой установившихся колебаний А, тем процесс установления колебаний продолжительнее.

 

Явление резонанса.

Амплитуда установившихся колебаний описывается выражением:

 

 

и зависит не только от амплитуды вынуждающей силы F_o. а также зависит от частоты собственных колебаний ω₀ маятника, частоты вынуждающей силы Ω и коэффициента затухания β. Зависимость амплитуды установившихся колебаний от частоты вынуждающей силы А = А(Ω) имеет максимум (рис. 4), который соответствует минимуму подкоренного выражения. Значение частоты вынуждающей силы Ω_Р, при которой амплитуда установившихся колебаний имеет максимум, равно:

Частота Ω_р называется резонансной частотой или частотой резонанса.

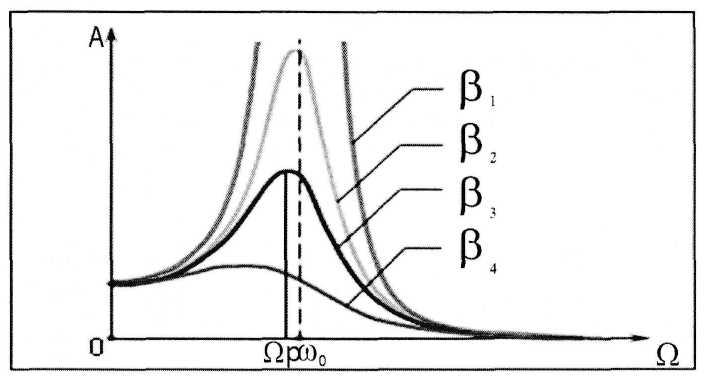
Рис. 4 (β₄>β₃>β₂>β₁)

Явление резкого возрастания амплитуды вынужденных (установившихся) колебаний при приближении частоты вынуждающей силы к частоте Ω_р называется резонансом. График зависимости амплитуды вынужденных (установившихся) колебаний от частоты вынуждающей силы А= А(Ω) называется резонансной кривой.

При малых значениях коэффициента затухания β<<ω₀резонансная частота незначительно отличается от частоты собственных колебаний Ω_р≈ω₀- С увеличением коэффициента затухания β резонансная частота Ω_р уменьшается. Максимальное значение амплитуды при этом тоже уменьшается. Максимум зависимости А = А(Ω) становится более низким и широким. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Qколебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.