1. Используя полученные результаты, определите средние значения периодов колебаний для каждой пружины как для порожней тележки массой М, так и для отягощенной грузом с общей массой М+ m.
2. Найдите средние значения жесткостей пружин из прилагаемого набора.
(<k1>и <k2>),
3. Используя правила оценки погрешностей косвенных измерений,
определите погрешности оценок ускорения свободного падения для этих
экспериментов (Δk1и Δk2).
Сравните полученные результаты.
4. Запишите окончательный результат работы в виде

где вместо <k>и Δk следует подставить полученные Вами численные значения этих величин, а δk указывает относительную погрешность Ваших измерений.
Указания по технике безопасности
1. Перед выполнением работы получите инструктаж у лаборанта.
2. Соблюдайте общие правила техники безопасности работы в лаборатории "Физика".
3. Осторожно обращайтесь с маятником. Не допускайте падений и ударов маятника.
Контрольные вопросы
1. Дайте определение периода и частоты колебаний пружинного маятника.
2. Какие колебания называются гармоническими?
3. Напишите решение дифференциального уравнения гармонических колебаний и дайте определения амплитуды, циклической частоты и фазы.
4. Сформулируйте закон Гука.
5. Выведите размерность жесткости пружины.
6. Как рассчитывается жесткость системы пружин при параллельном и последовательном их соединении?
Лабораторная работа № 7
Определение коэффициента трения скольжения.
Цель лабораторной работы
Изучить закон сухого трения и ознакомиться с методами определения коэффициента трения скольжения.
Задачи лабораторной работы
Провести экспериментальную работу по оценке кинематических параметров равноускоренного движения тела по наклонной плоскости. На основании экспериментальных данных провести расчет коэффициента трения скольжения.
Экспериментальное оборудование, приборы и принадлежности

Рис.1
Лабораторный стенд (рис.1) включает наклонную направляющую скамью 1 с прикрепленной к ней измерительной линейкой, движущееся тело 2 (2 шт.), оптоэлектрические датчики 3 (2 шт.) с модулем сбора сигналов 4, а также транспортир для измерения угла наклона направляющей скамьи.
К приборам и принадлежностям относится компьютер с необходимым программным обеспечением.
Теоретическая часть
Среди возможных сил, препятствующих движению, можно выделить одну, наиболее часто встречающуюся: силу сухого трения. Сила сухого трения представляется двумя видами: силой трения покоя, силой трения скольжения.
Сила сухого трения возникает между соприкасающимися телами и направлена по касательной к поверхности соприкосновения тел против направления движения или против силы, пытающейся вовлечь тела в движение. Необходимым условием возникновения силы сухого трения является наличие давления одного тела на поверхность другого (рис. 2 а, б,в).
Сила давления тела на опору называется весом тела. По третьему закону Ньютона ответом опоры на действие силы давления является сила
реакции опоры F реакции, которую принято представлять суммой силы нормальной реакции опоры и силы сухого трения:
Fреакции= N + Fтр (1)
Если соприкасающиеся тела неподвижны относительно друг друга, то возникающую силу сухого трения называют силой трения покоя, а при относительном перемещении тел - силой трения скольжения. Скольжение тел относительно друг друга начинается только после того, как внешняя касательная к поверхности соприкосновения тел сила (тангенциальная сила) превзойдет по размеру силу трения покоя. Таким образом, сила трения покоя изменяется от нуля до некоторого максимального значения и равна внешней силе (или ее проекции), действующей в противоположном направлении.

Рис.2
Сила трения зависит от силы давления, или прижимающей силы, материала тел и состояния поверхностей соприкосновения. У шероховатых поверхностей трение покоя больше, чем у отшлифованных.

Рис.3. График зависимости проекции силы трения на направление движения от скорости для полированных металлических поверхностей
Когда внешняя сила (тангенциальная сила) превысит размер максимальной силы трения покоя, начнется скольжение одного тела вдоль поверхности соприкосновения с другим телом. В этом случае сила трения будет направлена против вектора скорости. Ее числовое значение для хорошо отполированных металлических поверхностей при небольших скоростях практически не зависит от скорости и равно максимальной силе трения покоя. График зависимости силы трения от скорости имеет вид, изображенный на рис. 3.
Независимость силы трения от скорости соблюдается лишь при не очень больших скоростях, не для всех тел и не при всех качествах обработки поверхностей. Для других случаев график зависимости силы трения между твердыми поверхностями от скорости имеет вид, показанный на рис. 4.
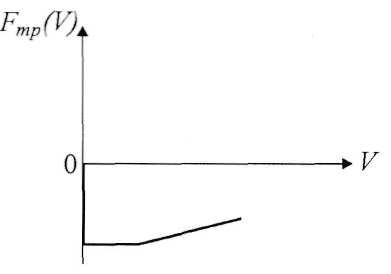
Рис.4. График зависимости проекции силы трения на направление движения от скорости для произвольных твердых поверхностей
Возникновение сухого трения обусловлено взаимодействием молекул, атомов и электронов, находящихся в поверхностных слоях трущихся друг о друга тел, т. е. в конечном счете, электромагнитным взаимодействием.
Французские физики Г.Амонтон и Ш.Кулон опытным путем установили закон трения: сила трения скольжения Fmp пропорциональна силе нормального давления Fдавл тела на опору:
 (2)
(2)
где μ - коэффициент трения, зависящий от свойств соприкасающихся тел и состояния их трущихся поверхностей.
В соответствии с III законом Ньютона Fдавл = -N, следовательно, расчет силы трения можно производить по формуле:
 (3)
(3)
Модуль силы трения скольжения определяется:
 (4)
(4)
Значение коэффициента трения скольжения μ можно получить, решив задачу о движении тела по наклонной плоскости с углом наклона α (рис. 5).

Рис.5. Схема действия сил и выбора координатных осей системы отсчета для решения задачи о соскальзывании тела с наклонной плоскости
Тело, находясь на наклонной плоскости, приходит в движение, когда проекция результирующей всех действующих на тело сил на ось х будет больше 0. В случае решения задачи со схемой действующих сил, указанной на рис. 4, движение тела начинается, когда проекция силы тяжести (mg)x будет больше размера силы трения Fmp. Следовательно, в случае равенства проекции силы тяжести на.х-ось (mg)x и силы трения тело будет либо покоиться, либо двигаться с постоянной скоростью. Тогда
0=(mg)x-Fmp (5)
или
mgsina=μN (6)
В проекции на ось у
0= - mgcosα+N (7)
При этом
N=mgcosα. (8)
Тогда подстановка значения N из (8) в уравнение (6) дает:
mg-sina—/иmg-cosa, (9)
следовательно,
μ = tga. (10)
Отсюда следует, что коэффициент трения равен тангенсу угла наклона плоскости к горизонту, при котором начинается соскальзывание тела с наклонной плоскости.
Однако установить с достаточной точностью коэффициент трения скольжения μ по экспериментальному значению предельного угла начала соскальзывания тела с наклонной плоскости довольно сложно. Поэтому в данной лабораторной работе используют метод экспериментальной оценки коэффициента трения скольжения при движении тела по наклонной плоскости с ускорением.

Рис.6
Тело, пущенное с вершины наклонной плоскости, перемещается по закону равноускоренного движения

(11)
Если на пути его движения на фиксированных расстояниях поместить оптические датчики, то времена прохождений телом соответствующих координат должны быть согласованы друг с другом в соответствии с формулой (11). Используя численный алгоритм квадратичной аппроксимации экспериментальных точек, можно найти величину ускорения а.
По значению рассчитанного ускорения, используя закон движения тела (II закон Ньютона), можно определить коэффициент трения μ. Для этого запишем II закон Ньютона для тела т (см. рис. 6):
Fmp+N + mg = ma, (12)
Выразим это уравнение в проекциях на оси х и у:
х: -Fmp+mgsinα = mat (13)
у:: N-mgcosα = 0 (14)
Сила трения тогда будет
Fmp=μN = μmgcosα (15)
Подставляя Fmp в уравнения проекции на ось х (13), получим
-μ. Mgcosα+ mgsinα - та (16)
Отсюда можно записать расчетную формулу для определения коэффициента трения μ:
 (17).
(17).
Анализ выражения (17) показывает, что для определения коэффициента трения необходимо знать угол наклона плоскости α и ускорение тела а.






