Метою методики раціонального планування експерименту є скорочення кількості дослідних даних, необхідних для отримання математичної залежності невідомої функції від декількох незалежних один від одного параметрів. Кількість незалежних параметрів не повинна бути більше 4. При більшій кількості незалежних параметрів слід звертатись до теорії подібності і розмірностей.
Незалежні параметри 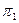 ,
,  , …,
, …,  , від яких необхідно побудувати залежність, будемо називати
, від яких необхідно побудувати залежність, будемо називати  - параметрами. Функцію
- параметрами. Функцію  , яка залежить від
, яка залежить від  - параметрів, будемо називати функцією відгуком чи просто відгуком. Лінії залежності відгуку від
- параметрів, будемо називати функцією відгуком чи просто відгуком. Лінії залежності відгуку від 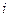 -ого
-ого  - параметра називаються лініями регресії. Побудова лінії регресії ведеться на основі дослідних даних по точках в координатах
- параметра називаються лініями регресії. Побудова лінії регресії ведеться на основі дослідних даних по точках в координатах  . При цьому кількість дослідних точок, по яких будується залежність
. При цьому кількість дослідних точок, по яких будується залежність  , будемо називати рівнями функції. Так, якщо при побудові залежності
, будемо називати рівнями функції. Так, якщо при побудові залежності  , використано 5 дослідних даних (точок), то говорять, що функція побудована по п’яти рівнях. Кількість рівней слід вибирати нечетним числом. Практика показує, що для досягнення точності функції-відгуку повинна будуватись по п’яти рівнях.
, використано 5 дослідних даних (точок), то говорять, що функція побудована по п’яти рівнях. Кількість рівней слід вибирати нечетним числом. Практика показує, що для досягнення точності функції-відгуку повинна будуватись по п’яти рівнях.
Апроксимацією даної залежності називається описом її лінії регресії математичною формулою. Апроксимація як правило виконується по методу найменших квадратів.
Метод найменших квадратів – один із методів регресійного аналізу для оцінки невідомих величин по результатах вимірювань, які містять випадкові помилки. Кожна величина, що шукається, може бути виміряна безпосередньо, як наприклад, довжина відрізку чи кут, то, для збільшення точності, вимірювання проводиться багато разів, і за кінцевий результат беруть арифметичне середнє з усіх окремих вимірювань. Це правило арифметичної середини базується на основі теорії ймовірності; легко можна показати, що сума квадратів відхилень окремих вимірювань від арифметичної середини буде менше, ніж сума квадратів відхилень окремих вимірювань від будь-якої іншої величини. Саме правило арифметичної середини являє, відповідно, найпростіший випадок методу найменших квадратів, який буде описаний нижче.
В багатьох випадках необхідно здійснити прогноз режимів роботи на певний проміжок часу по деяких параметрах. Такє прогнозування можливе за рахунок побудови математичної моделі процессу прогнозування. Знайти математичну модель дозволяє регресійний аналіз, який дозволяє графічно відображати тенденції даних і прогнозувати їх подальші зміни. Використовуючи регресійний аналіз можна здійснити прогноз за межі реальних даних для передбачення майбутніх значень і для демонстрації тенденції зміни певних параметрів.
Можна визначити плинне середнє, якє згладжує відхилення в даних і дозволяє знайти більш точну математичну модель.
Чим ближче точність апроксимації до одиниці, тим більша точність одержаної математичної моделі.
Лінійна апроксимація – це пряма лінія, яка найбільше підходить для величин, які збільшуються або зменшуються з постійною швидкістю.
Логарифмічна апроксимація корисна для опису величин, які спочатку швидко зростають або спадають, а потім поступово стабілізуються. Логарифмічна апроксимація використовує як від’ємні, так і позитивні величини.
Поліноміальна апроксимація використовується для описання величин поперемінно зростаючих і спадаючих. Вона корисна для аналізу великого набору даних про нестабільну величину. Степінь полінома визначається кількістю екстремумів (максимумів і мінімумів) кривої.
Ступенева апроксимація корисна для опису монотонно спадаючої величини. Використання ступеневої апроксимації неможливе, якщо дані містять нульові чи від’ємні значення.
Експоненціальна апроксимація застосовується в тому випадку, якщо швидкість зміни даних неперервно зростає. Однак для даних, які містять нульові чи від’ємні значення цей вид наближення неможливий.






