6.1. Понятие алгоритма и его свойства
Каждый из нас постоянно решает множество задач: как быстрее добраться на работу, как лучше спланировать дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически, так как на протяжении многих лет привыкли к их выполнению, другие требуют длительного размышления над решением, но в любом случае, решение каждой задачи всегда делится на простые действия.
Алгоритм — описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи. Понятие алгоритма, являющееся фундаментальным в математике и информатике, возникло задолго до появления средств вычислительной техники. Слово «алгоритм» появилось в средние века, когда европейцы познакомились со способами выполнения арифметических действий в десятичной системе счисления, описанными узбекским математиком Муххамедом бен Аль-Хорезми («аль-Хорезми» — человек из города Хорезми; в настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм — есть результат европейского произношения слов аль-Хорезми. Первоначально под алгоритмом понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.
Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т.д.). Свойством, характеризующим любого исполнителя, является то, что он умеет выполнять некоторые команды. Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовы  вать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
вать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Значение слова «алгоритм» очень схоже со значениями слов «рецепт», «метод», «процесс». Однако, в отличие от рецепта или процесса, алгоритм характеризуется следующими свойствами: дискретностью, массовостью, определенностью, результативностью, формальностью.
Дискретность (разрывность — противоположно непрерывности)— это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги».
Массовость — применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Например, алгоритм решения квадратного уравнения в области действительных чисел должен содержать все возможные исходы решения, т.е., рассмотрев значения дискриминанта, алгоритм находит либо два различных корня уравнения, либо два равных, либо делает вывод о том, что действительных корней нет.
Определенность (детерминированность, точность) — свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Помните сказку про Ивана-царевича? «Шел Иван-царевич по дороге, дошел до развилки. Видит большой камень, на нем надпись: «Прямо пойдешь - голову потеряешь, направо пойдешь - жену найдешь, налево пойдешь — разбогатеешь». Стоит Иван и думает, что дальше делать», Таких инструкций 'алгоритм содержать не может.
Результативность — свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Вопрос о рассмотрении бесконечных алгоритмов остается за рамками теории алгоритмов.
Формальность — это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции. Рассуждать «что, как и почему?» должен разработчик алгоритма, а исполнитель формально (не думая) поочередно исполняет предложенные команды, и получает необходимый результат.
6.2. Способы описания алгоритмов
Рассмотрим следующие способы описания алгоритма: словесное описание, псевдокод, блок-схема, программа.
Словесное описание представляет структуру алгоритма на естественном языке. Например, любой прибор бытовой техники (утюг, электропила, дрель и т.п.) имеет инструкцию по эксплуатации, т.е. словесное описания алгоритма, в соответствии которому данный прибор должен использоваться.
Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как строго не формализуем (под «формальным» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при описании некоторых действий; страдает многословностью.
Псевдокод — описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить -основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.
Строгих синтаксических правил для записи псевдокода не существует. Это облегчает запись алгоритма при проектировании и позволяет описать алгоритм, используя любой набор команд. Однако в псевдокоде обычно используются некоторые конструкции, присущие формальным языкам, что облегчает переход от псевдокода к записи алгоритма на языке программирования. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слов и конструкций.
Блок-схема — описание структуры алгоритма с помощью геометрических фигур с.линиями-связями, показывающими порядок выполнения отдельных инструкций. Этот способ имеет ряд преимуществ. Благодаря наглядности, он обеспечивает «читаемость» алгоритма и явно отображает порядок выполнения отдельных команд. В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.
Рассмотрим некоторые основные конструкции, использующиеся для построения блок-схем.

|
Блок, характеризующий начало/конец алгоритма (для1 подпрограмм — вызов/возврат):

|
Блок - процесс, предназначенный для описания отдельных действий:
 Блок — предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам):
Блок — предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам):
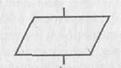 Блок — ввода/вывода с неопределенного носителя:
Блок — ввода/вывода с неопределенного носителя:
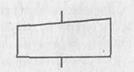 Блок — ввод с клавиатуры
Блок — ввод с клавиатуры

Блок — вывод на монитор:
 Блок — вывод на печатающее устройство:
Блок — вывод на печатающее устройство:
|

|
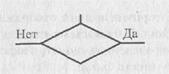
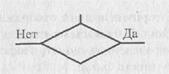
Блок — решение (проверка условия или условный блок):

|

|
 Блок, описывающий цикл с параметром:
Блок, описывающий цикл с параметром:
 Блок — границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»:
Блок — границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»:
Соединительные блоки 
Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.
Программа — описание структуры алгоритма на языке алгоритмического программирования. С другой стороны, понятие «программа» нельзя трактовать только таким образом, как уже говорилось в главе 5 (п. 5.5.2), программа на языке декларативного программирования представляет собой совокупность описанных знаний и не содержит явного алгоритма исполнения.
6.3, Основные алгоритмические конструкции
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.
6.3.1. Линейная алгоритмическая конструкция
 Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i-го действия (шага) выполняется (i-1)-е действие (шаг), если /-е действие - не конец алгоритма.
Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i-го действия (шага) выполняется (i-1)-е действие (шаг), если /-е действие - не конец алгоритма.
Пример 6.1.
Опишем алгоритм сложения двух чисел на псевдокоде в виде блок-схемы (рис. 6.1).
Псевдокод:
1. Ввод двух чисел а, Ь.
2. Вычисляем сумму S — а + b.
3. Вывод S.
4. Конец.
Рис. 6.1. Блок-схема к примеру 6.1
6.3,2, Разветвляющееся алгоритмическая конструкция
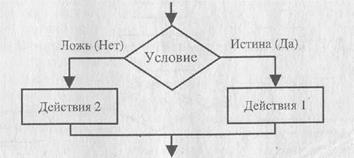 Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если — то) и полное (если — то — иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 6.2). Неполное ветвление предполагает наличие некоторых действий алгоритма только
Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если — то) и полное (если — то — иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 6.2). Неполное ветвление предполагает наличие некоторых действий алгоритма только
Рис. 6.2. Полное ветвление
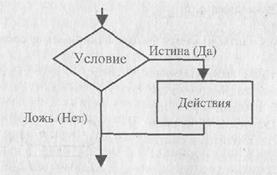
на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния (рис. 6.3).
Пример 6.2.
Вывести значение наибольшего из двух чисел. Псевдокод:
1. Ввод двух чисел а, Ь.
2. ЕСЛИ а > Ь, ТО «выводим а»,
ИНАЧЕ «выводим Ь».
3. Конец.
|
Рис. 6.3. Неполное ветвление
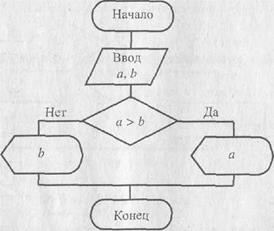
Рис. 6.4. Блок-схема к примеру 6.2
В данном примере реализовано полное ветвление. ЕСЛИ значения входных данных таковы, что а >Ь, ТО выполняется линейный алгоритм:
1. Ввод двух чисел а, Ь.
2. Вывод а.
ИНАЧЕ, когда а < Ь, выполняется линейный алгоритм:
1. Ввод двух чисел а, b.
2. Вывод b.
Вывод: алгоритм является разветвляющимся и состоит из двух
ветвей.
|
Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Основная идея алгоритма сводится к следующему: за наибольшее (наименьшее) принимаем значение любого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). Если окажется, что очередное значение входного данного боль-nie (меньше) наибольшего (наименьшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, сравнив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует неполное ветвление.
Пример 6.3.
Заданы три числа. Найти значение наименьшего из них.
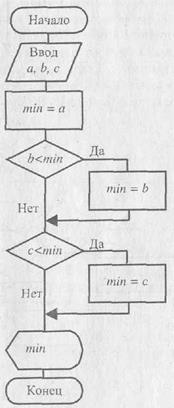
| Рис. 6.5. Алгоритм поиска наименьшего значения среди трех заданных |
Заданные числа обозначим: а, Ь, с; результирующее наименьшее - min. На рис. 6.5 представлена блок-схема алгоритма решения данной задачи.
Команда «выбор»
| Рис. 6.6. Команда «выбор» |
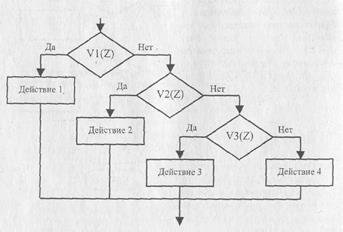 Часто при выборе одного из возможных вариантов действий приходится проверять значение выражения на принадлежность заданному набору данных. Для этого существует команда «Выбор». При ее исполнении сначала вычисляется значение некоторого выражения 2. Затем последовательно проверяются условия VI, V2,..., \п относительно Z, начиная с первого, до тех пор, пока не встретится условие, принимающее значение ИСТИНА. Далее выполняется соответствующее этому условию действие (или серия действий), после чего команда выбора завершается. Если ни одно из условий не является истинным, то выполняется действие (или набор действий), идущее по ветви ЛОЖЬ для каждого из условий. На рис. 6.6 представлена блок-схема команды «Выбор» для п = 3.
Часто при выборе одного из возможных вариантов действий приходится проверять значение выражения на принадлежность заданному набору данных. Для этого существует команда «Выбор». При ее исполнении сначала вычисляется значение некоторого выражения 2. Затем последовательно проверяются условия VI, V2,..., \п относительно Z, начиная с первого, до тех пор, пока не встретится условие, принимающее значение ИСТИНА. Далее выполняется соответствующее этому условию действие (или серия действий), после чего команда выбора завершается. Если ни одно из условий не является истинным, то выполняется действие (или набор действий), идущее по ветви ЛОЖЬ для каждого из условий. На рис. 6.6 представлена блок-схема команды «Выбор» для п = 3.
6.3.3. Алгоритмическое конструкция «Цикл»
Циклической (или циклом) называют алгоритмическую конструкцию, в которой некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на
каждом шагу цикла называет-
| Правило изменения параметра i: i = N, К, h означает | |
| 1-й шаг цикла | |
| 2-й шаг цикла | / = N + h |
| 3-й шаг цикла и т.д. | / - N + 2h |
| последний шаг |
ся телом цикла. Любая циклическая конструкция содержит в себе элементы ветвящейся алгоритмической конструкции.
Рассмотрим три типа циклических алгоритмов: цикл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их называют итерационными).
Арифметический цикл
В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (И) его изменения. Те., на первом шаге цикла значение параметра равно N, на втором - N + h, на третьем - N + 2п и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К.
Пример 6.4.
Вывести 10 раз слово «Привет!».
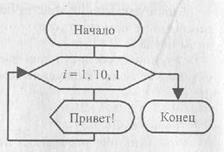
Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При / = 1 будет выведено первое слово, при / = 2 будет выведено второе слова и т.д. Так как требуется вывести 10 слов, то последнее значение параметра / = 10. В заданном примере требуется 10 раз повторить одно и то же действие: вывести слово «Привет!». Составим алгоритм, используя арифметический цикл, в котором правило изменения параметра / — 1, 10, 1. Т.е. начальное значение параметра / — 1; конечное значение i = 10; шаг изменения h = 1. На рис. 6.7 представлена блок-схема алгоритма решения данной задачи.
|
Рис. 6.7. Блок-схема к примеру 6.4
Цикл с предусловием
|
| б |
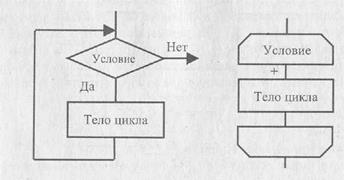
Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ЛОЖЬ. При первом же несоблюдении условия цикл завершается.
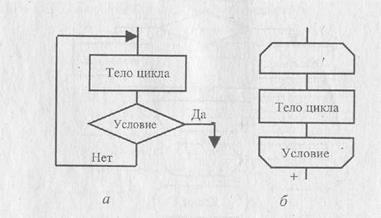
Блок-схема данной конструкции представлена на рис. 6.8 двумя способами: с помощью условного блока а и с помощью блока границы цикла б.
Особенностью цикла с предусловием является то, что если изначально условное выражение ложно, то тело цикла не выполнится ни разу.
Пример 6.5.
Одним из наиболее распространенных алгоритмов, встречающихся в литературе по информатике, является алгоритм Евклида — алгоритм нахождения наибольшего общего делителя двух натуральных чисел т и п (рис.6.9).
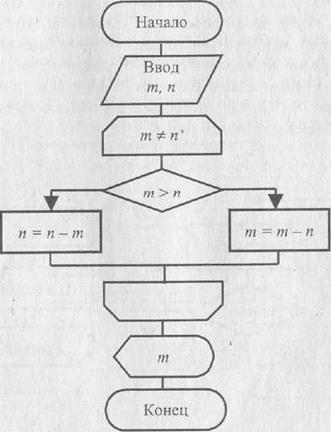
Рис. 6.8. Блок-схема цикла с предусловием
Опишем его на псевдокоде:
1. Ввод натуральных чисел тип.
2. Пока 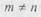 делать.
делать.
2.1. Если т>п, то т=т — п,
иначе п =п — т.
2.2. Переход к шагу 2.
. 3. Вывод т (найденный наибольший общий делитель). 4. Конец.
Цикл с постусловием
| Рис. 6.10. Блок-схема цикла с постусловием |
Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается. Блок-схема данной конструкции представлена на рис. 6. L0 двумя способами: с помощью условного блока а и с помощью блока управления 6.
Пример 6.6.
Составим алгоритм игры «Угадай число». Первый игрок вводит задуманное число от 1 до 50. Второй (угадывающий) вводит другое число и получает один из ответов: «Ваше число меньше», «Ваше число больше» или «Вы угадали». Игра продолжается до тех пор, пока второй игрок не угадает задуманное число.
Составляя алгоритм игры, обозначим х — число, задуманное первым игроком, у — число, вводимое на очередном шаге вторым игроком. Блок-схема алгоритма приведена на рис. 6.11.
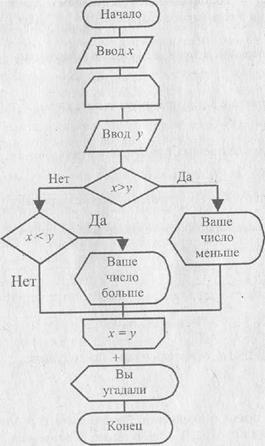
Рис. 6.11. Блок-схема игры «Угадай число» (пример 6.6)
Рассмотрим стандартные циклические алгоритмы, такие как вычисление суммы и подсчет количества элементов, удовлетворяющих некоторому признаку.
Суммирование.
Пример 6.7.
Для заданного натурального числа N вычислить сумму
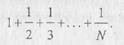
Подсчет суммы осуществляется следующим образом. Сначала считаем, что сумма S есть первое слагаемое (S = 1). Далее к первому сла-
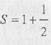
|
| ■ Но |
гаемому прибавляем второе, получаем новую сумму
на предыдущем шаге S = 1, поэтому можно записать  К сумме двух первых слагаемых прибавляем третье
К сумме двух первых слагаемых прибавляем третье  . Но на
. Но на
предыдущем шагу 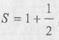 , поэтому можно записать
, поэтому можно записать 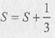 и т.д.
и т.д.
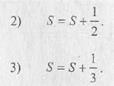
|
| Запишем i-й шаг, опираясь на два предыдущих: |
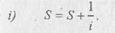
|
Получили следующую последовательность шагов: I) S = 1.
Выясним правило изменения номера шага i. В описанной последовательности г = 1, 2, 3 и т.д. В сумме N слагаемых, поэтому последним значением i будет N. Отсюда нашли правило изменения i = 1, N, 1.
Сверяя инструкции каждого шага, находим, что выражение на первом шаге отличается от других (однотипных). Чтобы оно стало таким как все, в сумму надо добавить S, т.е. записать: S = S + 1 (учитываем, что 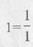 ). Отсюда для S возникает необходимость задания
). Отсюда для S возникает необходимость задания
начального значения, но такого, чтобы S + 1 = 1 (таким должно быть выражение для / — 1), этим числом является нуль, при сложении с нулем сумма не меняется.
Так как известно число шагов цикла, то для построения алгоритма используем цикл с параметром /.
Алгоритм на псевдокоде:
1. Ввод N.
2. S = 0.
3. Для i = 1, N, 1 повторить:
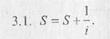
4. Вывод S.
5. Конец.
Блок-схема алгоритма приведена на рис. 6.12.


 Сформулируем правило суммирования:
Сформулируем правило суммирования:
• начальное значение суммы S = 0;
• в теле некоторой циклической конструкции
выполнить команду:
S = S + <слагаемое>.

 Упражнения для самостоятельной работы:
Упражнения для самостоятельной работы:
Для заданного натурального числа N вычислите суммы N-сла-гаемых:

 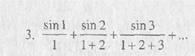
|
Рис. 6.12. Алгоритм вычисления суммы
^Подсчет количества элементов. Произведем счет: 1, 2, 3, 4, 5 и т.д., этот процесс является циклическим, так как каждый раз мы совершаем одно и то же действие: предыдущее натуральное число увеличиваем на единицу. Обозначив через К — счетчик искомых элементов, легко получить правило счетчика: К = К + 1 (на очередном шаге цикла). Но при первом подсчете должны получить значение К, равное единице, а до начала счета счетчик должен быть пуст, следовательно, начальное значение счетчика равно нулю.

 Правило счетчика:
Правило счетчика:
• начальное значение счетчика К = 0;
• в.теле некоторой циклической конструкции
выполнить команду:
К = К+ 1.
Пример 6.8
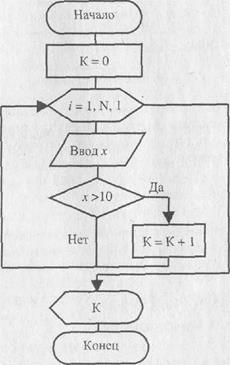
Задано 20 чисел. Сколько среди них чисел, больших 10? Псевдокод:
1. К = 0 {Счетчик чисел, больших 10}.
2. Повторить 20 раз (для / = 1, 20, 1).
2.1. Ввод числа х.
2.2. Если х > 10, то К = К+ 1.
3. Вывод К.
4. Конец.
| Рис. 6.13. Алгоритм примера 6.8 |
Блок-схема алгоритма приведена на рис. 6.13. Замечание: в фигурных скобках {....} принято помещать комментарии к алгоритму.
В каждом из рассмотренных выше примеров использовалась одна циклическая конструкция. В реальных задачах может встретиться любое число циклов. Обозначив цикл квадратной скобкой, схематично представим варианты взаимного расположения циклов (рис. 6.14).
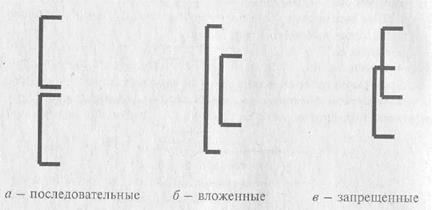 Рис. 6.14. Расположение циклов
Рис. 6.14. Расположение циклов
Алгоритм любой задачи может быть представлен как комбинация представленных выше элементарных алгоритмических структур, поэтому данные конструкции: линейную, ветвящуюся и циклическую, называют базовыми.
6.3,4. Рекурсивный алгоритм
Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.
6,4. Простые типы данных: переменные и константы
Реальные данные, которые обрабатывает программа, — это целые и. вещественные числа, символы и логические величины. Эти простые типы данных называют базовыми. Все данные, обрабатываемые компьютером, хранятся в ячейках памяти компьютера, каждая из которых имеет свой адрес. Для того чтобы не следить за тем, по какому адресу будут записаны те или иные данные, в языках программирования используется понятие переменной, позволяющее отвлечься от адреса ячейки памяти и обращаться к ней с помощью имени (идентификатора).
Переменная — есть именованный объект (ячейка памяти), который может изменять свое значение. Имя переменной указывает на значение, а способ ее хранения и адрес остаются скрытыми от программиста. Кроме имени и значения, переменная имеет тип, определяющий, какая информация находится в памяти. Тип переменной
задает:
• используемый способ записи информации в ячейки памяти;
• необходимый объем памяти для ее хранения.
Объем памяти для каждого типа определяется таким образом, чтобы в него можно было поместить любое значение из допустимого диапазона значений данного типа. Например, тип «байт» может принимать значения от 0 до 255, что в двоичном коде (255 10) = = 11111111 2) соответствует ячейке памяти длиной в 8 бит (или 1 байт).
В описанных выше алгоритмах (примеры 6.1 - 6.8) все данные хранятся в виде переменных. Например, инструкция «Ввод двух чисел а, Ь» означает введение пользователем значений двух переменных, а инструкция «К=К+1» означает увеличение значения переменной К на единицу.
Если переменные присутствуют в программе, на протяжении всего времени ее работы — их называют статическими. Переменные, создающиеся и уничтожающиеся на разных этапах выполнения программы, называют динамическими.
Все остальные данные в программе, значения которых не изменяются на протяжении ее работы, называют константами или постоянными. Константы, как и переменные, имеют тип. Их можно указывать явно, например, в инструкции «К = К + 1» 1 есть константа, или для удобства обозначать идентификаторами: pi = 3,1415926536. Только значение pi нельзя изменить, так как это константа, а не переменная.






