Задачі на знаходження четвертого пропорційного містять три пропорційні величини, одна з яких є однаковою для обох випадків. В третьому класі учні навчилися розв’язувати такі задачі способом наведення до одиниці. До ускладнених задач на знаходження четвертого пропорційного відносяться задачі на подвійне наведення до одиниці.
Підготовча робота.
Задача 1. На 3 дня 6 вівцям дають 36 кг сіна. Скільки сіна дають на 1 день 6 вівцям?
- Про що розповідається в задачі? (Про вівці.) Скільки тварин приймає участь в задачі? (6). І в умові задачі йде мова про 6 тварин і запитується про 6 тварин. Отже цю задачу коротко можна записати так:
|
- За коротким записом поясніть числа задачі. (Число 3 означає час, який годували 6 тварин сіном. Число 36 означає загальну масу сіна, яку дали 6 тваринам за цей час.)
- Яке запитання задачі? (Скільки сіна дадуть 6 вівцям за 1 день?)
- Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: 1 – загальну масу сіна для 6 тварин, відомо 36 кг, та П – час, який годували 6 тварин, відомо 3 дні.)
- Якою арифметичною дією відповімо на запитання задачі? (Дією ділення. Щоб знайти масу сіна на 1 день, треба загальну масу сіна поділити на час.)
-  Чи можна відразу відповісти на запитання задачі? (Так, тому що відомі обидва числові значення.)
Чи можна відразу відповісти на запитання задачі? (Так, тому що відомі обидва числові значення.)
?
 |  |


36: 3
- Запишіть розв’язання задачі. (36: 3 = 12 (кг))
- Запишіть відповідь. (Відповідь: 12 кг сіна треба 6 вівцям на 1 день.)
- Як ми відповіли на запитання задачі? (Ми загальну масу поділили на час.) Покажемо це дужкою на короткому записі:
 |
|
Далі вчитель продовжує ситуацію задачі:
Задача 2. Шести вівцям на 1 день дають 12 кг сіна. Скільки сіна дають 1 вівці на 1 день?
Це не складна задача, і учні її розв’язують усно. На дошці записується короткий запис, схема аналізу і розв’язання:
 |

?
 |  |


12: 6
Розв’язання:
12: 6 = 2 (кг)
Відповідь: 2 кг сіна треба 1 вівці на 1 день.
Ознайомлення.
Ознайомлення з новим видом задач здійснюється на підставі задачі, яка є поєднанням двох попередніх задач:
Задача. На 3 дні 6 вівцям дають 36 кг сіна. Скільки сіна дають 1 вівці на день?
- Запишімо цю задачу коротко.
|
- Порівняйте цю задачу з першою задачею. Що в них спільного? (Умова.) Чим вони відрізняються? (Запитаннями)
- Порівняйте цю задачу з другою задачею. Що в них спільного? (Запитання.) Чим вони відрізняються? (Умовами.)
- Що цікавого ви помітили? (Ця задача складається з двох попередніх задач.)
- За коротким записом поясніть числа задачі. (Число 3 означає час, який годували тварин. Число 6 означає кількість тварин. Число 36 означає загальну масу тварин.)
- Повторіть запитання задачі.
- Що треба знати, щоб відповісти на запитання задачі “Скільки сіна дають 1 вівці на день?” (Треба знати два числові значення: 1 – масу сіна на 1 день, що дають усім вівцям (не відомо), та П – кількість тварин (відомо, 6).)
- Якою арифметичною дією відповімо на запитання задачі? (Дією ділення.)
- Чи можна відразу відповісти на запитання задачі? (Не можна, ми не знаємо масу сіна на 1 день для шести тварин.)
- Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – загальну масу сіна, відомо 36 кг), та П – час, який годували усіх тварин.)
- Якою арифметичною дією відповімо на запитання? (Дією ділення)
 ?
?
 |  |


2)?: 6
 |  |


1) 36: 3
- Складіть план розв’язування задачі. (Першою дією ми дізнаємося про масу сіна на 1 день для 6 вівців. Другою дією ми дізнаємося про масу сіна на 1 день для 1 вівці.)
-  Запишіть розв’язання задачі.
Запишіть розв’язання задачі.
 :
:
1) 36: 3 = 12 (кг) на 1 день 6 вівцям.
2) 12: 6 = 2 (кг) на 1 день 1 вівці.
- Запишіть відповідь. (Відповідь: 2 кг сіна дають 1 вівці на день.)
- Про що ми дізналися першою дією? (Про масу сіна на 1 день для однієї вівці.) Покажемо це стрілочкою на короткому записі:
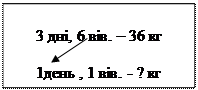 |
- Як ми про це дізналися? (Ми загальну масу поділили на час.) Покажемо це дужкою на короткому записі:
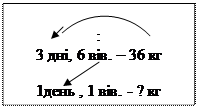 |
- Уважно розгляньте інше розв’язання:
1) 36: 6 = 6 (кг)
2) 6: 3 = 2 (кг)
- Поясніть про що дізнаємося кожною дією. (В першій дії поділили загальну масу сіна на кількість вівців, тому отримали масу сіна для 1 вівці на 3 дні.) Це можна показати стрілочкою і дужкою на короткому записі:
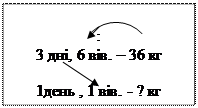 |
- Про що дізналися другою дією? (Другою дією відповіли на запитання задачі і знайшли масу сіна для 1 вівці на 1 день.)
- Чим цікава ця задача? (Вона розв’язується двома способами.) Чим відрізняються ці способи? (Першою дією. В першому способі ми дізналися про масу сіна на 1 день для 6 вівців. А в другому – про масу сіна на 3 дні для 1 вівці.) Що в них спільного? (Другою дією відповіли на запитання задачі – знайшли масу сіна для 1 вівці на 1 день.)
- Що ж ще спільного є в цих способах міркування? В першій дії ми знайшли величину однієї одиниці (чи на 1 день для 6 вівців; чи на 3 дні для 1 вівці. В другій дії ми також знайшли величину однієї одиниці – на 1 день для 1 вівці. Таким чином, в цій задачі ми двічі наводили до одиниці.
На етапі закріплення, учням пропонується кілька задач даного виду; діти спочатку складають короткий запис задачі, потім порівнюють його з опорною (вище розглянутою) задачею і роблять висновок, що дана задача такого ж самого виду – на подвійне наведення до одиниці, вона розв’язується двома способами (ставлять стрілочки і дужки) і розповідають план розв’язування за кожним з них. Наприклад:
 |
1 спосіб. Першою дією дізнаємося масу силосу для 6 корів на 1 день. Другою дією дізнаємося про масу силосу для 1 корови на 1 день.
2 спосіб. Першою дією дізнаємося про масу силосу для 1 корови на 4 дні. Другою дією дізнаємося про масу силосу для 1 корови на 1 день.
Ознайомлення учнів з задачами на подвійне зведення до одиниці П виду.
Задача 1. (1 вид) В зоопарку за 3 дні 5 моржам дали 30 кг риби. Скільки кілограмів риби треба 1 моржу на 1 день?
Це задача відомого виду, учні впізнають її і розв’язують самостійно:
 | |||
 |
|
1 спосіб. Першою дією дізнаємося масу риби для 5 моржів на 1 день. Другою дією дізнаємося про масу риби для 1 моржа на 1 день.
 2 спосіб. Першою дією дізнаємося про масу риби для 1 моржа на 3 дні. Другою дією дізнаємося про масу риби для 1 моржа на 1 день.
2 спосіб. Першою дією дізнаємося про масу риби для 1 моржа на 3 дні. Другою дією дізнаємося про масу риби для 1 моржа на 1 день.
Розв’язання:
 1 спосіб::
1 спосіб::
1) 30: 3 = 10 (кг) риби 5 моржам на 1 день.
2) 10: 5 = 2 (кг) риби 1 можу на 1 день.
 |
 П спосіб::
П спосіб::
1) 30: 5 = 6 (кг) риби 1 можу на 3 дні.
2) 6: 3 = 2 (кг) риби 1 моржу на 1 день.
Відповідь: 2 кг риби 1 моржу на 1 день.
Далі учням пропонується скласти обернену задачу, в якій запитувалось про масу риби для 5 моржів на 3 дні.
Задача 2. (П вид). На 1 день 1 можу дають 2 кг риби. Скільки кілограмів риби дадуть 5 моржам за 3 дні?
Записуємо задачу коротко, зазначаючи, що число днів пишімо одно під одним, число моржів пишімо одно під одним.
|
- За коротким записом поясніть числа задачі. Повторіть запитання задачі.
- Порівняйте цю задачу з попередньою. Що цікавого ви помітили? (Короткі записи однієї структури.) Отже ця задача також розв’язується двома способами. Поставте стрілочку і розкажіть план розв’язування за 1 способом:
 |
|
 |
Другий спосіб. Першою дією дізнаємося, скільки кілограмів риби потрібно на 1 день 5 моржам. Другою дією відповімо на запитання задачі, і дізнаємося про масу риби на 3 дні для 5 моржів.
Розв’язання:
1 спосіб.
1) 2 * 3 = 6 (кг) риби для 1 моржа на 3 дні
2) 6 * 5 = 30 (кг) риби для 5 моржів на 3 дні.
П спосіб.
1) 2 * 5 = 10 (кг) риби на 1 день для 5 моржів.
2) 10 * 3 = 30 (кг) риби на 3 дні для 5 моржів.
- Порівняйте розв’язки цих задач. Чим вони відрізняються? (Перша задача розв’язується двома діями ділення, а друга задача – двома діями множення.)
- Ви сказали, що ці задачі мають схожі короткі записи, тому вони відносяться до одного виду. Але перша задача розв’язується двома арифметичними діями ділення, а друга – двома арифметичними діями множення. Тому, щоб розрізнити такі задачі, говорять, що перша задача – це задача першого виду, а друга задача – це задача другого виду.
На етапі закріплення прочитавши задачі діти складають їх короткий запис, визначають вид задачі; роблять висновок про два способи розв’язання; ставлять стрілочки і розв’язують задачі двома способами. Після розв’язання по діях з поясненням, записують розв’язок виразом.
Що стосується роботи над задачею після її розв’язання, то учні складають обернені задачі: задачу 1 виду перетворюють в задачу П виду і навпаки.
Задачі на спільну роботу.
Підготовча робота.
М.О.Бантова радить на ступені підготовчої роботи розв’язати таку задачу: “ Батько може скопати рядок за 30 хвилин, а син – за 40 хвилин. Якщо вони працюватимуть разом, для того щоб скопати цей рядок, їм потрібно більше чи менше часу, ніж 30 хвилин? Ніж 40 хвилин?”
Учні міркують приблизно так: “ Потрібно часу менше, ніж 30 хвилин, тому що батькові допомагає син.”
Автор радить і при розборі задачі на спільну роботу ставити запитання “Більше чи менше....?”. Відповідь на це запитання попередить можливі помилки у розв’язанні задач на спільну роботу, коли у відповіді отримаємо більше часу, ніж час роботи кожного.
Виходячи з цього на ступені підготовчої роботи пропонуємо задачу: “ Одна друкарка за годину друкує 5 сторінок, а інша – 4. Скільки сторінок надрукують за годину обидві друкарки?”
- Більше чи менше, ніж 5 надрукують за 1 годину обидві друкарки? (Більше, тому, що першій допомагатиме друга.)
- Що треба знати, щоб дізнатися, скільки сторінок надрукують разом обидві друкарки за 1 годину? (Треба знати два числові значення: 1 – скільки сторінок друкує перша друкарка – 5, та скільки сторінок друкує друга друкарка – 4.)
- Якою арифметичною дією відповімо на запитання задачі? (Дією додавання.)
- Запишіть розв’язання. (5 + 4 = 9 (с.))
- Відповідайте на запитання задачі. (Відповідь: 9 сторінок надрукують друкарки, якщо працюватимуть разом.)
Ознайомлення.
Задача. Одна друкарка друкує за годину 5 сторінок, інша 4. Скільки годин вони повинні працювати разом, щоб надрукувати 72 сторінки?”.
Розглянемо методику роботи над цією задачею:
- Про що розповідається в задачі? (Про друкарок.)
- Розгляньте короткий запис задачі.
| Кількість сторінок за 1 год. | Загальна кількість сторінок | Час роботи | |
| 5 с. | 
| 
| |
| 72 с. | ? | ||
| П | 4 с. |
- За коротким записом поясніть, що означають числа задачі.
- Назвіть запитання задачі.
- Обидві друкарки надрукують 72 сторінки швидше чи повільніше, ніж перша друкарка? Ніж друга друкарка? (Швидше, тому що за годину вони друкуватимуть більше сторінок, якщо працюватимуть разом.)
- За одну годину вони разом надрукують більше чи менше сторінок, ніж 5? Ніж 4? (Вони разом за 1 годину надрукують більше сторінок, тому що одній допомагатиме інша.)
- Повторіть запитання задачі. Що треба знати, щоб на нього відповісти? (Треба знати два числові значення: 1 – загальну кількість сторінок, 72, та П – кількість сторінок, що друкують обидві друкарки за 1 годину, не відомо.)
- Якою дією відповімо на запитання задачі? (Дією ділення.)
- Чи можна відразу відповісти на запитання задачі? (Ні, тому що ми не знаємо скільки сторінок, що друкують обидві друкарки за 1 годину.)
- Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – кількість сторінок, що друкує перша друкарка за 1 годину, 5, та П – кількість сторінок, що друкує друга друкарка за годину, 4.)
- Якою арифметичною дією відповімо на запитання? (Дією додавання.)
- Чи можна відразу відповісти на це запитання? (Та. Аналіз закінчено.)
 ?
?
 |


72:?
 |


5 + 4
- Складіть план розв’язування задачі.
- Запишіть розв’язання по діях з поясненням.
1) 5 + 4 = 9 (с.) друкують обидві друкарки разом за 1 годину.
2) 72: 9 = 8 – стільки годин потрібно обом друкаркам, щоб надрукувати 72 сторінки.
Або 72: (5+4) = 8
- Запишіть відповідь. (Відповідь: 8 годин друкарки повинні працювати разом, щоб надрукувати 72 сторінки.)
- Порівняйте цю задачу з попередньою. Що цікавого ви помітили? (Ця задача є продовженням попередньої.) Що в них спільного? (Спільне в умові кількість сторінок, що друкує кожна друкарка за 1 годину) Що в них відмітного? (У другій задачі в умові ще говориться про загальну кількість сторінок, що вони повинні надрукувати разом. Та в цих задачах інші запитання.)
- Що спільного в розв’язаннях? Чим відмічаються розв’язання?
- Про що ми дізналися в другій задачі? Ми дізналися про час їх спільної праці. Це задача на спільну роботу.
- Щоб впізнати задачу на спільну роботу, на які слова треба орієнтуватися? (“Працюючи разом.”)
- Змініть величини задачі. Складіть нову задачу.
- Чи це задача на спільну роботу?
- Чи треба її розв’язувати? (В нас вже є розв’язок цієї задачі, треба змінити лише пояснення.)
- Змініть числові дані. Розкажіть задачу.(Вчитель слідкує, щоб число, яке означає загальну величину ділилося на суму двох чисел, які означають одиницю цієї величини.)
- Чи схожа ця задача на попередню? До якого виду її можна віднести?
- Якщо всі ці задачі відносяться до задач на спільну роботу, то вони мабуть й мають однаковий план розв’язування?
- Розкажіть план розв’язання цієї задачі.
- Як впізнати задачу на спільну роботу? За яким планом вони розв’язуються?
5, 4, 72, 8. – пряма задача.
5, 4, 72, 8. – перша обернена задача.
Одна друкарка друкує за годину 5 сторінок, а інша 4 сторінки. Скільки сторінок вони надрукують за 8 год, якщо працюватимуть разом?
Розв’язання.
1 спосіб
1) 5 + 4 = 9 (с.) за 1 год друкують обидві друкарки, працюючи разом;
2) 9 * 8 = 72 (с.) за 8 год надрукують обидві друкарки, працюючи разом.
Або (5 + 4) * 8 = 72 (с.)
Треба зазначити, що за математичною структурою цю задачу можна віднести і до задач на знаходження суми двох добутків, тому вона розв’язується іншим способом:
1) 5 * 8 = 40 (с.) надрукує 1 друкарка за 8 год;
2) 4 * 8 = 32 (с.) надрукує 2 друкарка за 8 год;
3) 40 + 32 = 72 (с.) – надрукують обидві друкарки за 8 год.
Або 5 * 8 + 4 * 8 = 72 (с.)
Відповідь: 72 сторінки надрукують обидві друкарки за 8 год, працюючи разом.
Дві друкарки, працюючи разом за 8 год надрукували 72 сторінки. Скільки сторінок за 1 год друкує перша друкарка, якщо інша за 1 год друкує 4 сторінки?
Розв’язання.
1) 72: 8 = 9 (с.) за 1 год друкують обидві друкарки, працюючи разом;
2) 9 – 4 = 5 (с.) за 1 год друкує перша друкарка.
Або 72: 8 - 4 = 5 (с.)
Відповідь: 5 сторінок друкує за 1 годину перша друкарка.
Задача. “ Тесляр виготовляє за день 12 рам, а його помічник 7. Скільки рам вони зроблять разом за робочий тиждень (5 днів)? ”
Це задача іншої математичної структури (відносно даної прямої задачі), але її запитання містить слова “зробили разом за...”, тому її можна розглядати, як задачу на спільну роботу, тоді як в методичній літературі вона визначається, як задача на знаходження суми двох добутків. Отже її можна розв’язати й іншим способом:
1 спосіб:
1) 12 * 5 = 60 (шт..) рам виготовить тесляр за 5 днів.
2) 7 * 5 = 35 (шт..) рам виготовить помічник за 5 днів
3) 60 + 35 = 95 (шт.) рам виготовлять тесляр і помічник, працюючи разом за 5 днів.
Або 12 * 5 + 7 * 5 = 95 (шт..)
П спосіб:
1) 12 + 7 = 19 (шт..) рам виготовлять за день і тесляр і помічник, працюючи разом.
2) 19 * 5 = 95 (шт..) рам виготовлять за 5 днів і тесляр і помічник, працюючи разом.
Або (12 + 7) * 5 = 95 (шт..)
Відповідь: 95 рам виготовлять тесляр і помічник разом за робочий тиждень.
Для того, щоб впізнати задачу на спільну роботу треба вміти переформульовувати запитання задачі. Наприклад: “Скільки відер води дадуть обидва насоси за хвилину?”, це запитання можна пере формулювати так: “ Скільки відер води дадуть обидва насоси за хвилину, працюючи разом?”






