Обнаруживающие свойства циклического кода определяются видом полинома, задающего код, а именно, его степенью, числом членов, значностью кодовой комбинации. Имеется ряд теорем, которые позволяют судить об обнаруживающих способностях кода. Сформулируем и докажем их.
Теорема 1. Циклический код, образованный любым полиномом g(x), содержащим более одного члена, обнаруживает все одиночные ошибки.
Вектор одиночной ошибки е(х) имеет вид е(х)=хi, где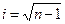 
. Очевидно, что хi не делится без остатка на многочлен, который состоит из более одного члена. Следовательно, теорема доказана.
Теорема 2. Любой кодовый многочлен циклического кода с порождающим многочленом g(x)=1+x содержит четное число членов.
Пусть v(x)=(1+x)*a(x) и информационный полином a(x) содержит «m» членов. После умножения будет два многочлена а(х) и х*а(х) каждый их которых также будет содержать по «m» членов. Из общего числа 2m членов часть может попарно уничтожится. Пусть таких пар m1. Остается членов 2m-2m1=2(m-m1) – четное число. Следствием этого является факт,
а) что g(x)=1+x обнаруживает все нечетные ошибки. Полином ошибок с нечетным числом единиц не является кодовым по теореме.
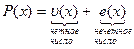, следовательно Р(х) содержит нечетное число единиц запрещенных комбинаций.
б) Любой циклический код, образованный полиномом 1+х также обнаруживает все нечетные ошибки, такие как
1+х=(1+х)(1+х+х2+…+хl-1).
Определим понятие «пачка ошибок». Это группа символов, начинающаяся ошибкой и заканчивающаяся также ошибкой, между этими крайними ошибочными символами могут быть как правильные, так и ошибочные символы. В виде многочлена «пачка ошибок» записывается как
е(х)=хi+…+хj, i<j£n-1.
Длиной пачки называют число b=j-i+1, то есть это число символов в пачке, Очевидно, что b£n.
Теорема 3. Любой циклический код, образованный при помощи полинома степени (n-k), обнаруживает любую пачку ошибок длиной b=n-k и менее. Пачке ошибок длиной b=n-k соответствует полином
e(x)=xi+xi+1+…+xj=xi(xn-k-1+…+1).
Первый множитель xi не делится на образующий полином g(x), состоящий более, чем из одного члена. Второй множитель имеет степень n-k-1 или меньше. Степень полинома g(x)=(n-k) больше степени многочлена делимого. Следовательно, деление t(x) на g(x) без остатка невозможно, то есть пачка ошибок обнаруживается всегда.
Теорема 4. Относительная доля пачек ошибок длиной b=n-k+1, обнаруживае-мых циклическим (n,k) кодом равна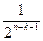 
(по отношению ко всем возможным пачкам длины n-k+1).
Вектор ошибки в этом случае будет иметь вид: e(x)=xi×e1(x), гду е1(х) обязательно содержит члены нулевой степени и степени n-k. Члены со степенями 1,2,… и n-k-1 могут либо присутствовать, либо их нет. Число таких наборов равно 2n-k-1.
Если ошибка e1(x) не обнаруживается, то e1(x)=g(x)×q(x), где e1(x) делится на образующий полином без остатка. Т.к. степень g(x) равна n-k, то степень q(x) равна n-k-n+k=0. Значит q(x)º1, то есть имеется ровно один вектор е1(х), который делится без остатка (он имеет вид образующего полинома). Получаем, что из 2n-k-1 различных пачек длиной n-k-1, не обнаруживается только одна, а относительное число необнаруживаемых пачек ошибок равно .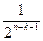
Теорема 5. Относительная часть пачек ошибок длиной b>n-k+1, необнаруживае-мых циклическим кодом (n,k), составляет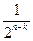 
от общего числа всех возможных пачек ошибок длиной b.
Для необнаруживаемых ошибок вектор ошибки e1(x)=g(x)×q(x). Если b>n-k+1, то полином q(x) имеет члены от x0 до xb-n+k-1, число слагаемых между этими крайними степенями, которые могут быть, а могут и не быть b-n+k-2, то есть имеется различных результатов от деления на g(x) – 2b-n+k-2 (необнаруживаемых пачек ошибок).
Число различных вариантов пачек ошибок длиной b будет равно 2b-2. Следовательно, часть необнаруживаемых пачек ошибок составляет 
, что и следовало доказать.
