Под декодированием обычно подразумевают процедуры исправления ошибок. Алгоритмов исправления много. Это обусловлено тем, что не всегда пытаются реализовать весь потенциал кода по исправлению ошибок и за счет этого сложность технической реализации весьма существенно снижается.
Декодер может быть полным, т.е. всегда выносить решение, или неполным, когда возможно стирание блоков, ошибки в которых не могут быть исправлены. Риск ошибиться у полного декодера гораздо больше.
Наиболее общим способом декодирования, реализующим всю корректирующую способность кода, является декодирование по максимуму правдоподобия (минимуму расстояния). Суть его – сравнение принятого из канала слова с каждым из возможных кодовых слов и вынесения решения в пользу того кодового слова, к которому ближе всего канальное слово. Сложность такого декодера велика, растет по экспоненте в зависимости от числа информационных символов. По этой причине, в чистом виде декодер такого типа для длинных кодов нереализуем, но за счет использования дополнительной информации о ненадежных символах блока, пространство поиска резко сужается. Такой декодер часто применяется.
Чтобы реализовать этот метод, целесообразно построить таблицу стандартной расстановки. Как эта таблица получается, проще всего пояснить на примере группового кода, код в этом случае есть подгруппа. Элементы подгруппы - кодовые комбинации. Их запишем в первую строку таблицы, поместив нулевую комбинацию в начало, и разложим группу по смежным классам. Все возможные на приеме последовательности будут содержаться в таблице.
| Лидеры смежных классов | 
| . | 
| 
| … | 
|
| . | 
| 
| … | 
| |
| . | 
| 
| … | 
| |
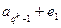
| Смежный класс | ||||||
| . | 
| 
| … | 
| |
| . | 
| 
| … | 
|
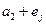
Каждая строка образует смежный класс. Первый элемент строки называют лидером смежного класса (образующим). Если в качестве лидеров выбраны элементы строки с минимальным весом, то приведенная таблица называется стандартной расстановкой. Весом смежного класса считают вес его лидера.
Пусть а - переданное слово; 
- принятая последовательность. Если используется ДСК без памяти, то в качестве лидеров надо выбирать векторы ошибок наиболее вероятные, т.е. с одиночной ошибкой, двойной и т.д., пока позволяют свойства кода. Декодирование будет состоять в следующем:
- находится в таблице последовательность, равная ;
- определяется лидер той строки, в которой оказалась последовательность ;
- вычисляется 
как результат декодирования.
Ценность стандартной расстановки относительна. Для больших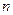 
и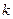 
технически реализовать такую таблицу на ЭВМ становится невозможным. Это не означает полного отрицания метода декодирования по максимуму правдоподобия. Обычно за счет дополнительной информации о достоверности символов удается ограничить "объем пространства" просматриваемых комбинаций. Типичным примером являются алгоритмы Чейза [13].
Синдромное декодирование
Синдромом вектора называет вектор 
, где 
- проверочная матрица. Если а - кодовый вектор, то, очевидно, 
. Утверждается, что все векторы, принадлежащие одному смежному классу, имеют совпадающие синдромы. Действительно, есл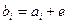и 
и 
- векторы одного смежного класса с образующим, равным 
, то 
, 
, т.е. 
.
Синдромы разных смежных классов различны. Декодирование будет состоять в вычислений синдрома ; нахождении в памяти лидера, соответствующего этому синдрому, выдачи результата декодирования в виде 
.
Кодирование проще выполнять систематическим кодом. В этом случае необходимо вычислить значения 
проверочных символов. Каждый проверочный символ согласно алгоритму кодирования (матричное умножение) есть сумма по модулю два самое большее 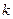информационных символов. Следовательно, число двоичных сумматоров в схеме кодера будет не больше 
. Для согласования скоростей приема безизбыточных данных от источника и передачи закодированного сообщения в канал может потребоваться входной и выходной буферы из 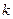и 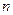ячеек памяти. Общая сложность 
, где 
- скорость кода.
Сложность декодера в первую очередь зависит от того, обнаруживаем мы ошибки или исправляем, является декодер полным или неполным. Декодирование по максимуму правдоподобия называют еще декодированием по манизму расстояния. Принятая комбинация сравнивается по метрике Хэмминга с каждой из кодовых и выбирается как решение та кодовая комбинация, к которой ближе всего принятая последовательность. Значит, потребуются 
- разрядных схем сравнения, буферные регистры и память для кодовых слов. Общая сложность составит 
, т.е. растет по экспоненте в зависимости от числа информационных разрядов. В неполном декодере предусматриваются сравнение полученного наименьшего расстояния со значением кодового расстояния, и отказ от декодирования, если это расстояние больше 
.
При синдромном декодировании на вычисление синдрома потребуется не более 
сумматоров и для полного декодера необходима память лидеров смежных классов (вариантов направляемых ошибок) на 
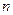-разрядных слов. Общая сложность будет составлять 
, т.е. сложность синдромного декодера растет по экспоненте в зависимости от числа избыточных символов. Если ошибки только обнаруживать, сложность декодера будет определяться схемой вычисления синдрома 
.
Относительно синдромного декодирования надо сделать два замечания. Во-первых, не обязательно в качества лидеров смежных классов надо брать векторы наименьшего веса. Вместо хэммингового расстояния в канале с пакетированием надо использовать комбинаторную метрику, т.е. исправлять наиболее вероятные варианты ошибок - пакеты. Во-вторых, не обязательно в памяти хранить все варианты ошибок, можно использовать математическую структуру кода (например, цикличность).
Мажоритарный декодер.
Основная идея, лежащая в основе алгоритма, заключается в том, что информационные символы могут быть вычислены через канальные символы разными способами. Решение выносится голосованием по большинству. Требуется, однако, выполнение некоторых условий к проверочным соотношениям. Это означает, что не любой код допускает мажоритарный вариант декодирования. Рассмотрим код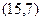 
с 
. Его проверочная матрица:
Проверочные соотношения, определяющие синдром, будут следующим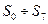и: 
или 
.
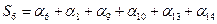
Поскольку, если нет ошибок, все 
, то и комбинации 
. Система проверок 
называется разделенной относительно последнего 
символа. Он входит во все проверочные соотношения, каждый другой символ только в одно. Если произошла одна ошибка в позиции 
, то получим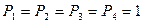 
. Если одна ошибка в любой другой позиции получим три единицы и ноль. Значит, ошибку в 14 позиции исправим по правилу: если 
, то 
, иначе 
.
Любая комбинация из двух ошибок, не содержащая , приведет к нарушению не более двух уравнений, а содержащая не менее трех. Значит можно по тому же правилу исправлять и все двойные ошибки. Рассматривается циклический код, поэтому ошибки в остальных позициях тоже исправляются по четырем соотношениям после циклического сдвига.
Рассмотренный код является кодом с одношаговым разделением. Более общий случай - 
-шаговое разделение. Основное достоинство алгоритма мажоритарного декодирования – простота. Если нужна высокая скорость и умеренный выигрыш от кодирования, то надо применять этот алгоритм. Ниже приведена схема декодера 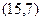- кода.
