Алгебраические основы теории кодирования

Группой называется множество вместе с бинарной операцией, заданной на этом множестве, обладающее следующими свойствами: замкнутости, ассоциативности, существование нейтрального элемента и наличие у каждого элемента обратного элемента. В кодировании представляют интерес конечные группы, т.е. порядок группы конечное число, а порядком называют число элементов в группе. Операцию в группе условно называют сложением или умножением. Если для выполняется условие , группа называется коммутативной (абелевой). Часть элементов группы с той же операцией могут тоже составлять группу. Последняя называется подгруппой. Группа разлагается по подгруппе на смежные классы. Производится это построением таблицы следующим образом. Первая строка таблицы это элементы подгруппы, на первое место помещается нейтральный элемент. Берется элемент группы , не содержащийся в первой строке, и получают вторую строку, выполняя операцию этого элемента с каждым из элементов подгруппы. Далее берется , не содержащийся в первых двух строках, и получают вторую строку и т.д., пока не исчерпаем все элементы .

Кольцо –это множество вместе с двумя бинарными операциями, называемыми сложение и умножение, при выполнении следующих свойств:

- образует абелеву группу по сложению,

- выполняется замкнутость по умножению и

- ассоциативность по умножению.

В кодировании интерес представляют коммутативные кольца с конечным числом элементов, в частности, кольца многочленов . «Аналогом» подгруппы в кольце будет идеал. Это подмножество элементов кольца, если выполняются условия:

,

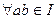, , и .

Особый интерес представляет поле. Полем называется множество с двумя операциями на нем (сложением и умножением), причем выполняются условия:

- группа по сложению,

- без нулевого элемента группа по умножению,

- выполняется дистрибутивный закон.

Конечные поля называются полями Галуа и обозначаются . Не из любого числа элементов можно настроить поле. Это возможно только когда - простое число или ;

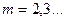
Чтобы задать (построить) поле надо привести таблицы сложения и умножения. Легко строится поле из простого числа элементов. Операции сложения и умножения определяются по модулю этого числа . Если - степень простого числа, поле строить труднее. Надо использовать неприводимый многочлен степени m с коэффициентами из простого подполя. Он играет роль простого числа, операции сложения и умножения определяются по модулю этого многочлена. Конечное поле заданного порядка единственно с точностью до обозначения элементов. Обозначение элементов, тем не менее, не безразлично. Так многочленное обозначение позволяет легко производить операцию сложения, а умножение весьма сложно. Его легче производить используя степенное представление элементов. Если взять какой-то элемент (ненулевой) поля и производить операцию умножения только над ним, то через определенное число шагов n произойдет циклическое повторение. Особый интерес представляют элементы, которые порождают все элементы поля. Они называются примитивными. Неприводимый многочлен, по модулю которого элемент х является примитивным, называется примитивным многочленом.

Построим поле , т.е. из 16 элементов. В качестве многочлена, по модулю которого будем строить таблицы умножения и сложения возьмем многочлен . Он неприводим над и является примитивным.

Представление элементов поля

Степенное	Многочлен	Двоичное	Десятичное

Множество называется линейным (векторным) пространством над полем , если для пар элементов из определена операция векторного сложения, а для элементов из и операция умножения вектора на скаляр, такие, что результат их выполнения дает элемент из , причем выполняются аксиомы:

- множество абелева группа по сложению;

- выполняется дистрибутивный закон для векторов, т.е. , ;

- выполняется дистрибутивный закон для скаляров, т.е. , ;

- выполняется ассоциативный закон, т.е. , .

Линейное пространство может быть задано базисными векторами. Это такие 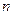линейно независимых векторов, которые позволяют любой вектор пространства выразить в виде . Минимально возможное число (п) линейно-независимых векторов есть размерность пространства.

Скалярным произведением векторов называется скаляр, определяемый по правилу . Если , то такие вектора ортогональны.

Множество всех векторов пространства , ортогональных пространству , образует подпространство , которое называют нулевым для .

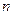Если некоторый вектор ортогонален базисным векторам , то он принадлежит . Если имеет размерность , подпространство размерность , то размерность равна .

Задание линейных кодов

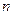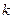Пусть - линейное -мерное пространство над полем . Линейным блоковым -м кодом размерности длины 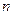называется всякое -мерное подпространство пространства . Для обозначения линейного кода используется символ -код.

Встречается другое название линейного кода (групповой код), которое связано с понятием группы. Двоичный код называют групповым, если сумма двух любых его кодовых слов есть снова кодовое слово. Это есть следствие из свойств группы.

Существует несколько способов задания линейных кодов. В зависимости от целей и задач оказывается удобным тот или иной способ представления.

1. Очевидно, что к линейно независимых векторов подпространства А, образующих его базис, позволяют выразить любой вектор этого пространства: ; , , - базисные векторы. Такой способ задания кода удобен для доказательства теорем, исследования свойств кода.

2. Если полученное соотношение записать в матричной форме

, , ,

где

то придем ко второй форме задания линейного кода. Матрица G, строки которой есть k линейно независимых векторов кода (например, базис­ные векторы, представленные через свои компоненты), называется порождающей матрицей -кода. Набор является информационным , . Набор 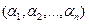- закодированное информационное сообщение.

Ясно, что для любого -кода А существует не одна порождающая матрица, так как всякая матрица QG, где Q - невырожденная матрица размером , тоже является порождающей матрицей -ко­да.

За счет перенумерации координат и выбора образующих векторов всегда можно порождающую матрицу привести к каноническому виду , где Е – единичная матрица размера , а В – произвольная матрица размера :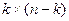

;

; ; ; .

Код, заданный канонической матрицей, является систематическим, т.е. проверочные и информационные символы разделены.

3. Задание кода с помощью проверочной матрицы .

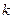Если задан код А как подпространство пространства размерности , то существует подпространство , ортогональное (называемое нулевым) размерности . Это подпространство дает тоже линейный код. Обозначим его . Он называется дуальным (двойст­венным) к А.

Обозначим через Н порождающую матрицу кода . Тогда код А можно определить как множество векторов таких, что

(*)

Матрица Н называется проверочной матрицей -кода. Если, как и раньше, обозначить компоненты вектора , элементы матрицы - , , , то развернутая запись матричного уравнения приведет к системе уравнений из штук вида .

Это означает, что компоненты любого кодового слова удовлетворяют со­вокупности линейных независимых однородных уравнений. Эти уравнения называется обобщенными проверками на четность. Для двоич­ного кода они представляет проверку на четность определенных групп информационных символов.

Так как уравнение (*) справедливо для всех слов кода, то оно справедливо и для строк порождающей матрицы (базисных векторов). Следовательно, проверочная и порождающая матрицы кода связаны соот­ношением .

Всякая проверочная матрица -кода комбинаторно эквивалентна матрице, представленной в канонической форме:

, , , .

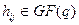Связь между проверочной и порождающей матрицей устанавливается следующей теоремой.

Пусть - порождающая матрица - кода, представленная в канонической форме, т.е. - единичная матрица разме­ра ; - матрица размера 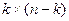с элементами из поля . Тогда матрица - проверочная матрица -ко­да , представленная в канонической форме.

Задание кода проверочной матрицей удобно для осуществления де­кодирования.

4. Модулярное представление кода. Производящая матрица кода G может иметь разнообразие типов столбцов в штук, так как в столбце 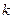символов и чисто нулевой столбец не имеет смысла. Если все типы столбцов записать в виде матрицы М размерности , то код можно задать, указав положительных чисел , где - число столбцов типа в матрице G:

.

Это и есть модулярное задание кода. дает в результате все ненулевые кодовые векторы. Важную роль играет матрица . Это симметричная матрица, содержащая по одному столбцу каждого типа.

Свойства линейных кодов

Так как расстояние между двумя векторами и равно весу суммарного вектора , а для линейного кода суммар­ный вектор тоже принадлежит коду, то кодовое расстояние равно минимальному весу множества кодовых векторов . Поскольку минимум берется по всем векторам кода А отличным от нулевого, то для поиска кодового расстояния достаточно сравнений. Для произвольного кода число сравнений равно . По виду матрицы Н можно судить о защитных свойствах кода, в частности, о значении кодового расстояния.

1. Теорема. Если любые столбцов матрицы линейно независимы, то кодовое расстояние не меньше, чем .

Доказательство. Пусть матрица Н обладает свойством, что столбцов линейно независимы, - кодовый вектор. Тогда или, раскрыв матричную запись, получим . Число элементов (т.е. столбцов Н), реально участвующих в проверках, очевидно, равно числу ненулевых компонент вектора , т.е. весу кодового вектора. В силу условия линейной не­зависимости столбцов матрицы Н равенство нулю возможно только при d или большем числе ненулевых ;. Значит, минимальный вес ко­дового вектора равен d или больше и кодовое расстояние тоже d или больше. Теорема доказана.

Можно, как следствие, заметить, что если все столбцы матрицы Н различны, то кодовое расстояние равно трем или больше. Действительно, при всех различных столбцах никакие два из них в сумме не равны нулю, т.е. линейно независимы. Отсюда .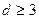

2. Если имеется модулярное представление кода, в частности дво­ичного, то спектр этого кода можно найти на основании теоремы Макдональда.

Веса каждого из ненулевых кодовых слов двоичного группового кода могут быть найдены как компоненты вектора, получающегося в результате матричного умножения (как матриц с действительными числами) вектора модулярного представления кода на матрицу : или . Веса кодовых слов оказываются упорядоченными так же, как кодовые слова в матрице .

3. Граница Синглтона. Минимальный вес любого линейного -кода удовлетворяет неравенству .

Доказательство. Ненулевое слово минимального веса имеет вес d. Имеются слова в систематическом коде о одним ненулевым информационным символом. Так как еще имеется только проверочных символов в слове, то вес не может быть больше 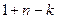. Код с называется кодом с максимальным расстоянием.

4. Спектры линейного кода А и двойственного ему взаимосвязаны. Эта связь оказалась весьма полезной для расчета спектров многих блоковых кодов. Пусть - спектральная функция -кода А, - спектральная функция . Согласно тождеству Мак-Вильямс:

(*)

Спектры кодов до в настоящее время находятся с помощью ЭВМ. С помощью (*) удается найти спектр кода большей длины, лишь бы число проверочных символов не превышало 32.