Первый способ задания циклического (n,k) кода уже был рассмотрен. Это задание кода образующим многочленом g(x). Отношение 
есть многочлен степени k. Он называется проверочным многочленом кода. Если знаем h(x), то (n,k)- код также задан.
Поскольку циклический код есть частный случай линейного кода, то он может быть задан порождающей матрицей кода или проверочной матрицей.
Зная g(x), найти k линейно независимых строк матрицы G весьма просто. Запишем в первую строку G коэффициенты:
g(x)=g0+g1x+g2x2+…+gn-kxn-k+0*xn-k+1+…+0*xn-1.
Вторая строка получается сдвигом на один символ вправо x*g(x) и так далее до (k-1) сдвига.
Приходим к несистематическому (n,k) -коду.
Аналогично, по проверочному многочлену строится проверочная матрица:
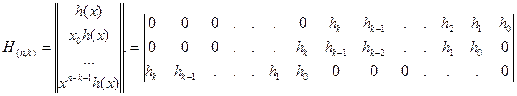
Чтобы найти каноническую форму порождающей матрицы, вычисляют остатки от деления xj+n-k-1 на g(x),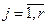 
и тогда 
, где Еk – единичная матрица, а j -ая строка в матрице R есть указанный выше остаток.
Многочлен h(x) записывается в матрице H справа, начиная со старшего коэффициента.
Циклический код может быть задан корнями образующего многочлена a1, a2 …,ar. Коды, задаваемые корнями, называют кодами БЧХ, по фамилиям авторов, предложивших такие коды (Боуз, Чаудхури, Хоквингем). Является ли некоторый набор (а1 а2 … аn-1) и соответствующий ему многочлен a(x)=an-1xn-1+ an-2xn-2+…+ a1x+a кодовым можно проверить, подставив вместо x значения корней. Если a(x= a I)=0, 
, то a(x) – кодовый многочлен.
Многообразие задания кодов связано с решением конкретных задач. Так кодер строиться по g(x) или h(x). Ошибки обнаруживаются по g(x) или по h(x). Матричное задание циклического кода может потребоваться для процедур исправления ошибок, например, мажоритарного декодирования. Задание кода корнями позволяет конструировать код с требуемыми свойствами.
Задача кодирования заключается в формировании по инфирмационным словам m(x) кодовых слов a(x) циклического (n,k)-кода, который по своей структуре может быть несистематическим и систематическим.
Формирование кодовых слов несистематического кода заключается в умножении многочлена m(x), отображающего информационную последовательность длины k, на порождающий многочлен, т.е. a(x)=m(x)g(x). Формирование кодовых слов систематического кода заключается в преобразовании информационной последовательности m(x) в соответствии с выражением a(x)=m(x) xr+r(x).
Проверочная последовательность r(x) определяется двумя способами:
при использовании «классического» способа кодирования 
;
при использовании способа кодирования, рекомендованного МККТТ 
, где x(1)r-1 – единичный многочлен степени (r-1).
Указанные выше матеметические операции выполняют кодеры несистематического и системетического кодов, которые могут быть реализованы наиболее просто аппаратным способом, но реализуются и програмно.
Процедура декодирования циклического кода с обнаружением ошибок, по аналогиис процессом кодирования, использует два способа:
- при кодировании «классическим» декодирование основано на использовании свойства делимости без остатка кодового многочлена а(х) циклического (n,k)-кода на порждающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом а(х) на g(x), вычисление и анализ остатка r(x). Если r(x)¹0, то принятое кодовое слово стирается и формируется сигнал «ошибка».
- при кодировании способом МККТТ декодирование основано на свойстве получения определенного контрольного остатка R0(x) при делении принятого кодового многочлена a(x) на порождающий многочлен. Поэтому, если полученный при делении остаток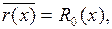 
то принятое кодовое слово считается неискаженным. Если остаток 
то принятое кодовое словое стирается и формируется сигнал «ошибка».
Значение контрольного остатка определяется из выражения 
