Пусть передан первый из сигналов, т.е.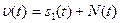 
.
Решение 
, в данном случае ошибочное, будет принято, если величина 
окажется больше величины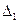 
.
или
.
Искомая вероятность ошибки равна:
где 
Величина 
имеет гауссовское распределение, т.к. 
- подчинено гауссовскому распределению и известно, что линейные преобразования гауссовских распределений есть тоже гауссовское распределение.
Найдем параметры распределения величины .
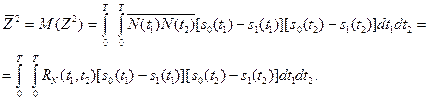
Поскольку шум белый, то 
.
Тогда:
Получаем, следовательно:
.
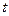Делаем замену переменной 
.
- функция нормального распределения табулирована.
Аналогично, можно показать, что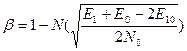 
и средняя вероятность ошибки:
.
Если вспомним определение расстояния между сигналами в Гильбертовском пространстве:
, то формулу для вероятности ошибки можно переписать в таком виде:
, где
- средняя энергия сигналов,
- мера несхожести сигналов (при 
совпадает с коэффициентом корреляции между сигналами).
Рассмотрим примеры.
1. Если бы сигналы были неразличимые, то 
,
- очевидный результат.
2. Пусть сигналы противоположны, т.е.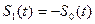 
. Этот случай соответствует двоичной фазовой модуляции со скачком фазы равным 
.
, 
3. Пусть сигналы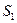 
и 
ортогональны. Этот случай соответствует частотной модуляции в частности.
,
4. Для случая амплитудной модуляции:
, 
, 
,
.
Как видно из формул, потенциальная помехоустойчивость определяется отношением энергии сигнала к спектральной мощности помех и видом (геометрией) сигналов. Максимальной помехоустойчивостью обладает система передачи с ФМ. Для получения одинаковой вероятности ошибки при использовании ортогональных сигналов требуется в два раза большая энергия, а при АМ в четыре раза большая, чем при ФМ.
График зависимости вероятности ошибки от отношения 
для ФМ, ЧМ и АМ сигналов приведен ниже. На рисунке показано, как выбирается разделяющая граница, и как изменяется в зависимости от вида сигналов расстояние между ними.
 
| ||||||||
| 10-1 | |||||||
| 10-2 | ||||||||
| 10-3 | ||||||||
| 10-4 | ||||||||
| 10-5 | ||||||||
| Ре |
Примеры помехоустойчивых систем сигналов
Бинарные противоположные сигналы
В этом случае 
- единственной колебание 
любой формы. Векторы сигналов 
и 
выбираются так, что 
и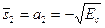 
.
Тогда 
.
Противоположными являются два сигнала любой формы, отличающиеся знаком.
Бинарные ортогональные сигналы
В этом случае 
, и 
- ортонормированные колебания. Векторы сигналов выбираются так:
.
Временные графики сигналов 
и 
зависят от вида ортонормального набора.
Так, если
.
М-ортогональные сигналы
В этом случае образуется М сигналов из 
- ортогональных колебаний 
с конфигурацией векторов:
.
Временные графики сигналов определяются набором ортонормальных колебаний. Например, можно взять
Тогда 
- сигналы являются отрезками гармонических колебаний кратных частот 
. Реализовывать технически такой набор не очень удобно.
Биортогональные сигналы
В этом случае из 
ортогональных колебаний образуется 
сигналов путем добавления к каждому из ортогональных сигналов противоположного сигнала.
Например, к векторам сигналов из п.2 
и 
добавляются 
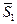- противоположный 
и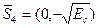 
- противоположный 
.
