В простейшем случае дискретный канал связи может быть представлен как симметричный канал без памяти (ДСК), т.е. такой стационарный дискретный канал, в котором вероятности искажения любого из символов 0 или 1 одинаковы. В этом канале вероятность передачи не зависит от статистики передаваемой последовательности. Воздействие помехи можно представить как позиционное суммирование входной последовательности символов, выдаваемых условным источником помехи, статистическая характеристика которой полностью определяет канал. В ДСК ошибки кратности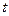 
подчиняются биномиальному закону распределения, поток ошибок задается через вероятность ошибки бита р. Вероятность 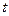-кратной ошибки на блоке из 
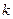символов равна:
Поток ошибок в ДСК без памяти является процессом восстановления с геометрическим распределением интервалов между ошибками 
.
Параметр 
легко находится по экспериментальным данным
, здесь 
- число ошибочных символов за сеанс связи, 
- число символов переданных за этот сеанс.
К сожалению число реальных каналов, ошибки которых описываются моделью ДСК весьма мало. Это обычно каналы высокого качества локальных сетей. Основное достоинство данной модели – простота и возможность оценки по ней потенциальных границ вероятностных характеристик качества доставки сообщений в системе.
2.6.2 Модель 
В основу построения модели положено понятие плотности ошибок порядка 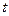. Это неслучайная функция аргументов 
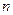и .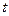
.
В числителе сумма есть среднее число ошибок на блоке длинной 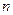, содержащих 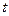или больше ошибок. Значения плотности порядка 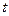ограничены снизу величиной 
, а сверху единицей, т.е. 
. Значения 
не убывают с ростом ; 
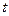и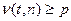 
. По величине плотности 
можно судить о степени группирования ошибок, если считать, что увеличение доли ошибок высших кратностей идентично увеличению степени группирования. Экспериментально установлено, что для многих каналов
, если выполняются условия 
, 
больше хотя бы в несколько раз. Параметр 
носит название показатель группирования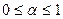 
. Если 
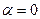, пакетирования нет, имеем канал с независимыми ошибками; 
соответствует каналу с «жестким» пакетированием ошибок.
Достаточно просто доказывается, что
.
Вероятность приема блока ровно с 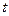ошибками равна 
.
Если использовать приближение 
, то 
, и
.
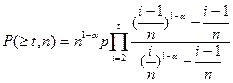На практике обычно применяют еще более простое соотношение
.
Это верхняя граница вероятност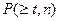и 
. При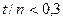 
точные значения 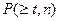близки к верхней границе.
Таким образом, модель задается соотношением 
.
Параметр модели - вероятность ошибки символа, находится как и для канала ДСК.
Параметр находят из уравнения 
. Получаем 
.
Достоинством модели является учет факта пакетирования ошибок, что имеет место в большинстве реальных каналов, возможность единообразно описания разных типов каналов. Так в кабельных каналах значения максимально 
. В КВ радиоканалах минимально 
. Недостаток модели – ее неполнота, остается открытым вопрос о модели на уровне блоков.
Модель на основе ОПП
Наблюдаемое пакетирование ошибок в каналах связи при предположении о пуассоновском характере потока можно объяснить, если считать параметр 
не константой, а случайной величиной или процессом. Получающийся путем рандомизации новый случайный процесс называют обобщенным пуассоновским 
. Будем считать случайной величиной, закон распределения которой известен 
. Тогда канал задается как поток ошибок первым способом:
,
т.е. формула для 
сохраняется, но осуществляется усреднение по параметру.
Поскольку вид и параметры закона распределения для реальных каналов обычно неизвестны, указанной выше формулой воспользоваться не удается.
По экспериментальным данным относительно легко можно найти закон распределения интервалов между ошибками – функцию Пальма-Хинчина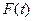 
, которая полностью определяет ОПП (второй способ здания потока).
Используя производящую функцию вероятностей, в [*] доказана формула:
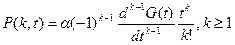
- параметр потока,
и
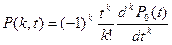
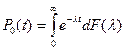- вероятность отсутствия ошибок за время 
. [*]
Таким образом, для ОПП, зная функцию распределения интервалов между ошибками или 
вычисляются вероятности 
, т.е. приходим к заданию потока первым способом но конструктивным.
Рассмотрим один частный случай, когда распределение интервалов задается обобщенной гиперболой
, 
.
Исследование записей потоков ошибок в телефонных каналах показало, что такая ситуация наблюдается довольно часто.
Для параметра потока тогда получается
.
и
.
Наиболее удобна для расчета вероятностей рекуррентная формула:
.
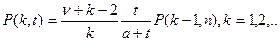
Неизвестные параметры 
и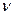 
легко находятся, например, методом моментов, поскольку обобщенная гипербола для интервалов между ошибками приводит к гамма-распределению параметра .
.
Это следует из выражения для
- это преобразование Лапласа-Стильтьеса функции . Зная , получаем 
приведенное выше. Вычисляем по экспериментальны данным среднее число ошибок 
на блоке в бит и второй центральный момент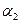 
.
Приравниваем их теоретическим моментам гамма-распределения и из системы уравнений получаем
,
.
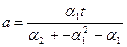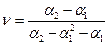На основании полученных значений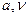 
по модели мы можем найти для любых интервалов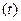 
, т.е. кодовых комбинаций другой значности. Для тропосферного ТЛФ канала при использовании ЧМ сигналов на скорости 1200 получено, например, 
, 
.
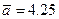Особенно ценно следующее свойство предложенной модели потока ошибок. Многомерное распределение однозначно определяется с помощью одномерного: 
.
Здесь многомерное распределение необходимо для того, чтобы выбирать способ защиты информации от ошибок при передаче по каналам. В частности, чтобы находить вероятности приема сообщения с нескольких повторов.
Недостатки модели – более трудоемкие формулы для расчета, чем у моделей ДСК и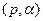 
и тот факт, что не все каналы имеют обобщенную гиперболу в качестве закона распределения между ошибочных интервалов.
