Шаг 0: Приведение к канонической форме.
Шаг 1: Запись всех исходных данных в таблицу.
Шаг 2: Просмотреть столбцы матрицы A и отыскать единичные столбцы с единицами в разных позициях. Соответствующие переменные занести в графу-базис.
Шаг 3: Просматривается базисный столбец, если он заполнен, то переход к алгоритму симплекс-метода.
Конец.
Иначе этап 1.
Этап 1:
Шаг 1: Свободные места в базисном столбце заполняются переменными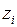 
с номерами соответствующими номерам строк.
Шаг 2: Целевые коэффициенты при переменных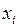 
полагаются равными нулю (
).
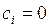Целевые коэффициенты при 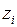полагаются равными минус единице.
Шаг 3: Переход к алгоритму симплекс-метода.
Шаг 4: Если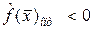 
, то выписывается ответ: Задача несовместна.
Конец.
Иначе переход к этапу 2.
Этап 2:
Шаг 1: Для всех переменных 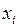целевые коэффициенты полагаются равными 
.
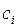Шаг 2: Переход к алгоритму симплекс-метода.
Конец.
Замечание 1: Единичные столбцы, соответствующие переменным 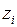в таблицу не заносятся.
Пример 2.5.1. Решить задачу
,
.
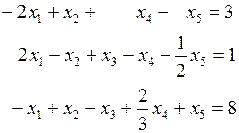
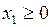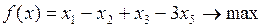1.Занесём все данные задачи в таблицу 2.5.1.
Таблица 2.5.1
| B | c в | x в | -1 | -3 | |||
| 
| 
| 
| 
| |||
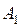
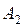
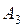
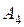
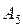
| -2 | -1 | ||||||
| -1 | -1 | -1⁄2 | |||||
| -1 | -1 | 2⁄3 |
- Просматриваем таблицу 2.5.1 и отыскиваем единичные столбцы, для введения их в базис.
В найденной таблице таких столбцов нет, поэтому в графу В ваносят три искусственные переменные, а в графу c в коэффициент (-1).
Таблица 2.5.2.
| B | c в | x в | Ө | |||||
|
|
|
|
|
| ||||
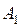
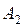
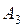
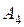
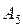
| z 1 | -1 | -2 | -1 | |||||
| z 2 | -1 | -1 | -1 | -1⁄2 | ||||
| z 3 | -1 | -1 | -1 | 2⁄3 |
3. Вычисляем значения целевой функции по формуле: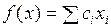 
. Вычисляем оценки по формуле: 
.
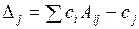Таблица 2.5.3.
| B | c в | x в | Ө | |||||
|
|
|
|
|
| ||||
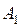
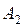
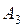
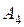
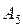
| z1 | -1 | -2 | -1 | |||||
| z2 | -1 | -1 | -1 | -1⁄2 | ||||
| z3 | -1 | -1 | -1 | 2⁄3 | ||||
| -12 | -1 | -1 | -2⁄3 | 1⁄2 |
4. Так как ∆4<0, то x 4 можно ввести в базис.
Вычисляем θ по формуле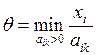 
.
Минимальному значению θ будет соответствовать место направляющего элемента в столбце x 4.
Полностью все шаги перестроения базисного решения представлены в таблице 6.
Таблица 2.5.4.
| B | c в | x в | Ө | |||||
|
|
|
|
|
| ||||
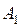
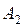
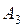
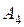
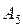
| z 1 | -1 | -2 | -1 | |||||
| z 2 | -1 | -1 | -1 | -1⁄2 | ||||
| z 3 | -1 | -1 | -1 | 2⁄3 | ||||
| -12 | -1 | -1 | -2⁄3 | 1⁄2 | ||||
| x 4 | -2 | -1 | - | |||||
| z 2 | -1 | -3⁄2 | - | |||||
| z 3 | -1 | 1⁄3 | 1⁄3 | -1 | 5⁄3 | |||
| -10 | -1⁄3 | -1⁄3 | -1⁄6 | |||||
| x 4 | -6 | - | ||||||
| z 2 | -1 | -3⁄2 | ||||||
| x 1 | -3 | - | ||||||
| -4 | -1 | 3⁄2 | ||||||
| x 4 | ||||||||
| x 3 | -3⁄2 | |||||||
| x 1 | 1⁄2 | |||||||
Так как все оценк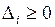и 
и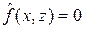 
, то первый этап закончен и переходим ко второму этапу.
Таблица 2.5.5.
| B | c в | x в | -1 | -3 | |||
| А 1 | А 2 | А 3 | А 4 | А 5 | |||
| x 4 | |||||||
| x 3 | -3⁄2 | ||||||
| x 1 | 1⁄2 | ||||||
В верхнюю строку вновь заносим коэффициент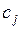 
и в столбец c в коэффициенты 
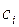при базисных переменных.
Так как все оценки больше или равны нулю, следовательно, получено оптимальное решение
,
.
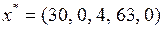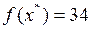Замечание 1. После окончания первого этапа может оказаться, что все оценки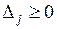 
, значение целевой функции 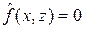, но в базисе сохранились одна или несколько искусственных переменных 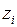, значения, которых равны нулю.
В этом случае непосредственный переход ко второму этапу невозможен, так как во втором этапе искусственные переменные должны отсутствовать. Следовательно, их необходимо исключить из базиса. Для этого просматривается вся строка, соответствующая базисному .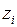
Если вся строка состоит из нулей, то она вычеркивается, и таблица второго этапа будет содержать меньшее число строк, что означает, что ранг исходной матрицы А меньше m.
Если в одной или нескольких строках соответствующих 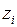присутствуют элементы отличные от нуля, то одна из строк умножается на минус единицу, после этого оценки пересчитываются.
Пример 2.5.2. Пусть после решения задачи первого этапа имеем таблицу 2.5.6. Здесь значение целевой функции ноль, все оценки больше или равны нуля, однако среди базисных переменных присутствуют искусственные.
Таблица 2.5.6.
| B | c в | x в |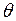 
| ||||
|
|
|
|
| ||||
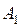
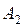
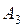
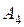
| ---z 1 --- | --- -1 --- | ---- 0 --- | ---- 0 --- | ---- 0 --- | ---- 0 --- | ---- 0 --- | |
| z 2 | -1 | -2 | |||||
| x 1 | -2 | ||||||
| z 3 | -1 | -2 | -1 | ||||
| z 2 | -1 | -2 | |||||
| x 1 | -2 | - | |||||
| z 3 | -1 | -2 | -1 | ||||
| -3 | |||||||
| z 2 | -1 | ||||||
| x 1 | -4 | -1 | - | ||||
| x 4 | -2 | -1 | - | ||||
| -2 | -2 | ||||||
| x 2 | |||||||
| x 1 | |||||||
| x 4 | |||||||
Первая строка вычеркивается, а вторая строка умножается на минус единицу. Затем, используя первый этап алгоритма перестроения базисного решения, находим базис. В результате преобразований искусственные переменные исключены из базиса. Теперь можно переходить ко второму этапу алгоритма перестроения базисного решения.
