3.3. Экономический смысл двойственной задачи
Рассмотрим задачу формирования плана предприятия из первой главы
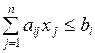 ,
,
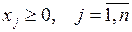 ,
,
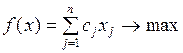 ,
,
где b i – лимит i -го ресурса на предприятии,
a ij – расход i -го ресурса на единицу j -го вида продукции,
c j – прибыль от реализации одной единицы j -го вида продукции,
n – количество изделий которые может выпустить предприятие,
m – количество ресурсов,
x j – количество продукции j -го вида в плане.
Заметим, что задача формирования плана является ЗЛП в симметричной форме, поэтому двойственная к ней задача имеет вид
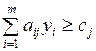 ,
,
 ,
,
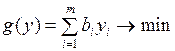 .
.
Для того, чтобы понять экономический смысл двойственности введем наименование всех параметров исходной задачи.
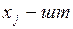 ,
,
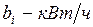 ,
,
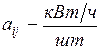 ,
,
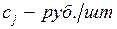 ,
,
и так как в двойственной задачи наименование левой и правой частей должны совпадать
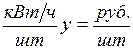 откуда
откуда 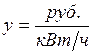 .
.
Таким образом, переменная получает наименование цены единицы ресурса. Однако надо помнить, что двойственная переменная есть цена ресурса только в рамках рассматриваемой задачи, поэтому лауреатом Нобелевской премии Канторовичем Л. В. Двойственные переменные были названы объективно обусловленными оценками. Кроме того так как на оптимальном решении
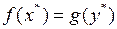 ,
,
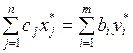 ,
,
то значение двойственной переменной 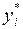 показывает, насколько увеличится суммарная прибыль, если количество соответствующего ресурса увеличится на одну единицу, то
показывает, насколько увеличится суммарная прибыль, если количество соответствующего ресурса увеличится на одну единицу, то 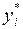 есть мера дефицитности i -го ресурса.
есть мера дефицитности i -го ресурса.
Транспортная задача. Постановка, модель, несбалансированные транспортные задачи, задачи с запретами.
§4. Транспортная задача
4.1. Математическая модель транспортной задачи
Построение транспортной задачи и ее вербальная модель были представлены в первой главе.
Напомним математическую модель транспортной задачи:
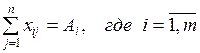 , (1)
, (1)
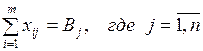 , (2)
, (2)
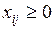 , (3)
, (3)
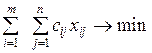 . (4)
. (4)
Ограничение (1) и (2) означают, что от каждого поставщика должна быть вывезена вся продукция, а каждый потребитель должен быть удовлетворен.
Кроме того предполагается выполнение условия баланса
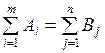 .
.
Как видно из математической модели транспортная задача представляет собой ЗЛП в канонической форме, имеющую (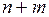 ) ограничений и (
) ограничений и (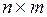 ) переменных. То есть транспортная задача даже при небольшом количестве поставщиков и потребителей оказывается достаточно громоздкой и ее решение с помощью обычного симплекс-метода хотя и возможно, но требует значительных информационных и временных ресурсов. Однако, с учетом специфики системы ограничений, формулы симплекс-метода значительно упрощаются. Модифицированный с учетом структуры матрицы симплекс-метод называется методом потенциалов и будет рассматриваться позже.
) переменных. То есть транспортная задача даже при небольшом количестве поставщиков и потребителей оказывается достаточно громоздкой и ее решение с помощью обычного симплекс-метода хотя и возможно, но требует значительных информационных и временных ресурсов. Однако, с учетом специфики системы ограничений, формулы симплекс-метода значительно упрощаются. Модифицированный с учетом структуры матрицы симплекс-метод называется методом потенциалов и будет рассматриваться позже.
Способ задания
Для решения любой ЗЛП ее необходимо представить в виде таблицы, которую заносят все данные отличающие одну задачу от другой. В частности для ЗЛП общего вида представленной в канонической форме должна быть задана таблица из (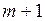 ) строк и (
) строк и (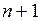 ) столбцов, где в первый столбец
) столбцов, где в первый столбец 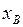 заносятся правые части системы ограничений, а в дальнейшем базисные компоненты текущего базисного решения. В остальные столбцы заносятся столбцы матрицы А, а в первую строку коэффициенты целевой функции.
заносятся правые части системы ограничений, а в дальнейшем базисные компоненты текущего базисного решения. В остальные столбцы заносятся столбцы матрицы А, а в первую строку коэффициенты целевой функции.
Заметим, что условие неотрицательности переменных в таблице не отражается, так как является выполненным для всех ЗЛП. Что же касается транспортной задачи, то 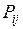 - столбцы ее матрицы ограничений имеют «длину» (
- столбцы ее матрицы ограничений имеют «длину» (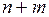 ) и состоят из двух блоков. Первый блок «длины» m имеет единицу на месте i и нули на остальных местах, а второй блок «длины» n имеет единице на месте j и нули на остальных:
) и состоят из двух блоков. Первый блок «длины» m имеет единицу на месте i и нули на остальных местах, а второй блок «длины» n имеет единице на месте j и нули на остальных:
 .
.
Таким образом, если известно число поставщиков и потребителей, то вид столбца 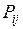 известен и при записи исходных данных его можно не учитывать. Поэтому транспортная задача задается таблицей размера (
известен и при записи исходных данных его можно не учитывать. Поэтому транспортная задача задается таблицей размера (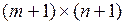 ), где в первом блоке матрицы размером (
), где в первом блоке матрицы размером (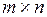 ) выписывается матрица коэффициентов целевой функции
) выписывается матрица коэффициентов целевой функции 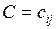 . Справа выписывается столбец со значениями
. Справа выписывается столбец со значениями 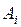 , а внизу -
, а внизу - 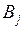 .
.
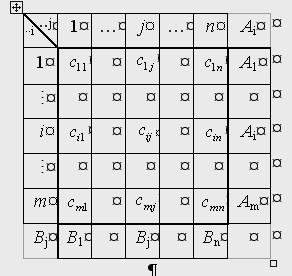
Рис. 1.
Допустимое решение 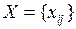 , также заносится в матрицу размером (
, также заносится в матрицу размером (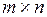 ). При этом i -я строка соответствует i -му ограничению (1), а j -й столбец – j -му ограничению (2) откуда следует, что сумма элементов i -й строки матрицы X равна
). При этом i -я строка соответствует i -му ограничению (1), а j -й столбец – j -му ограничению (2) откуда следует, что сумма элементов i -й строки матрицы X равна 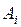 , сумма всех элементов j -го столбца – равна
, сумма всех элементов j -го столбца – равна 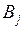 .
.
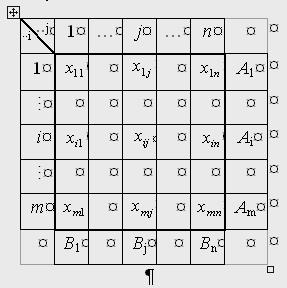
Рис. 2.






