§3. Двойственность в ЗЛП
3.1 Основные понятия и определения
Рассмотрим ЗЛП в канонической форме
 (3.1.1)
(3.1.1)
и ЗЛП в симметричной форме
 (3.1.2)
(3.1.2)
Заметим, что если в канонической форме  , то при записи ЗЛП в симметричной форме условие неотрицательности правых частей не требуется.
, то при записи ЗЛП в симметричной форме условие неотрицательности правых частей не требуется.
Определение 1: Задача
 (3.1.3)
(3.1.3)
называется задачей двойственной к задаче (3.1.1).
Определение 2. Задача
 (3.1.4)
(3.1.4)
называется двойственной к ЗЛП в симметричной форме.
Заметим, что у задачи двойственной к задаче в канонической форме условие неотрицательности переменных отсутствует, в то время как для задачи двойственной к задаче в симметричной форме условие неотрицательности переменных обязательно.
Как следует из вида двойственных задач (3.1.3) и (3.1.4):
1. количество переменных двойственной задачи совпадает с количеством ограничений исходной задачи;
2. количество ограничений двойственной задачи совпадает с количеством переменных исходной задачи;
3. каждому ограничению исходной задачи соответствует переменная двойственной задачи;
4. количество переменных исходной задачи соответствует ограничение двойственной задачи;
5. матрица ограничений двойственной задачи является транспонированной по отношению к матрице ограничений исходной задачи;
6. ограничения двойственной задачи являются неравенствами типа больше или равно;
7. целевые коэффициенты исходной задачи являются правыми частями ограничений двойственной задачи;
8. правые части ограничений исходной задачи являются целевыми коэффициентами двойственной задачи;
9. если в исходной задачи отыскивается максимум целевой функции, то в двойственной – минимум;
10. двойственная задача к двойственной задаче совпадает с исходной.
Исходя из выше сказанного, можно сформулировать правило построения двойственной задачи.
Так как по определению заданы двойственные задачи только к задачам в канонической и симметричной форме, то есть в исходной задаче имеются отклонения от заданных условий, например, имеется неравенство типа больше или равно или целевая функция, стремящаяся к минимуму. Тогда задачу нужно привести к виду описанному ранее. А именно ограничение типа больше или равно заменяется на – меньше или равно и целевая функция стремящаяся к минимуму заменяется на функцию, стремящуюся к максимуму.
Таким образом, алгоритм построения двойственной задачи состоит из двух этапов. На первом этапе задача приводится к виду соответствующему (3.1.1) или (3.1.2), а на втором этапе строится двойственная задача.
Алгоритм построения двойственной задачи
Этап 1:
Шаг 1: Просматриваются ограничения задачи и если среди ограничений имеются ограничения типа больше или равно, то коэффициенты умножаются на минус единицу и знак неравенства изменяется на противоположный.
Шаг 2: Рассматривается целевая функция. Если в исходной задаче требуется найти ее минимум, то все коэффициенты умножаются на минус единицу, а функцию переориентируют на максимум.
Этап 2:
Шаг 1: Каждому ограничению исходной задачи приписывается  , номер которого соответствует номеру ограничения.
, номер которого соответствует номеру ограничения.
Шаг 2: Выписываются в столбик все переменные исходной задачи.
Шаг 3: К каждой переменной  приписывается ограничение двойственной задачи вида
приписывается ограничение двойственной задачи вида 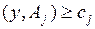 (
( ).
).
Шаг 4: Если ограничение с номером i исходной задачи является неравенством, то в двойственной задаче записывается ограничение вида  .
.
Замечание 1. Если i -е ограничение является неравенством, то условие неотрицательности на соответствующую двойственную переменную не накладывается.
Шаг 5: Выписывается целевая функция двойственной задачи

Пример 3.1. Дана ЗЛП
 (3.1.5)
(3.1.5)
 (3.1.6)
(3.1.6)
 (3.1.7)
(3.1.7)
 ,
,
 .
.
Этап 1. Ограничение задачи (3.1.2) является ограничение типа больше или равно в соответствии с алгоритмом его необходимо заменить на ограничение – меньше или равно.
Целевая функция ориентирована на минимум, в соответствии с алгоритмом ее необходимо заменить на функцию ориентированную на максимум.
Окончательный вид задачи для которой будет строить двойственная следующий
 (3.1.5)
(3.1.5)
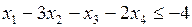 (3.1.6)
(3.1.6)
 (3.1.7)
(3.1.7)
 ,
,
 .
.
Этап 2.
Каждому ограничению приписываем двойственную переменную 

| 
| (3.1.5) |

| 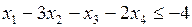
| (3.1.6) |

| 
| (3.1.7) |
 ,
,
 .
.
Выписываются все переменные двойственной задачи и к ним приписываются ограничения двойственной
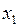
| 
|
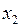
| 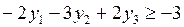
|

| 
|

| 
|
В соответствии с алгоритмом условие типа  накладывается напервую и вторую двойственную переменную:
накладывается напервую и вторую двойственную переменную: 
Целевая функция двойственной задачи имеет вид
 .
.
Окончательный вид двойственной задачи следующий
 ,
,
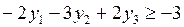 ,
,
 ,
,
 ,
,
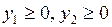 ,
,
 .
.






