Вербальная модель
Для составления дневного рациона имеем в наличии n различных кормов. Для получения сбалансированного рациона (белки, витамины, микроэлементы и др.) необходимо чтобы в него входило m различных ингредиентов, причем каждый i -й ингредиент должен входить в количестве не меньше b i (
), a ij – количество i -го ингредиента в одной единице j -го вида корма, c j – стоимость одной единицы j -го корма.
Требуется сформировать ежедневный рацион, так чтобы он был обеспечен всеми необходимыми ингредиентами и имел минимальную стоимость.
Математическая модель
Введем вектор 
- рацион, где x j – количество j - го вида корма в рационе.
По аналогии с предыдущей задачей математическая модель задачи формирования рациона будет иметь вид
, (1.3.2.1)
, (1.3.2.2)
(1.3.2.3)
Заметим, что полученная математическая модель недостаточно адекватно отражает искомую цель, т.к. в вербальной модели описаны не все необходимые зависимости.
В самом деле, если предположить, что среди выбранных кормов присутствует, например, прошлогодняя солома, стоимость которой равна нулю, а все имеющиеся ингредиенты присутствуют в ней в исчезающее малых количествах, то при решении задачи может получиться, что ежедневный рацион должен состоять только из прошлогодней соломы и составлять, например, пятнадцать тонн, что, разумеется, невозможно.
Отсюда следует, что ограничение (1.3.2.2) необходимо заменить на 
, где D – вектор верхних границ переменных x j.
Задание для самостоятельной работы
Если (1.3.2.1)-(1.3.2.3) оставить в исходном виде, то какие еще «неприятности» мы можем еще получить в оптимальном плане?
Транспортная задача
Вербальная модель
Имеется m поставщиков некоторого продукта. A i () – количество продукта у i -го поставщика.
Имеется n потребителей этого продукта. B j (
) – потребность j -го потребителя.
с ij – затраты на перевозку единицы продукта (1т, 1кг, 1 банки и т.д.) от i -го поставщика к j -му потребителю.
Требуется составить план перевозки продукции от поставщиков к потребителям так, чтобы суммарные затраты на перевозку были минимальными (имеется ввиду, что перевозки осуществляет одна фирма).
Предполагается выполнение условия баланса:
,
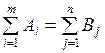то есть суммарное наличие продукта у всех поставщиков равно суммарной потребности всех потребителей.
Математическая модель
Пусть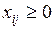 
– количество продукции, которое перевозят от i -го поставщика к j –му потребителю.
Так как есть условие баланса 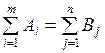, то возникают ограничения:
1) От каждого поставщика должна быть вывезена вся продукция
.
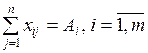2) Каждый потребитель должен быть удовлетворен, т.е. должно быть перевезено столько продукции, сколько нужно, ни больше, ни меньше.
.
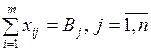Целевая функция будет выглядеть следующим образом:
.
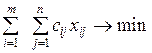