Схема корреляционного обнаружителя одиночного сигнала с полностью известными параметрами. Сжатие сигнала по спектру

 

Переходя от дискретного к непрерывному времени, логарифм отношения правдоподобия можно представить в виде:

 

 

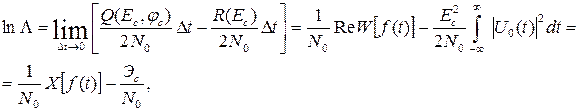
где 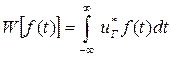- корреляционный интеграл,

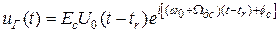- опорный сигнал.

Решение о наличии сигнала можно принимать, формируя квадратур­ную составляющую корреляционного интеграла, монотонно связанную с отношением правдоподобия, и сравнивая ее с порогом:

 

.

 

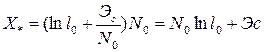Схема соответствующего корреляционного обнаружителя показана на рис. 3.1.

 

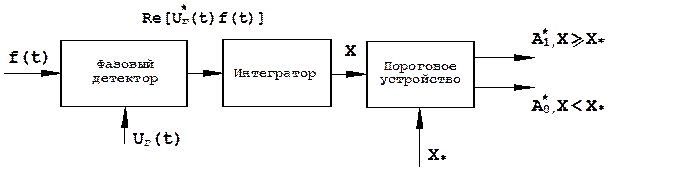Рис. 3.1. Корреляционный обнаружитель одиночного сигнала с полностью известными параметрами.

 

Квадратурная составляющая корреляционного интеграла формируется путем скалярного перемножения принятого и опорного сигналов и последующего интегрирования этого произведения. Роль скалярного перемножителя выполняет, фазовый детектор. Опорный сигнал формируется с учетом знания всех периметров принимаемого сигнала: закона модуляции, времени запаздывания, несущей частоты, ее доплеровского смещения, фазы, амплитуды.

На рис. 3.2 показаны эпюры, поясняющие работу корреляционного обнаружителя (на примере пятиэлементного кода Баркера). После перемножения принятого и опорного сигналов происходит демодуляция полезного сигнала, т.е. устранение его внутриимпульсной фазовой или частотной модуляции:

 

 

 

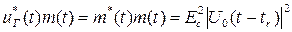
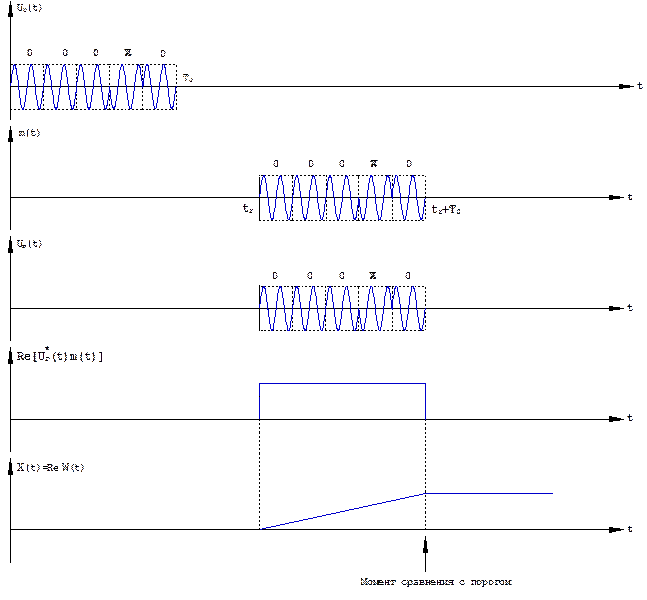Рис. 3.2. Пояснение работы корреляционного обнаружителя одиночного сигнала с полностью известными параметрами.

 

На выходе фазового детектора формируется видеоимпульс, форма которого определяется квадратом амплитудного закона модуляции сигнала. Ширина спектра демодулированного сигнала становится обратно пропорцио­нальной длительности сигнала Δ F = 1/ T _0, т.е. происходит сжатие сигнала по спектру, причем коэффициент сжатие оказывается равным базе сигнала:

 

K_сж = Δf₀ / ΔF = Δf₀·T₀.

 

Напряжение на выходе интегратора в течение длительности сигнала увеличивается: идет процесс накопления энергии сигнала. В конце длительности сигнала, когда напряжение на выходе коррелятора (сочетание перемножителя и интегратора) достигает максимального уровня, должно осуществляться его сравнение с порогом и, приниматься решение о наличии или отсутствии сигнала. Следует заметить, что управление порогом Х _* при изменении энергии сигнала Э _с и спектральной плотности помехи N ₀ осуществляется так, что при соответствующих изменениях условных вероятностей D и F обеспечивается их максимальная взвешенная разность
D – l ₀ F, а следовательно минимальный средний риск R.

 

3.3. Схемы корреляционных обнаружителей одиночного сигнала с неизвестной начальной фазой. Эффект «слепой фазы» и способы его устранения

 

Описанная выше схема корреляционного обнаружителя одиночного сигнала с полностью известными параметрами имеет лишь теоретическое значение. В действительности амплитуда и фаза принятого сигнала априорно неизвестны. В связи с этим найдем усредненное по начальной фазе отношение правдоподобия, учитывая при этом, что начальная фаза равномерно распределена на интервале от - π до π радиан. Для этого вначале величину Q (E _c, φ _c), монотонно связанную с отношением правдоподобия, представим в виде, отражающем яв­ную функциональную связь с начальной фазой принятого сигнала:

 

 

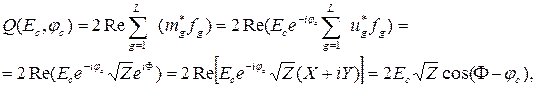
где

 

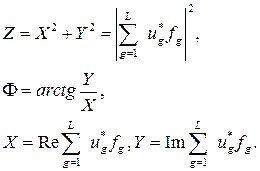
Усредненное по начальной фазе принятого сигнала отношение правдоподобия приобретает вид:

 

 

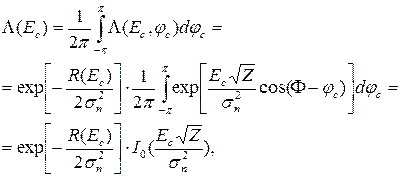
где 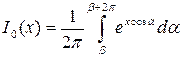- модифицированная функция Бесселя нулевого порядка, являющаяся монотонно возрастающей функцией своего аргумента (рис. 3.3).

 

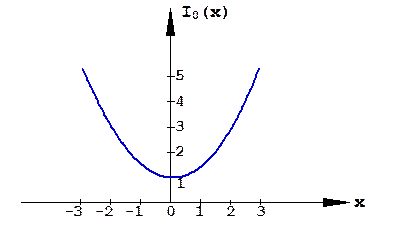
Рис. 3.3. Модифицированная функция Бесселя нулевого порядка.

 

Из полученного выражения следует, что решение о наличии сигнала может быть принято по величине Z, которая после перехода от дискретного времени к непрерывному оказывается квадратом модуля корреляционного интеграла

 

,

 

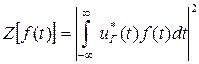где 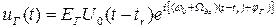- опорный сигнал, амплитуда и фаза которого (E _г, φ _г) не связаны с амплитудой и фазой принятого сигнала (E _c, φ _c).

Существует два варианта схемной интерпретации математических операций над принятым сигналом f (t), содержащихся в полученном выражении.

Первый вариант сводится к корреляционной обработке на некоторой радиочастоте ω _пр. Это означает, во-первых, смещение опорного сигнала по частоте на промежуточную частоту:

 

,

 

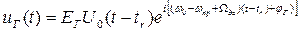во-вторых, перемножение принятого и опорного сигнала, с помощью смесителя-перемножителя, в результате которого происходит внутриимпульсная демодуляция полезного сигнала, т.е. устранение внутриимпульсной фазовой или частотной модуляции, и формирование радиоимпульса на промежуточной частоте, форма которого определяется квадратом амплитудного закона модуляции сигнала:

 

,

 

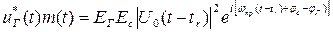и, в-третьих, интегрирование демодулированного и сжатого по спектру сигнала (К _сж = Δ f ₀ · T ₀) на радиочастоте с помощью идеального радиоинтегратора, импульсная характеристика которого, т.е. отклик на дельта-функцию, представляет собой незатухающее колебание на промежуточной частоте (рис. 3.4):

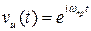, t > 0.

 

 

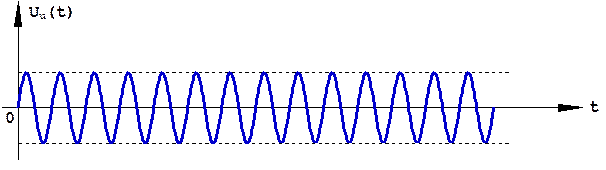
Рис. 3.4. импульсная характеристика идеального радиоинтегратора.

 

При этом квадрат модуля корреляционного интеграла представляется в виде:

 

.

 

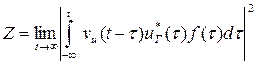Схема корреляционного обнаружителя одиночного сигнала с неизвестной начальной фазой на радиочастоте показана на рис. 3.5.

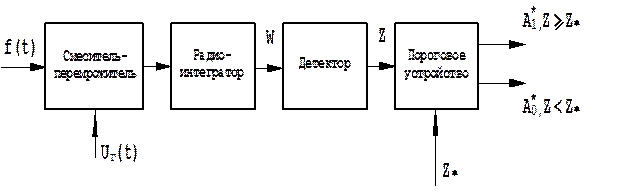Рис. 3.5. Корреляционный обнаружитель одиночного сигнала с неизвестной начальной фазой и обработкой на радиочастоте.

 

Эпюры сигналов, поясняющие работу корреляционного обнаружителя с обработкой на радиочастоте, показаны на рис. 3.6.

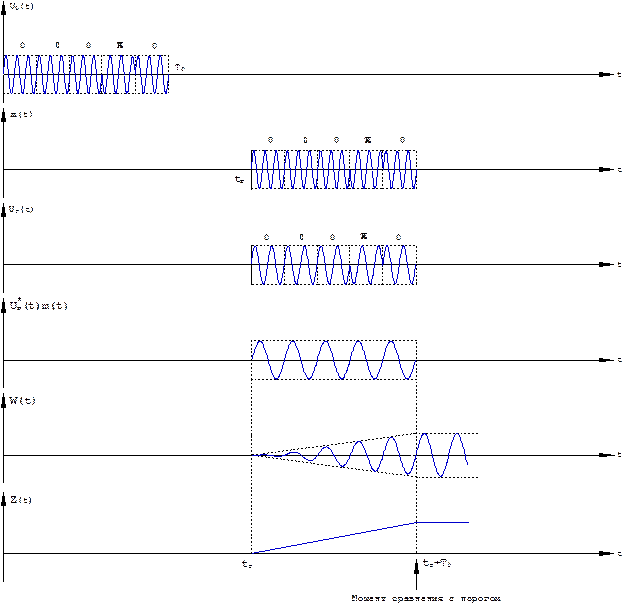
Рис. 3.6. Пояснение работы корреляционного обнаружителя одиночного сигнала с неизвестной начальной фазой и обработкой на радиочастоте.

 

Заметим, что в условиях априорной неопределённости (т.е. незнания) амплитуды сигнала, формирование порога, обеспечивающего максимум взвешенной разности D – l ₀ F или минимум среднего риска R, принципиально невозможно. В этом случае порог Z _* формируют, исходя из некоторой фиксированной достаточно малой условной вероятности ложной тревоги F =const<<1. В реальных условиях не существует идеальных радиоинтеграторов и вместо них используются узкополосные фильтры на промежуточной частоте, импульсная характеристика которых, т.е. отклик на дельта-функцию представляет собой затухающее колебание (рис. 3.7):

 

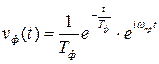, t > 0,

 

где Т _ф = 1/2Δ f _ф - постоянная времени узкополосного фильтра, обратно пропорциональная удвоенной полосе пропускания.

 

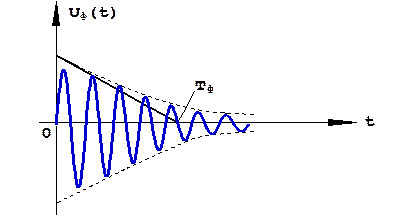
Рис. 3.7. Импульсная характеристика узкополосного фильтра.

 

Чтобы характеристики корреляционного обнаружителя с узкополосным фильтром заметно не уступали оптимальному корреляционному обнаружителю с идеальным радиоинтегратором, достаточно выполнения условия: Т _ф>> Т ₀.

Амплитуда колебания на выходе узкополосного фильтра достигает максимального значения в момент времени t = t_r + Т ₀,т.е. в конце сигнала, когда заканчивается накопление его энергии, после чего амплитуда этого колебания начинает уменьшаться. Поэтому сравнение с порогом выходного сигнала устройства обработки Z (t), тем более, необходимо осуществить без задержки в момент времени t = t_r + Т ₀ .

Второй вариант схемного построения корреляционного обнаружителя одиночного сигнала с неизвестной начальной фазой сводится к обработке на видеочастоте с двумя квадратурными каналами. Действительно, представляя квадрат модуля корреляционного интеграла суммой квадратов его действительной и мнимой частей

 

,

 

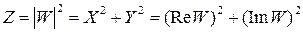где , ,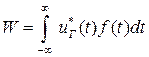

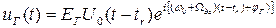приходим к схеме корреляционной обработки с двумя каналами, отличающимися фазовым сдвигом опорных сигналов на π/2 радиан и поэтому называющимися квадратурными (рис. 3.8):

 

,

.

 

 

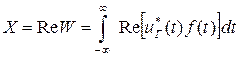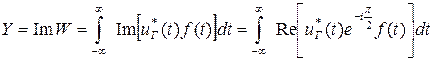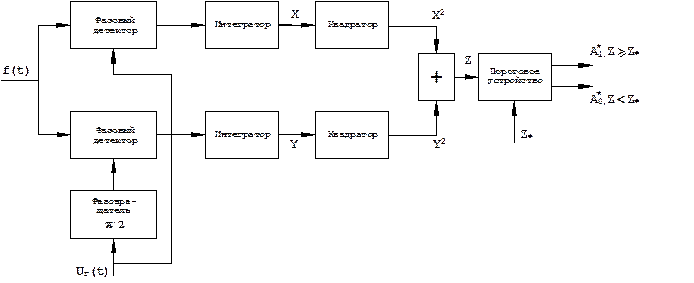Рис. 3.8. Корреляционный обнаружитель одиночного сигнала с неизвестной начальной фазой на видеочастоте с двумя квадратурными каналами.

 

Роль скалярных перемножителей в каналах выполняют фазовые детекторы. Роль интеграторов могут выполнять апериодические RC - цепочки, постоянная времени которых Т _ф = RC много больше длительности сигнала (Т _ф>> Т ₀), роль квадраторов могут выполнять двухполупериодные выпрямители.

Рассмотренные варианты схемного построения корреляционного обнаружителя одиночного сигнала с неизвестной начальной фазой устраняют так называемый эффект «слепой фазы». Суть этого эффекта состоит в потере сигнала при неблагоприятном соотношении фаз принятого φ _с и опорного φ _г сигналов. Если эти фазы отличаются на ±π радиан, т.е. если принятый и опорный сигналы являются взаимно ортогональными, то их скалярное произведение на выходе фазового детектора будет равно нулю. Следовательно, в таком случае при одноканальном построении корреляционного обнаружителя с обработкой на видеочастоте (рис. 3.1) имел бы место эффект «слепой фазы». Схемы корреляционных обнаружителей, показанные на рис. 3.5 и рис. 3.8, лишены этого недостатка. В первом случае (рис. 3.5) при одноканальной корреляционной обработке на радиочастоте после внутриимпульсной фазовой или частотной демодуляции принятого сигнала формируется радиоимпульс на промежуточной частоте и его начальная фаза φ _с - φ _г не играет никакой роли в процессе дальнейшего накопления его энергии на радиоинтеграторе. Во втором случае (рис. 3.8) при двухканальной корреляционной обработке на видеочастоте амплитуда демодулированного сигнала (с учётом полярности) на выходе фазового детектора в первом канале пропорциональна cos(φ _с - φ _г), а во втором канале sin(φ _с - φ _г), и после соответствующего объединения этих каналов сигнальная составляющая становится инвариантной к соотношению фаз принятого и опорного сигналов, поскольку cos²(φ _с - φ _г)+ sin²(φ _с - φ _г)=1.

Таким образом, эффект «слепой фазы» может быть преодолен одним из двух способов: либо с помощью одноканальной корреляционной обработки на радиочастоте (рис. 3.5), либо с помощью двухканальной корреляционной обработки, на видеочастоте (рис. 3.8) с двумя квадратурными каналами.