В результате процесса обнаружения должно быть принято решение о наличии или отсутствии сигнала:
- решение А *1 есть сигнал,
- решение А *0 - нет сигнала.
Эти решения могут быть приняты при двух взаимно исключающих условиях, которые при выработке решения неизвестны:
- условие А 1 - есть сигнал,
- условие А 0 - нет сигнала.
При обнаружении возможны 4 ситуации совмещения случайных событий "решения" и "условия":
- ситуация А *1 А 1- правильное обнаружение,
- ситуация А *0 А 1 - пропуск сигнала,
- ситуация А *1 А 0 - ложная тревога,
- ситуация А *0 А 0 - правильное необнаружение.
Каждому решению соответствует некоторая плата - цена Cjk:
- цена правильного обнаружения C 11,
- цена пропуска сигнала C 01,
- цена ложной тревоги C 10,
- цена правильного необнаружения C 00.
Естественно считать, что цена любого ошибочного решения больше цены соответствующего правильного решения:
C 01 > C 11, C 10 > C 00.
Более того, цена правильных решений должна быть отрицательной:
C11 < 0, C00 < 0.
Действительно, если за ошибочные решения наблюдатель должен расплачиваться, то за правильные решения он должен вознаграждаться. В этом и состоит смысл отрицательной цены правильных решений.
При обнаружении хотелось бы обеспечить и максимальные вероятности правильных решений (правильное обнаружение, правильное необнаружение), и минимальные вероятности ложных решений (пропуск сигнала, ложная тревога). Однако эти требования противоречивы. Чтобы обеспечить разумный компромисс, выбирают такое правило решения, при котором для совокупности всех возможных ситуаций обеспечивались бы наилучшие результаты, т.е. правило решения должно быть оптимальным в среднем, статистически. Для этого вводят понятие среднего риска (средней платы), который является взвешенной суммой цен (плат) всех ситуаций, причём весовыми коэффициентами являются вероятности этих ситуаций:
R = C 11· P (А *1 А 1) + C 01· P (А *0 А 1) + C 10· P (А *1 А 0) + C 00 P (А *0 А 0).
Наилучшей или оптимальной системой обнаружения будем считать такую, которая обеспечивает минимум среднего риска.
Известно, что вероятность совместного наступления событий А и В, записываемая как Р (АВ), может быть представлена через априорные и условные вероятности этих событий:
Р (АВ) = Р (А)· Р (В / А) = P (B)· P (A / B).
Следовательно, средний риск может быть представлен следующим образом:
R = C 11· Р (А 1)· P (А *1/ А 1) + C 01· Р (А 1)· P (А *0/ А 1) + C1 0· Р (А 0)· P (А *1/ А 0) +
+ C 00· Р (А 0)· P (А *0/ А 0).
Условные вероятности, представленные в данном выражении, носят в статистической теории обнаружения специальные названия и имеют специальные обозначения:
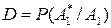- условная вероятность правильного обнаружения, т.е. вероятность принять решение о наличии сигнала, когда сигнал есть;
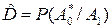- условная вероятность пропуска сигнала, т.е. вероятность принять решение об отсутствии сигнала, когда - сигнал есть;
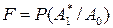- условная вероятность ложной тревоги, т.е. вероятность принять решение о наличии сигнала, когда сигнала нет;
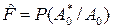- условная вероятность правильного необнаружения, т.е. вероятность принять решение об отсутствии сигнала, когда сигнала нет.
Поскольку соответствующие одному и тому же условию А 1 или А 0 решения А *1 и А *0 взаимно исключающие, то
, 
.
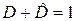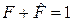Отметим также, что наличие и отсутствие сигнала составляют полную группу событий, так что априорные вероятности этих событий удовлетворяют условию
Р (А 1) + Р (А 0) = 1.
С учетом введённых обозначений выражение среднего риска можно представить в виде
R = C 01· Р (А 1) - D · P (А 1)(C 01 - C 11)+ C 00· Р (А 0) + F · P (А 0)(C 10 - C 00 ) =
= C 01· Р (А 1) + C 00· Р (А 0) - Р (А 1)(C 10 - C 11)(D - l 0 F),
где
.
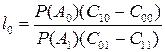Полученное выражение свидетельствует о том, что минимуму среднего риска соответствует максимум взвешенной разности условных вероятностей правильного обнаружения и ложной тревоги min R → max(D – l 0 F), причём весовой множитель l 0 зависит от априорных вероятностей наличия и отсутствия сигнала и соотношения цен (плат) за правильные и ошибочные решения.
