Вернемся к схеме замещения рис. 1.5, на которой показаны три независимые контуры и принятые положительные направления обхода этих контуров. Без доказательства, которое базируется на уравнениях второго закона Кирхгофа и закона Ома [1], рассмотрим матричное выражение системы контурных уравнений:
. (1.25)
Здесь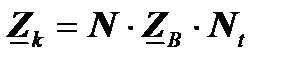 
— квадратная неособенная матрица порядка k, называемая матрицей контурных сопротивлений, где k — число независимых контуров, определяемое как k =m-n, m — число ветвей, n — число независимых узлов.
Как видно, использование системы контурных уравнений также позволяет сократить порядок решаемой системы уравнений.
В (1.25) 
— матрица – столбец контурных токов;
Е к — матрица – столбец контурных ЭДС.
Остальные обозначения такие же, что при записи уравнений законов Кирхгофа (см. п. 1.5).
Формируется и решается система контурных уравнений (1.25), находятся токи контуров 
, а по ним — токи ветвей
. (1.26)
Затем рассчитываются напряжения в узлах и мощности ветвей.
Дерево и хорды графа
Вернемся к направленному графу схемы замещения рис. 1.5.
В направленном графе удобно ветви разделить на две группы:
дерево графа и хорды.
1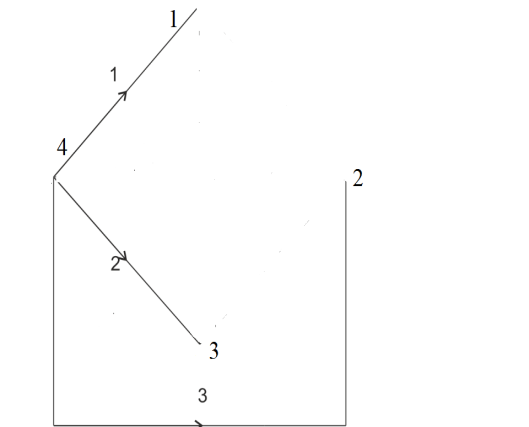 
2 
Рис. 10 Возможные варианты деревьев графа, показанного выше
Дерево графа — это подграф, состоящий из совокупности минимального числа ветвей, которые соединяют все узлы. Дерево графа — это подграф, который не содержит замкнутых контуров. На рис.10.1 ветви 1,2,3 составляют дерево графа, остальные ветви называются хордами. Деревьев можно выделить много, оно не единственное, на рис 10.2 — ветви 1, 2,4 составляют другое дерево графа.
Число ветвей дерева равно числу независимых узлов, а число хорд равно числу независимых контуров. Из множества деревьев выделим дерево, ветвям которого присвоены первые номера (дерево рис 10.1). Для приведенного выше графа составим первую матрицу соединений М. Проведём в ней перегородку, выделив столбцы, соответствующие ветвям дерева 1, 2, и 3. В результате матрица М может быть представлена как клеточная матрица – строка, элементы которой — матрицы 
и 
.
(1.27)
1 2 3 4 5 6
Ветви дерева хорды
Заметим, что матрица , определяющая, как ветви дерева связаны с узлами, всегда квадратная, так как число ветвей дерева равно числу независимых узлов, и, следовательно, может быть обращена. Матрица 
фигурирует в контурном уравнении (1.25) и в выражении для токов ветвей (1.26).
Метод контурных токов в программных комплексах для расчетов установившихся режимов используется редко, из – за сложности и неоднозначности выделения независимых контуров.
