УРАВНЕРИЯ УСТАНОВИВШЕГОСЯ РЕЖИМА СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ В МАТРИЧНОЙ ФОРМЕ
Основные сведения об ЭЭС и ее режимах.
В данном разделе курса рассматриваются электротехнические и математические основы методов и алгоритмов, реализуемых в виде программных комплексов для расчетов установившихся режимов СЭС на ПК.
Под системой электроснабжения (СЭС) будем понимать электроэнергетическую систему (ЭЭС), т.е. совокупность элементов, вырабатывающих (генераторы), преобразующих (трансформаторы, преобразователи), передающих, распределяющих (линии передач) и потребляющих электрическую энергию (двигатели, различные электротехнологические установки, освещение и т.д.).
Рассмотрим упрощенную (без коммутационных аппаратов) схему участка системы:
Рис. 1.1. Принципиальная схема участка системы электроснабжения.
На рис.1.1 индекс э означает эквивалентный генератор (Г) или трансформатор (Т), мощность которого равна сумме полных мощностей блоков или сумме мощностей, как правило, двух трансформаторов на понижающих подстанциях. Трансформаторы Тэ-1 и Тэ-2 – повышающие, Тэ-3 и Тэ-4 – понижающие, 
- воздушные линии (ВЛ).
При расчете режимов можно исключить из рассмотрения понижающие и повышающие трансформаторы, найдя расчетные мощности в узлах 1, 2, 3 и 4 путём добавления к мощностям нагрузок на шинах10(6) кВ потерь мощности в трансформаторах Тэ-3, Тэ-4 и вычитания из мощностей генераторов потерь мощности в трансформаторах Тэ-1, Тэ-2. В результате мы получаем простейшую электрическую систему одного номинального напряжения.
Рис.1.2. Принципиальная упрощенная схема участка системы электроснабжения.
На рис.1.2 
– расчетные нагрузки подстанций, узел 1- базисный и балансирующий, узлы 1 и 2 – генераторные, 3,4 – нагрузочные.
Режимом системы называется совокупность процессов, существующих в ней и определяющих её состояние в любой момент времени или на некотором интервале времени.
Режим характеризуется т.н. параметрами режима – показателями, количественно определяющими условия работы системы. Это:
|
|
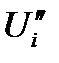
· напряжения в узлах, которые в зависимости от формы их представления записываются как:
,
в полярной системе координат (в показательной форме), 
, 
- общее число узлов, включая базисный, как правило, совпадающий с балансирующим узлом, n - число независимых узлов,
|
|
,
в прямоугольной системе координат (в алгебраической форме).
Рис.1.3. Определение вектора напряжения 
на комплексной плоскости.
На рис. 3: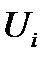 
-модуль вектора напряжения , длина которого равна его действующему значению;
- фаза вектора напряжения, т.е. угол между положительным направлением этого вектора и положительным направлением действительной оси комплексной плоскости;
-действительная часть комплекса напряжения;
-мнимая часть комплекса напряжения.
· Токи ветвей 
, 
, m – число ветвей.
· Мощности в узлах
, откуда 
.
Здесь 
− полная или кажущаяся мощность, 
− активная и 
− реактивная мощности в узле i.
· Мощности в начале 
и конце 
каждой ветви, .
· Потери мощности в ветвях и во всей системе.
Параметры режима связаны между собой соотношениями, в которые входят параметры системы – показатели, количественно определяемые физическими свойствами элементов системы, схемой их соединения и рядом допущений расчетного характера:
· Сопротивления ветвей 
, Ом.
· Проводимости ветвей 
, Сименс.
· Собственные и взаимные проводимости узлов (узловые проводимости)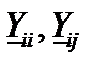 
.
· Коэффициенты трансформации.
Различают:
· Нормальный установившийся режим (принимают допущение, что в установившемся режиме параметры режима не изменяются).
· Послеаварийный установившийся режим (какой-то элемент − линия, трансформатор отключились).
· Ремонтный установившийся режим.
· Переходный режим (кратковременный), во время которого система переходит от одного состояния к другому, при этом параметры режима изменяются.
Установившиеся режимы с математической точки зрения описываются системой алгебраических уравнений, в то время как переходные режимы – системой дифференциальных уравнений.
