1. По матрице М можно однозначно восстановить конфигурацию соответствующей ей схемы, т.е. матрица содержит исчерпывающую информацию о направленном графе схемы замещения (в том числе и необходимую для составления матрицы N).
Матрица N в общем случае не содержит полной информации о конфигурации рассматриваемой схемы, так как разомкнутые части схемы в ней не отражаются.
2. Для разомкнутых сетей вместо первой матрицы соединений, или матрицы Т, может вводиться одномерный массив номеров узлов, которые являются началами ветвей, если номер ветви соответствует номеру узла, являющегося её концом.
Ветви
В общем случае, когда вводится информацию по ветвям, то для каждой ветви вводятся:
· номер узла начала ветви 
;
· номер узла конца ветви 
.
Кроме того, вводится информация о параметрах элементов схемы замещения каждой ветви.
| Номер узла начала
| Номер узла конца 
| 
| 
| 
| 
|
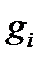
Каждая строка соответствует отдельной ветви.
1.5.5 Обобщенное уравнение законов Кирхгофа. «Прямой» метод определения токораспределения.
Первый закон Кирхгофа в матричном виде записывается как:
,
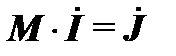причем после линеаризации (внешней итерации) это матричное уравнение линейно. С другой стороны, система линейных алгебраических уравнений в матричном виде записывается как:
.
Решение в матричном виде можно записать как:
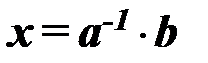(1.14)
Если считать, что вектор x – есть вектор (матрица-столбец) токов ветвей 
, то возникает вопрос: нельзя ли воспользоваться уравнением только 1-го закона Кирхгофа, чтобы по информации о конфигурации сети и о токах в узлах найти токи ветвей? В общем случае этого сделать нельзя, т.к. первая матрица соединений М – прямоугольная матрица, а обращать можно только квадратные матрицы. Но есть частный случай — разомкнутые сети, для которых это сделать можно. Они представляют для нас интерес, поскольку распределительные сети промышленных предприятий городов и сельских районов, как правило, работают в разомкнутом режиме с целью ограничения токов короткого замыкания.
Особенности определения токораспределения в разомкнутых сетях: его можно выполнить просто, воспользовавшись матрицами М или Н.
Для разомкнутых сетей матрица М – квадратная, а, следовательно, её можно обратить, если определитель этой матрицы отличен от нуля.
Разомкнутые сети бывают радиальные (Рис 1.7) и магистральные (Рис 1.8).
Рис 1.7 Схема разомкнутой радиальной электрической сети
Для схемы рис. 1.7 в качестве базисного и балансирующего принимается узел с номером 0, т.е. узел, к которому подключен источник питания. Для данной схемы первая матрица соединений имеет вид:
независимые узлы
ветви.
Поскольку она квадратная, её можно обратить и, представив нагрузки в узлах задающими токами, найти токи в ветвях согласно (1.14):
.
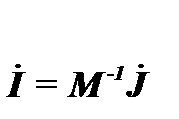В развернутом виде:
.
Из схемы рис. 1.7 видно, что в результате получено действительное токораспределение, токи ветвей равны:
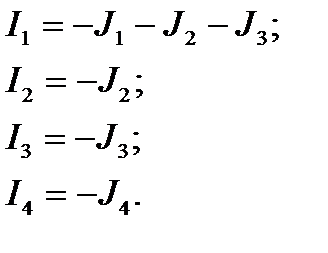
Знак минус перед задающими токами обусловлен тем, что все узлы —нагрузочные, и для них задающие токи равны токам нагрузки, взятым со знаком минус.
Рис. 1.8 Разомкнутая магистральная электрическая сеть
Рис. 1.9 Направленный граф для схемы рис 1.8
Для графа рис. 1.9 первая матрица соединений при условии, что в качестве базисного и балансирующего взят узел 0, к которому подключен источник питания, имеет вид:
Матрица, обратная матрице М, называется матрицей токораспределения С.
.
Из 1-го закона Кирхгофа находим токораспределение:
.
(1.15)
Аналогично, пренебрегая потерями мощностей в ветвях, можно найти мощности ветвей по известным мощностям в узлах (приближенное потокораспределение):
.
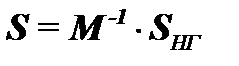Токораспределение в разомкнутой сети можно найти также, воспользовавшись матрицей ребра – пути Н.
Для магистральной схемы рис. 1.8:
-матрица токов ветвей;
-матрица нагрузки в узлах.
Токораспределение в схеме находим как
.
В развернутом виде
Сопоставим это выражение с выражением (1.15), они совпадают.
Нетрудно заметить, что если нагрузка задана во всех узлах, между матрицами Н и М соблюдается соотношение:
.
| Матрица-столбец контурных ЭДС |
| Матрица-столбец токов ветвей |
| Матрица соединений ветвей в независимые контуры |
Найти из этого выражения токи ветвей также в общем случае нельзя, т.к. матрица 
прямоугольная, поскольку её размерность определяется как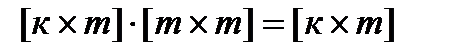 
.
Для определения токораспределения в сети произвольной конфигурации вспомним о существовании клеточных матриц и образуем клеточную матрицу – столбец, состоящую из 2-х клеток. Первая клетка — это матрица соединений М, а вторая — произведение второй матрицы соединений на матрицу сопротивлений ветвей. Умножим справа эту матрицу на матрицу токов ветвей I. Произведение строк матрицы М на столбец матрицы токов ветвей дает согласно первому закону Кирхгофа задающие токи Ji в соответствующих узлах, а произведение строк матрицы на столбец матрицы токов ветвей дает согласно второму закону Кирхгофа контурные ЭДС Еki. В результате произведение представляет собой клеточную матрицу – столбец, первый элемент которой — это матрица – столбец задающих токов, а второй — матрица столбец контурных ЭДС.
| Независимые контуры |
| Независимые узлы |
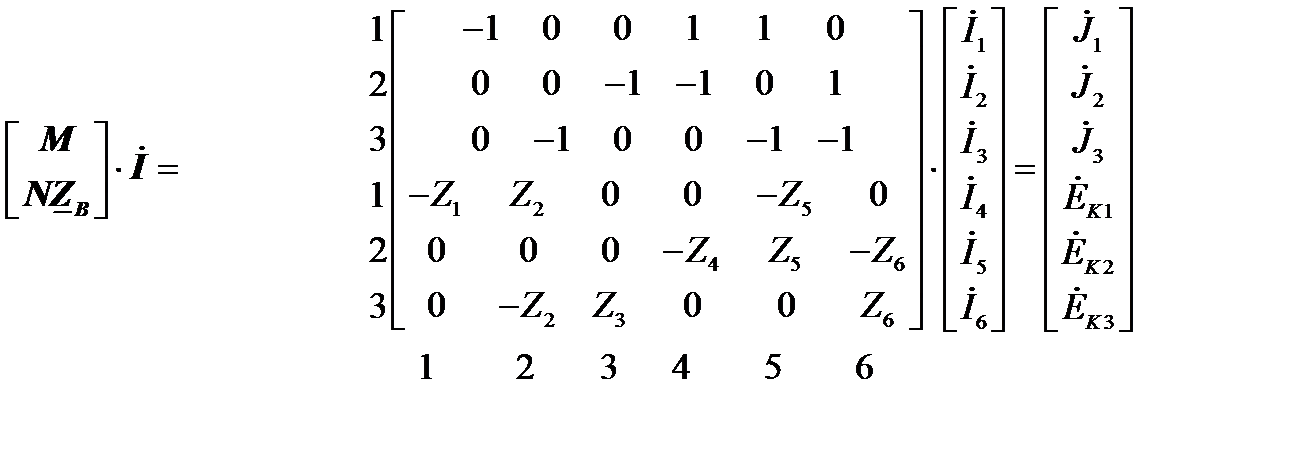(1.16)
| Ветви |
Матрица 
- всегда квадратная, т.к. число строк в ней равно 
- числу ветвей. Число столбцов тоже равно m, т.е. это квадратная матрица 
порядка m, и, следовательно, её можно обратить и найти токораспределение в схеме согласно (1.14). В результате получаем обобщенное уравнение законов Кирхгофа, которое в компактной форме записи выглядит так:
(1.17)
- это нелинейное уравнение, его вид не зависит от конфигурации сети и числа её элементов.
Недостатки обобщенного уравнения законов Кирхгофа и метода нахождения токораспределения, который основывается на этом уравнении:
1. Высокий порядок решаемого матричного уравнения, который определяется числом ветвей, что обуславливает громоздкость расчетов. Для замкнутых сетей произвольной конфигурации число ветвей больше числа узлов в среднем в полтора раза (
).
2. Трудности при автоматизированном формировании этого уравнения, вытекающие из сложности и неоднозначности выделения независимых контуров.
Поэтому на практике применяются методы, в которых порядок решаемых матричных уравнений ниже: метод узловых уравнений, метод контурных токов.
