Число независимых контуров для схемы любой конфигурации определяется из выражения:
,
где m - число ветвей, n - число независимых узлов, 
- число независимых контуров.
Согласно второму закону Кирхгофа, сумма падений напряжений в сопротивлениях ветвей, составляющих независимые контуры, должна быть равна алгебраической сумме ЭДС, входящих в соответствующий контур. Для схемы замещения Рис 1.5 имеем 
.
Обозначим: 
- падение напряжения в сопротивлении ветви j;
-контурная ЭДС первого контура;
- контурная ЭДС i –го контура.
Тогда уравнения для независимых контуров согласно II закону Кирхгофа примут вид:
.
Вторая матрица соединений (инциденций) N, или матрица соединений ветвей в независимые контуры.
Она представляет собой таблицу, строки которой отвечают независимым контурам, а столбцы — ребрам (ветвям) направленного графа.
Элементы матрицы N могут принимать одно из 3-х значений:
+1 – если ветвь j входит в контур i, и направление ветви j совпадает с направлением обхода контура i;
nij = -1 – если ветвь j входит в контур i, и направление ветви j не совпадает с направлением обхода контура i;
0 – если ветвь j не входит в контур i.
Для направленного графа Рис.5.1 получаем вторую матрицу соединений в виде
(1.5)
ветви
Совокупность двух матриц инциденций – полное однозначное описание направленного графа схемы, т.е. можно составить направленный граф, имея обе матрицы. Это алгебраическая запись геометрического образа сети.
Для схемы замещения Рис 1.5 найдем произведение второй матрицы соединений N на столбцевую матрицу падений напряжения в сопротивлениях ветвей.
В компактной форме
BZ = E K (1.6)
- первая форма второго закона Кирхгофа в матричном виде.
Падения напряжения в сопротивлениях ветвей зависят от токов и сопротивлений этих ветвей. Аналитически эту зависимость можно записать в матричной форме с помощью матрицы сопротивлений ветвей. Эта матрица имеет квадратную форму, её строки и столбцы отвечают ветвям рассматриваемой схемы. Сопротивления ветвей располагаются по главной диагонали этой матрицы. Если же в схеме имеются ветви, связанные магнитным потоком взаимоиндукции, то матрица сопротивлений ветвей должна содержать сопротивления взаимоиндукции на пересечении строк и столбцов, отвечающих магнитосвязанным ветвям. В нашей схеме взаимоиндукция не учитывается, поэтому получим диагональную матрицу.
ветви
ветви
Произведение матрицы сопротивлений в ветвях на матрицу токов ветвей позволяет получить матрицу падений напряжения в сопротивлениях ветвей.
.
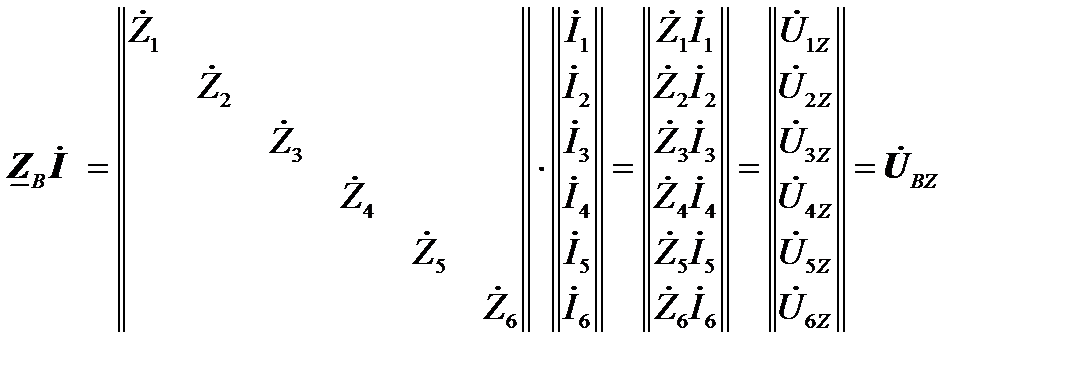В компактной форме:
.
После подстановки этого выражения в (1.6) получаем вторую (основную) форму второго закона Кирхгофа в матричном виде.
. (1.7)
Если найти произведение второй матрицы соединений N на столбцевую матрицу ЭДС ветвей Е, то получим матрицу, в каждой строке которой будет алгебраическая сумма ЭДС, входящих в один независимый контур, аналогично тому, как произведение матриц 
и 
определило матрицу суммы падений напряжения в ветвях этих контуров. Следовательно:
.
После подстановки этого выражения в правую часть (1.7) получаем третью форму второго закона Кирхгофа в матричном виде:
(1.8)
