Ціль роботи: Вивчення методики ідентифікації об’єктів
управління в частотному просторі.
З попередньої роботи видно, що методи ідентифікації в часовому просторі достатньо чутливі до дій неконтрольованих середньо час-тотних збурень, що в свою чергу призводить до помилки в виборі структури математичної моделі об’єкта управління.
Якщо на вхід об’єктів управління подавати ідентифікуючий сигнал
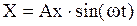
де: Ax – амплітуда, ώ – частота вхідного сигналу.
Через деякий час на виході об’єкта появиться періодичний сигнал
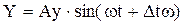
де: Ay – амплітуда сигналу на виході об’єкта, Δt – час на який вихідний сигнал запізнюється відносно вхідного сигналу або опереджає його.
В цьому випадку, якщо під час експерименту на об’єкт діяли неконтрольовані зовнішні збурення то їх вплив проявиться на зміні вихідної координати Y лише в моменти дії збурення, а якщо об’єкт має резонансні властивості то ці властивості проявляться симетрично як на позитивних так періоди експерименту і відкинути ті відрізки де діяли неконтрольовані зовнішні збурення, тобто підвищити чистоту експерименту і запобігти помилці в виборі структури математичної моделі.
В ході експерименту регіструючим приладом одночасно записуються вхідний і вихідний сигнали рис. 5.
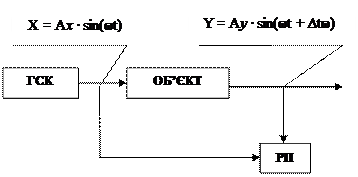
Рисунок 5 – Структурна схема
Величина амплітуди Ay і частоти ώ встановлюються на спеціальному генераторі синусоїдальних коливань ГСК. Вхідний сигнал Х і вихідний сигнал Y записуються на діаграмній стрічці реєструючого приладу РП. Отримавши діаграмний запис сигналів рис. 6 дуже просто можна визначити модуль і фазу об’єкта управління на частоті експерименту.
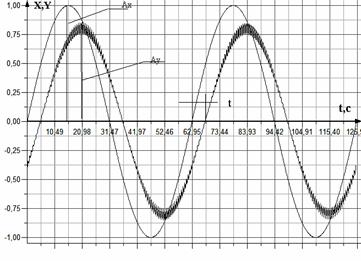
Рисунок 6 – Часова діаграма
 (4)
(4)
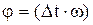 (5)
(5)
Провівши експеримент при декількох значеннях частоти ώ можна також визначити величину модулів і фаз та явної і неявної складових комплексної частотної характеристики (КЧХ) об’єкта управління і побудувати КЧХ в комплексній площині рис. 7.
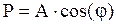 (6)
(6)
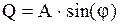 (7)
(7)
де: Р – явна, Q – неявна складові КЧХ
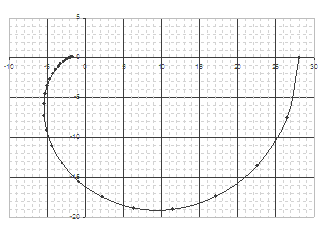
Рисунок 7 – Експериментальна КЧХ об’єкта
Звичайно, що з вигляду КЧХ об’єкта важко вибрати структуру моделі вигляді конкретної передаточної функції. Тому при виборі структури моделі, враховуючи те, що річ йде про конкретні технологічні об’єкти подібні яким вже експлуатуються в промисловості, використовують так звану апріорну (відому раніше) інформацію.
Критерієм адекватності в даному випадку буде точний збіг комплексної частотної характеристики моделі з КЧХ реального об’єкта у всьому діапазоні частот.
Завдання ідентифікації в цьому випадку полягає в знаходженні передаточної функції об’єкта по експериментально отриманні КЧХ об’єкта.
Наприклад, велику кількість об’єктів можна описати передаточною функцією наступного вигляду:
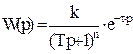 (8)
(8)
Оскільки в процесі експерименту визначалися значення модуля А і фази φ об’єкта то запишемо аналітичні вирази для визначення модуля Ам і фази φм моделі.
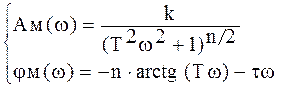 (9)
(9)
Оскільки критерієм адекватності є збіг КЧХ моделі і об’єкта у всьому діапазоні частот, то в систему рівнянь (9) замість Aм(ώ) і φм(ώ) можна підкласти A(ώ) і φ(ώ) об’єкта на відповідній частоті величина яких відома з експерименту
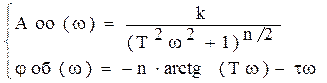 (10)
(10)
Система рівнянь (10) представляє собою систему двох рівнянь з чотирма невідомими К,Т, n, τ.
Якщо задатися спочатку величиною n і τ, то з системи рівнянь (10) можна знайти величину К і Т.
 (11)
(11)
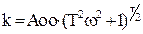
Оскільки КЧХ моделі повинна точно відтворювати КЧХ об’єкта, то необхідно провести перевірку виконання умов:
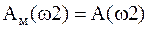 (12)
(12)

Якщо ці умови не виконуються, то в систему рівнянь (9) замість Aм(ώ) і φм(ώ) підкладаються значення A(ώ2) і φ(ώ2) і отримана система розв’язується в цьому випадку вже відносно n і τ.
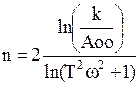 (13)
(13)
 (14)
(14)
Далі знову проводиться перевірка умов на частоті ώ3
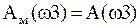
(15)

Якщо ці умови не виконуються, то в систему рівнянь (9) замість Aм(ώ) і φм(ώ) підкладаються значення A(ώ3) і φ(ώ3) і система розв’язується відносно К і Т. Процедура повторяється до тих пір доки не будуть виконанні умови адекватності.
Процедуру ідентифікації можна представити в вигляді блок – схеми рис. 8.
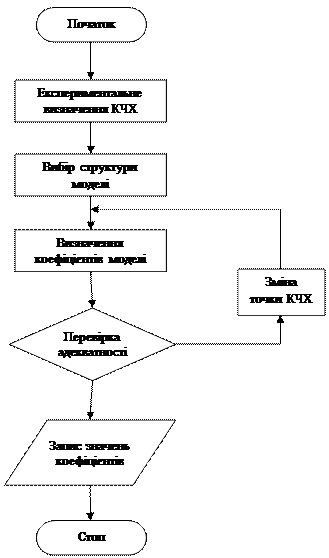

Рисунок 8 – Блок – схема процесу ідентифікації
Завдання на лабораторну роботу
1. Вивчити методику ідентифікації.
2. В залежності від номера варіанту із завдання вибрати оцінки частотної характеристики об’єкта.
3. Вибрати структуру моделі.
4. Визначити величину коефіцієнтів моделі.
5. Перевірити адекватність моделі і об’єкта.
ЛАБОРАТОРНА РОБОТА 3






