Критерий Фишера может быть использован для сравнения точности двух (или нескольких) конкурирующих моделей.
Пусть рассматриваются две модели изучаемой системы (w1, w2), приводящие к двум различным множествам значений функции отклика: Wm 1, Wm 2.
Будем считать, что модель w2 более подробна и предположительно более точна, чем w1. Для каждой из моделей может быть составлена остаточная сумма квадратов:
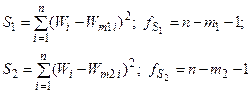
и подсчитаны средние квадраты этих сумм (выборочные дисперсии):

Для сравнения моделей подсчитывается так называемая дополнительная сумма квадратов SS, связанная с дополнительными данными, введенными в модель w2 , и характеризующаяся внесенными в нее уточнениями; а также число степеней свободы этой дополнительной суммы квадратов:
SS = S 1 – S 2; fSS = fS 1 – fS 2 = m 2 – m 1.
Средний квадрат дополнительной суммы определяется соотношением
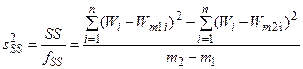 .
.
Если известна дисперсия экспериментальных данных s2(W), то роль дополнительной информации, содержащейся в модели w2, оценивается путем сравнения F -отношения с пороговым (критическим) значением критерия Фишера:
 .
.
Если дисперсия экспериментальных данных s2(W) неизвестна, сравнение проводится с оценкой дисперсии для упрощенной модели 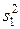 :
:
 .
.
Если полученное значение критерия Фишера значимо:
 или
или 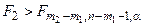 ,
,
то дополнительная информация, заложенная в модели w2, существенна, и модель w2 действительно отличается от модели w1. В противном случае уточнения, вносимые моделью w2, неразличимы на фоне шума; с точки зрения точности модели равноценны, и предпочтение должно быть отдано более простой модели w1.
В частном случае полиномиальных моделей, представляющих собой конечные отрезки бесконечных рядов, этим методом можно проверить целесообразность включения в модель членов рада с более высокими степенями.
Рассмотрим пример, приведенный в п. 3.2 (лекция 7) с построенной моделью в виде полинома второй степени. Проанализируем целесообразность использования для данной выборки кубической модели типа Wm= a 0 + a 1 x + a 2 x 2 + a 3 x 3.
В результате расчетов методом наименьших квадратов можно найти коэффициенты такой модели:
Wm = –0,878 + 4,98 x – 0,768 x 2 + 0,032 x 3.
Вычислим остаточную сумму квадратов:
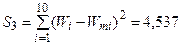 .
.
Напомним, что остаточная сумма квадратов для модели второго порядка имела значение S 2 = 4,393.
Дополнительная сумма квадратов
SS = S 2 – S 3 = 0,144; fSS = m 3 – m 2 = 4 – 3 = 1.
Средний квадрат дополнительной суммы
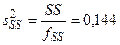 .
.
Критерий Фишера
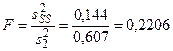 .
.
По статистическим таблицам распределения определяем критическое (пороговое) значение критерия Фишера при количестве степеней свободы f = n – m 2 – 1 = 10 – 3 – 1 = 6 и уровне риска a = 0,05
 .
.
В связи с тем, что полученное из расчета значение критерия Фишера меньше критического, можно считать, что член третьего порядка не добавляет существенной информации и, следовательно, он является незначимым. Переход к модели третьего порядка нецелесообразен.
Контрольные вопросы к лекции 10
1. Обеспечивает ли получение бóльшей точности более сложная модель?
2. Перечислите методы выбора оптимальной модели.
3. На чем основан метод всех возможных регрессий?
4. На чем основан метод исключения?
5. На чем основан метод включений?
6. На чем основан подход регуляризации?
7. Опишите критерий проверки значимости высших степеней математической модели.
Глава 4. Математические модели
Лекция 11
теории принятия решений






