Доведення властивостей 1) — 5).

Доведемо спочатку властивість 1). Маємо Mb ₁= 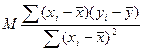. При цьому 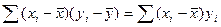(Переконайтеся у вірності останньої рівності). Враховуючи ще рівність

y_i = β ₀ + β ₁ x_i + ε_і, (4.11)

одержуємо

Mb ₁ = =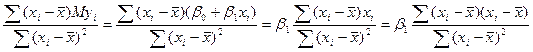

= .

Mb ₀ = .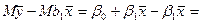

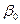Рівності (4.6) доведено.

Аналогічним чином отримуємо:

Db ₁= .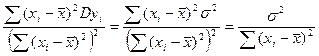

Другу з нерівностей (4.7) доведено. Першу з зазначених нерівностей буде доведено трохи пізніше. Перед доказом властивості 3) нагадаємо, що для випадкових величин x, h їх коваріація Cov (x, h) обчислюється за формулою Cov (x, h) = Мxh – Мx Мh. Згадаємо також кілька властивостей коваріацій випадкових величин та коваріаційних матриць випадкових векторів.

1. Для випадкової величини x має місце рівність Cov (x, x) = Dx.

2. Для випадкових величин x, h, x ₁, x ₂, h ₁, h ₂ та сталих а ₁, а ₂ мають місце рівності

Cov (а ₁ x ₁+ а ₂ x ₂, h) = а ₁ Cov (x ₁, h) + а ₂ Cov (x ₂, h),

Cov (x, а ₁ h ₁ + а ₂ h ₂) = а ₁ Cov (x, h ₁) + а ₂ Cov (x, h ₂).

3. Нехай D (x, h) – коваріаційна матриця випадкових векторів x, h, що мають компоненти x ₁, x ₂,… та h ₁, h ₂,… відповідно (так що на місті (i, j) матриці D (x, h) стоїть величина Cov(x_i, h_j)); нехай також А, В – невипадкові матриці. Тоді D (Аx, Вh) = АD (x, h) 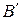, де 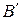– транспонована до В матриця.

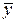Повернемося до доказу властивості 3) оцінок МНК. Нехай Y = (y ₁, y ₂,..., y_n)' – n -вимірний вектор-стовбець спостережень, А = , В = . Легко бачити, що = АY, b ₁ = ВY. При цьому DY = σ ² I, де I – одинична матриця розміру n ´ n. Отже, використовуючи властивість 3. коваріаційної матриці, одержуємо

Cov (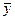, b ₁) = Cov (АY, ВY) = А (DY) В ' = 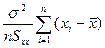= 0,

тобто рівність (4.8) доведено. Тепер, користуючись відомою властивістю дисперсії суми некорельованих випадкових величин, одержимо:

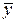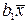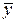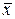Db ₀ = D ( – ) = D + ² D = =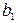

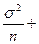
= , що й доводить першу з нерівностей (4.7). Для доказу (4.9), використовуючи відомі властивості коваріацій випадкових величин, знайдемо:

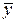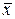Cov (b ₀, b ₁) = Cov ( – b ₁ , b ₁) = Cov (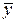, b ₁) + Cov (– b ₁ 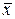, b ₁) = – 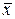Cov (b ₁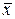, b ₁) = = – Db ₁.

Тепер лишається скористатися другою з властивостей 2).

Нарешті, згідно з рівностями (2.10) та (4.8), маємо

D ŷ ₀ = D [ 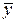+ (х ₀ – х) b ₁] = D 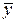+ (х ₀ – х)² D b ₁.

Тепер лишається скористатися рівностями (4.5) та (4.7). Зауважимо, що дисперсія величини ŷ ₀ є мінімальною, коли точка х ₀ співпадає з 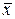і зростає при віддаленні цієї точки від .

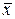4.2. Нормальність випадкової складової. Надалі постійно припускатиметься, що випадкова складова e регресійної моделі (2.3) є нормально розподіленою випадковою величиною з нульовим математичним сподіванням і деякою (невідомою) дисперсією s ²:

e Î N (0, s). (4.12)

Припущення, зроблені вище, зумовлюють, що вектор випадкових складових E = (e ₁, e ₂,…, e_п), де e_i = y_i – (β ₀ + β ₁ x_i), i = 1,2,…, n, є нормально розподіленим випадковим вектором з взаємно незалежними компонентами, кожна з яких має тип (4.12). Зокрема, коваріаційна матриця D (E) вектора E є діагональною з елементами s ² на головній діагоналі:

D (E) = = s ² I_n, (4.13)

де I_n – одинична матриця розміру n ´ n.

Позначимо ще Y вектор спостережень, тобто Y = (y ₁,…, y_n). Зауважимо, що оскільки β ₀ + β ₁ x_i — є невипадковими величинами, то

D (Y) = D (E). (4.14)

З припущення (4.12) випливає дуже багато корисних наслідків. Зокрема, такими є дві наступні теореми, справедливість яких буде наведено у подальших розділах курсу як наслідок деяких більш загальних положень.

4.2.1. Теорема. Остаточна сума квадратів, поділена на s ², має розподіл c² з

n – 2 степенями волі, коротше:

RSS / s ² Îc² _{n –2},

де RSS = S(y_i – ŷ_i)².

4.2.2. Зауваження. Нехай відомо, що відношення деякої випадкової величини 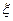до деякої сталої величини (параметру) q має розподіл c² з m степенями волі. Тоді відношення 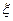/ m є незсуненою оцінкою для q.

ð Дійсно, оскільки x / q має розподіл c² _m, то M (x / q) = m, тому M (x / m) = q. ð

Позначимо

RSS /(n – 2) = S ². (4.15)

4.2.3. Наслідок. Величина S ² є незсуненою оцінкою величини s ²:

M S ² = s ² (4.16)

4.2.4. Зауваження. Можна довести, що рівність (4.16) є справедливою і без припущення щодо нормальності розподілу x (за виконанням інших зроблених вище припущень щодо випадкової складової моделі (2.3).

4.2.5. Наслідок. Величини

b ₀ = S ², b ₁ = 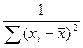S ² (4.17)

є незсуненими оцінками величин Db ₀ та Db ₁ відповідно.

4.2.6. Теорема. За умови (4.12) мають місце співвідношення

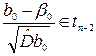, (4.18)

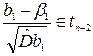, (4.19)

де t_{n – 2} — розподіл Стьюдента з n – 2 степенями волі.

4.2.7. Наслідок. Нехай 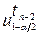– квантиль рівня 1 – α /2 розподілу Стьюдента

t_{n –2}. Тоді інтервали

B ₀ = [(b ₀ – ],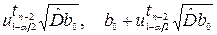

B ₁ = [(b ₁ – ],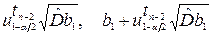

є довірчими інтервалами рівня α для параметрів b ₀ та b ₁ відповідно.

ð Це випливає із співвідношень (4.18), (4.19) та тією властивістю квантилів неперервних випадкових величин, що F (u_p) = p, де F – функція розподілу даної випадкової величини, u_p – її квантиль рівня p. ð

4.2.8. Зауваження про перевірку гіпотез щодо значень коефіцієнтів β ₀, β ₁.

Щойно наведені результати дають змогу перевіряти гіпотези 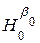: β ₀ = b ₀⁰ та : β ₁ = b ₁⁰, де b ₀⁰ та b ₁⁰ – фіксовані числа. Ідея перевірки є дуже простою. Якщо число b ₀⁰ належить інтервалові B ₀, то гіпотеза 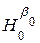приймається, у протилежному випадку – не приймається. Аналогічно перевіряється гіпотеза .

Досить часто, зокрема, в комп’ютерних реалізаціях даної процедури перевірки використовуються дещо інші (формально, але не по суті) дії. А саме, позначимо T (b ₀) (T (b ₁)) величину з правої частини (4.18) ((4.19)) при β ₀ = b ₀⁰ (β ₁ = b ₁⁰). Ця величина порівнюється з 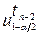– квантилем рівня 1 – α /2 розподілу Стьюдента t_{n –2}. Відповідна гіпотеза не приймається, якщо за абсолютною величиною вказана величина перевищує даний квантиль. Іншими словами, гіпотеза не приймається, якщо T (b ₀) (відповідно, T (b ₁)) попадає у двосторонню критичну множину (– ¥, – 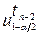) È (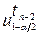, + ¥). За наявністю альтернативної гіпотези { b_i ³ b_i ⁰} ({ b_i £ b_i ⁰}), i Î {0,1}, доцільніше використовувати односторонню критичну множину (, + ¥) ((– ¥, – )

Особливо часто доводиться перевіряти гіпотезу при b ₁⁰ = 0 (тобто мова йде про перевірку гіпотези { β ₁ = 0}. У цьому випадку називається гіпотезою про незначимість коефіцієнту регресії. Якщо вона приймається, то можна вважати, що y не залежить від x (в рамках лінійної моделі(2.3)).

4.2.9. Зауваження. Деякі поширені комп’ютерні статистичні програми, наприклад, Statgraphics 3.0, використовують дещо іншу техніку перевірки гіпотез. А саме, не фіксуються заздалегідь критичні множини, а обчислюються так звані P -значення (P -values). Зокрема, при перевірці гіпотези 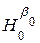() P -значення є ймовірністю того, що за умови справедливості даної гіпотези, статистика T (b ₀) (відповідно, T (b ₁)) буде за абсолютною величиною рівною або більшою того значення, що конкретно отримано. Малість P -значення свідчить про недоцільність довіри до цієї гіпотези. Навпаки, великі P -значення свідчать на користь гіпотез, що перевіряються. Так, малі P -значення при перевірці гіпотези з b ₁⁰ = 0 свідчать про значимість коефіцієнту регресії b ₁. З коментарів, які містяться у відповідних роздруківках, можна зрозуміти, що вважається малим, а що – великим P -значенням у кожному конкретному випадку.