Для розв’язання задачі (2.4) обчислимо частинні похідні по b 0, b 1 функції S = S (b 0, b 1). Маємо
¶ S / ¶ b 0 = - 2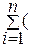 
yi – b 0 – b 1 xi),
¶ S / ¶ b 1 = - 2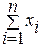 
(yi – b 0 – b 1 xi).
Прирівнюючи знайдені похідні нулю і виконуючи належні спрощення (рекомендується виконати їх самостійно), приходимо до системи двох рівнянь, в якій, підкреслимо, невідомими є параметри b 0, b 1:
b 0 n + b 1 S xi = S yi,
b 0 S xi + b 1 S xi 2 = S xi yi, (2.5)
де для спрощення запису індекси підсумовування опущено. Ця система носить назву системи нормальних рівнянь або нормальної системи. В одному з наступних розділів буде доведено, що розв’язок нормальної системи і справді є розв’язком задачі (2.4).
Розглянемо спочатку випадок існування та єдиності розв’язку системи (2.5). Тобто ми поки що вважаємо визначник даної системи відмінним від 0. Позначимо шуканий розв’язок (b 0, b 1); відносно b 1 маємо (переконайтесь у цьому):
, (2.6)
де підсумовування ведеться по i від 1 до n. Розв’язок нормальної системи відносно b 0 має такий вигляд:
b 0 =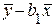 
, (2.7)
де 
та 
– відповідні середні арифметичні значення:
= (y 1+…+ yn)/ n, = (x 1+…+ xn)/ n.
2.3.1. Зауваження. Оцінка b 1 параметра b 1 може бути записаною також іншим чином:
. (2.8)
Дійсно, це твердження випливає з наступних рівностей
S(xi – )(yi – ) = S xi yi – S yi – S xi + n = S xi yi – n =
= S xi yi – (S xi)(S yi)/ n.
Зручно ввести позначення:
Sx y = S(xi – )(yi – ), Sx x = S(xi – )2, Sy y = S(yi – )2.
Тоді маємо легкий для запам’ятовування вираз оцінки b 1:
b 1 = Sx y / Sx x . (2.9)
Вище була введена функція
= 
= b 0 + b 1 x (2.10)
Величина = є оцінкою функції регресії g (x) з рівності (2.2). Іноді зручніше використовувати дещо інший вираз для :
= + b 1(x – ). (2.11)
Ця рівність одержується з (2.10) підстановкою замість b 0 його виразу (2.7).
З рівності (2.11) одразу бачимо, що пряма лінія, яка зображує у декартовій площині залежність = , проходить через точку декартової площини з координатами (, ).
Припустимо тепер, що визначник D системи (2.5) дорівнює 0. З’ясуємо, за яких умов це трапляється. Маємо
D = n S xi 2 –(S xi)2.
Оскільки (S xi)2 = (S 1× xi)2, то за нерівністю Коші – Буняковського буде (S xi)2 
S 12 × S xi 2 = n S xi 2, отже завжди
D ³ 0 (2.12)
Скористаємось відомою умовою наявності рівності в нерівності Коші – Буняковського. Бачимо, що коли ввести n -вимірні вектори 1 = (1,…,1) і x = (x 1,…, xn), то рівність в (2.12) буде мати місце тоді і тільки тоді, коли вектори 1 і x будуть лінійно залежними. Це означає, що знайдуться такі сталі с 1, с 2, що одночасно не дорівнюють 0 і для яких виконується рівність
с 1 × 1 + с 2 × x = 0, (2.13)
де права частина – це нульовий вектор (0,…,0). При цьому випадок с 2 = 0, очевидно, не може мати місця (бо інакше, оскільки тоді с 1 
0, буде 1 = 0). Тому з (2.13) випливає, що x = (с,…, с), де с – деяка стала. Це означає, що всі спостереження робляться в одній точці: x 1 = … = xn = с. За вказаною умовою система (2.5) зводиться, фактично, до одного-єдиного рівняння
b 0 n + b 1 nс = S yi, (2.14)
яке має безліч дійсних розв’язків.
2.3.2. Висновок. З розглянутого вище бачимо, зокрема, що нормальна система рівнянь (2.5) завжди сумісна, незалежно від того, дорівнює її детермінант 0 чи не дорівнює. В останньому випадку маємо єдиний розв’язок, що дається рівностями (2.6) ((2.8)) і (2.7). Перший випадок може трапитись тільки тоді, коли всі спостереження проводяться лише при одному значенні x. У цьому випадку вказана система має безліч розв’язків, кожен з яких може бути знайдений з рівняння (2.14).
РОЗДІЛ 3
