Вектор залишків простої лінійної регресії та деякі його властивості.

Визначимо так звані залишки регресійної моделі (2.3). За означенням, це величини e_i = y_i – , де , i = 1,…, n. Вектором залишків моделі (2.3) називається вектор e = (e ₁,…, e_n). Зауважимо, що коли з самого початку вільний член b ₀ входив у модель (тобто не покладався одразу рівним 0), то сума всіх залишків (інакше, сума координат вектору залишків) дорівнює 0, тобто

å е_i = 0 (3.1)

Це одразу випливає з рівності ¶ S /¶ b ₀ = 0 при b ₀ = b ₀, b ₁ = b ₁ (див. рівність на с. 9). Зазначена властивість використовується, наприклад, при перевірці обчислень за МНК, якщо останні виконувалися вручну.

3.1. Зауваження. Корисно помітити, що середнє арифметичне значень , i = 1, 2, …, n дорівнює – середньому значенню спостережуваних відгуків y ₁,…, y_n. Тобто, коли позначити

= , i = 1, 2, …, n; =( +…+ )/ n,

то матимемо рівність

= . (3.2)

Дійсно, згідно з рівністю (2.10) маємо

= / n = ( ( + b ₁(x_i – )))/ n = + b ₁ – b ₁ = .

З рівності (3.2) одразу випливає вже відзначений вище факт рівності 0 суми координат вектора залишків e:

S e_i = S (y_i – ) = n – n = 0.

(Нагадаємо, що коли не робиться спеціальних роз’яснень, то за відсутністю індексів у символі S мається на увазі підсумовування від 1 до n).

3.2. Про одну властивість оцінок МНК.

У багатьох питаннях регресійного аналізу є корисною наступна рівність

S(y_i – )² = S(y_i – )² + S( – )². (3.3)

Дана рівність часто називається основною тотожністю дисперсійного аналізу. (Зміст цієї назви стане зрозумілим дещо пізніше.) Сама ж рівність (3.3) може бути одержана наступним чином.

S(y_i – )² = S(y_i – + – )² = S(y_i – )² + S( – )² +

+ 2S( – ) ( – ).

Тепер досить довести, що остання сума дорівнює 0. Використовуючи рівність (2.10), маємо

– = b ₁(x_i – ), y_i – = y_i – – b ₁(x_i – ).

Звідси вказана сума дорівнює

S b ₁(x_i – )((y_i – ) – b ₁(x_i – )) = b ₁(S_{x y} – b ₁ S_{x x}) = 0

(врахувати рівність (2.9)). Рівність (3.3) доведено.

З аналогічних міркувань також зрозуміло, що

S( – )² = S(b ₁(x_i – ))² = b ₁² S_{x x} = b ₁ S_{x y}. (3.4)

Зауважимо, що суми квадратів у рівності (3.3) мають спеціальні назви. Сума зліва – сума квадратів відносно середнього; перша сума справа – сума квадратів відносно регресії; друга сума справа – сума квадратів, що зумовлена регресією.

3.3. Пояснювана частина варіації даних.

Позначимо

R ² = . (3.5)

З рівності (3.3) одразу випливає нерівність

R ² £ 1. (3.6)

Можна вважати, що величина R ² вимірює „долю загального розкидання даних, що пояснюється регресією”. Її часто вимірюють в процентах, помножуючи на 100. Досить часто величина R ² носить назву „ коефіцієнт детермінації ”. Величина R ² виводиться на друк у більшості відомих комп’ютерних програм з регресійного аналізу. Чим ближчою є величина R ² до 1, тим краще функція регресії (2.9) відповідає дійсному характеру зв’язку між незалежною та залежною змінними.

3.2.1. Зв’язок величини R ² з вибірковими коефіцієнтами кореляції R _{x y} та .

Як відомо, коефіцієнтом кореляції між випадковими величинами x, h називається вираз

r_xh = Cov(x, h) / (Dx × Dh)^{1 / 2},

де Cov(x, h) = Мxh – Мx Мh, D – символ дисперсії.

Оцінкою коефіцієнта кореляції (або вибірковим коефіцієнтом кореляції) між двома величинами x та h є вираз

R_xh = , (3.7)

де (x_i, h_i), i = 1,..., n – значення (x, h) в n незалежних експериментах, та – відповідні середні арифметичні, а підсумовування виконується від 1 до n.

Позначимо R_xy та , відповідно, вибіркові коефіцієнти кореляції між x та y і y та ŷ відповідно. Тоді мають місце рівності

= sign (b ₁) × R_xy (3.8)

де

sign x =

R ² = (R_xy)², (3.9)

R ² = ()² (3.10)

Дійсно, з використанням (3.4) одержуємо

= sign (b ₁)× R_xy (3.11)

З іншого боку,

R ² = = (R_xy)².

(3.11) і останні співвідношення доводять рівності (3.8) — (3.10).

РОЗДІЛ 4.

Ймовірнісні припущення про випадкову складову моделі простої лінійної регресії та їх наслідки.

4.1. Незалежність, однорідність і відсутність систематичних похибок.

Надалі буде вважатися, що всі експерименти є незалежними, виконуються в однакових умовах і не мають систематичних похибок. Математично це виражається наступним чином. Нехай ε_і позначає величину похибки в і -му експерименті (тобто ε_і = y_i – (β ₀ + β ₁ x_i)), і = 1,..., n Тоді вектор похибок ε = (ε ₁,..., ε_n) становить собою сукупність незалежних однаково розподілених випадкових величин, причому математичні сподівання кожної з цих величин дорівнюють 0:

Mε_і = 0, і = 1,..., n, (4.1)

а дисперсії дорівнюють деякій сталій σ²:

Dε_і = σ ², і = 1,..., n. (4.2)

4.1.1. Зауваження. З (4.1) та (4.2) одразу випливають рівності (переконайтеся в цьому):

Mу (х) = β ₀ + β ₁ х, (4.3)

D у (х) = σ ², (4.4)

D 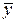= σ ² ∕ n (4.5)

4.1.2. Наслідки. Наслідками зроблених вище припущень є також наступні властивості оцінок параметрів моделі:

1) Mb ₀ = β ₀, Mb ₁ = β ₁; (4.6)

2) Db ₀ = σ ², Db ₁ = 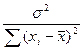. (4.7)

3) Cov (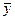, b ₁) = 0, (4.8)

4) Cov (b ₀, b ₁) = . (4.9)

5) Нехай х ₀ – довільне значення змінної х. Позначимо ŷ ₀ значення оцінки функції регресії ŷ в точці х ₀. Тоді має місце рівність

D ŷ ₀ = . (4.10)

Зокрема, рівності (4.6) означають, що b ₀ та b ₁ є незсуненими оцінками, відповідно, величин β₀ та β₁. Рівності (4.7) дають вирази дисперсій оцінок коефіцієнтів регресії через дисперсію випадкової складової моделі (2.3). Рівність (4.8) стверджує некорельованість величин 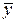та b ₁. Рівність (4.9) дає явний вираз коваріацій між оцінками b ₀, b ₁, а (4.10) — вираз дисперсії оцінки функції регресії у довільній точці спостережень. З останньої рівності одразу бачимо, що дисперсія величини ŷ ₀ є мінімальною, коли точка х ₀ співпадає з 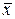і зростає при віддаленні цієї точки від .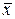