Мы можем получать вывод из посылок путем преобразования последних. Истинность вывода в этом случае целиком зависит от истинности посылок, если, разумеется, не нарушены правила преобразования, которые, в свою очередь, обусловлены формой посылок.
В суждении, которое составляет содержание посылки, мы утверждаем или отрицаем какое-либо из взаимосвязанных отношений, непосредственные умозаключения позволяют выявить другие стороны суждений. С их помощью мы выявляем то, что не было явно выражено и тем самым уточняем наше знание, заключенное в посылке.
К основным формам непосредственных умозаключений относятся: превращение суждений, обращение суждений и противопоставление предикату. Вы уже выполняли логические операции с преобразованием суждений. Эти же операции являются и простыми умозаключениями. Надеюсь, что этот параграф более уточнит ваши знания о суждениях и умозаключениях.
1. Превращение суждений (лат. – obversio) – это непосредственное заключение о том, как относится к субъекту данной посылки понятие, противоречащее её предикату.
Превращение суждений представляет собой преобразование одного суждения. Оно состоит в том, что из данного суждения получаем новое, противоположное ему по качеству. Рассмотрим суждения: «Иванов не является плохим студентом» и «Иванов – неплохой студент». Во втором суждении отрицание передвинули со связки на предикат и получили новое суждение, которое по своему содержанию хоть и незначительно, но отличается от исходного – усилилась похвала Иванову. Мы отрицательную связку заменили на положительную (изменилось качество суждения) и предикат «плохой студент» заменили на предикат «неплохой студент».
Смысл превращения состоит в том, что мы выявляем в утвердительном суждении отношение различия, а в отрицательном – отношение тождества, содержащиеся в суждениях в неявной форме.
Формально операция превращения состоит в том, что мы изменяем связку исходного суждения на противоположную и заменяем его предикат противоречащим понятием. Например:
Все металлы – химические элементы(Ѕ есть Р)
Ни один металл не есть не химический элемент (Ѕ не есть не Р).
Поскольку изменяется качество суждения, то превращение возможно из общеутвердительного в общеотрицательное и наоборот, из частноутвердительного в частноотрицательное, и наоборот:
1. Все Ѕ есть Р " Ни одно Ѕ не есть не Р
2. Ни одно Ѕ не есть не Р " Все Ѕ есть Р
3. Некоторые Ѕ есть Р " Некоторые Ѕ не есть не Р
4. Некоторые Ѕ не есть Р " Некоторые Ѕ есть не Р
Единственная ошибка, которая может быть при превращении, это подмена понятия, противоречащего предикату посылки, каким-нибудь похожим на противоречащее, либо противоположным предикату, или состоящим вместе с предикатом из ограничения одного и того же понятия двумя противоречащими. Например: зависть не есть белый предмет; следовательно, она есть небелый предмет.
2. Обращение суждений (лат. – conversio)
Обращение есть непосредственное суждение о предикате данного суждения.
Обращение суждений определяется тем обстоятельством, что мы получаем новое знание не только о предмете, мыслимым в субъекте, но и о предметах, мыслимых в предикате. Для этого мы в выводе меняем местами субъект и предикат и получаем новое суждение, в котором субъектом становится предикат исходного суждения, а предикатом – субъект исходного суждения. При этом качество суждения не меняется.
Все правила обращения легко найти, если, взяв какое-нибудь суждение, менять его качество и количество (при этом получится четыре формы этого суждения: 1) все Ѕ есть Р, 2) некоторые Ѕ есть Р, 3) ни одно Ѕ не есть Р, 4) некоторые Ѕ не есть Р и пробовать, можно ли при данной форме суждения сделать из него одного правильный вывод о его предикате. После этих проб можно убедиться, что обращение подчиняется двум правилам: 1) из частноотрицательной посылки нельзя сделать никакого вывода; 2) при обращении правильный вывод получается только из общеотрицательной посылки. Во всех остальных случаях правильный вывод может быть только частным.
Обращение подчиняется следующему правилу: термин, не распределенный в исходном суждении, не может быть распределен в новом, выводном суждении.
Обращения делятся на простые и с ограничением. В простом обращении количество суждений не меняется. Это бывает в том случае, когда оба термина исходного суждения либо распределены, либо не распределены.
В обращении с ограничением либо субъект, либо предикат исходного суждения не распределены. Если предикат исходного суждения не распределен, то он, став субъектом выводного суждения, остается не распределенным.
Схема обращения: Ѕ есть Р
Р есть Ѕ.
Общеутвердительное суждение обращается в частноутвердительное, общеотрицательное – в общеотрицательное, частноутвердительное – в частноутвердительное, частноотрицательное на практике не обращается.
Ошибки при обращении называются неправильным обращением. Они появляются при нарушении одного из указанных правил. Например: металлы не всегда бывают жидкостями, потому что некоторые жидкости вовсе не металлы (вывод из частноотрицательной посылки), или: разумные животные только люди, потому что всякий человек разумное животное (общий вывод из общеутвердительной посылки).
Для того, чтобы наиболее эффективно производить непосредственные умозаключения, необходимо видеть, распределен или не распределен субъект и предикат исходного суждения (см. таблицу распределенности терминов в суждении).
3. Противопоставление предикату (лат. – opposition praedicati) ‑ это умозаключение, состоящее из соединения превращения с обращением.
Противопоставлением предикату называется вывод нового суждения, субъектом которого является понятие, противоречащее предикату исходного суждения. А предикатом – субъект исходного суждения.
Противопоставление предикату подчиняется двум правилам: 1)из частноутвердительной посылки нельзя сделать правильного заключения путем противопоставления предикату, поскольку эта посылка превращается в частноотрицательное суждение, а обращение из частноотрицательного суждения является неправильным; 2) правильный общий вывод в противопоставлении предикату получается только из общеутвердительного суждения, поскольку общеутвердительное суждение превращается в общеотрицательное, а из последнего через обращение получается правильный общий вывод.
Если исходное суждение является общеутвердительным, то в новом суждении мы получим общеотрицательное суждение.
Если исходное суждение является отрицательным, то в новом суждении мы получим утвердительное суждение. При этом из общеотрицательного суждения получается частноутвердительное выделяющее суждение. Из частноотрицательного суждения выводится частноутвердительное суждение.
Противопоставление предикату можно получить, применяя последовательно операции сначала превращения, а затем обращения. Например, превращаем суждение «все металлы электропроводны», получаем суждение «ни один металл не есть неэлектропроводен». Обращая это суждение, получаем суждение «ни одно неэлектропроводное тело не есть металл».
Теперь отвлекитесь от чтения и попробуйте разобраться самостоятельно в ошибочном выводе из следующего умозаключения: «некоторые гениальные люди не принесли обществу никакой пользы; следовательно, между вредными для общества людьми оказывались иногда гениальные личности».
Применяя логические операции в непосредственных умозаключениях, мы уточняем наши знания, придаем им бóльшую определенность. С помощью этих умозаключений мы выявляем то, что уже содержалось в исходном суждении, но не было явно выражено, делаем неявное явным, неосознанное осознанным.
Силлогизм
Силлогизм (греч. syllogismos – сосчитывание) – это вид умозаключения, в котором требуется определить, следует ли из двух или нескольких суждений данный вывод. Признав истинность посылок мы вынуждены признать истинность заключения.
Если в силлогизме к согласию с выводом нас принуждают только две посылки, то он называется простым силлогизмом, а если посылок больше двух, то он называется сложным.
Простые силлогизмы, в свою очередь, могут быть трех видов:
1) категорические (от греч. kategorikos – утверждающий, решительный, безусловный), в котором обе посылки представлены категорическими суждениями. Например: карась есть рыба (Ѕ есть M), а всякая рыба дышит жабрами (M есть P), следовательно, карась дышит жабрами (Ѕ есть P);
2) разделительные, в которых одна из посылок представлена разделительным (дизъюнктивным) суждением, а другая может быть любой (категорической, условной, разделительной). Например: А есть или В, или С; но А не есть В; следовательно, А есть С;
3) условные, в которых одна из посылок условное суждение, а другая – либо условное, либо категорическое. Например: если А есть В, то С есть D; но А есть В; следовательно, и С есть D.
Обычно категорический силлогизм состоит из двух суждений, которые называются посылками, и третьего суждения, которое называется заключением. Задача заключается в том, чтобы определить, является ли заключение логическим следствием посылок.
В категорических силлогизмах в посылках и заключении присутствуют кванторные слова (все, некоторые, ни один), указывающие на количество суждений, и связки (есть ∕ не есть), указывающие на качество суждений.
Легко убедиться, что в простом категорическом силлогизме должны быть такие понятия, которые есть в посылках, причем одно из понятий, входящих в состав посылок, является общим для обеих посылок. Это, связывающее обе посылки понятие, называется средним термином силлогизма и обозначается символом М (от слова medius – средний).
Оставшиеся в обеих посылках понятия называются крайними терминами силлогизма и различаются по тому, какое место они занимают в заключении: если на месте предиката, то это понятие называется бόльшим термином силлогизма и обозначается символом Р, а если на месте субъекта, - то меньшим термином силлогизма и обозначается символом Ѕ. Посылка, содержащая бόльший термин, называется бόльшая посылка, а содержащая меньший термин – меньшей посылкой.
Посылки могут располагаться в любом порядке, но логическая связь заключения с посылками зависит только от того, какими окажутся по своему составу и форме само заключение и посылки, из которых оно следует. Традиционно большая посылка записывается первой, меньшая – второй.
Посылки и заключение силлогизма классифицируются по наклонениям (moods), сочетающих утверждение (есть) и отрицание (не есть) с кванторными словами (все, некоторые, ни один). Существуют четыре вида наклонений:
| Наклонение | Конкретный пример | Логическая схема | Формула | |
| Общеутвердительное | Все студенты - умные | Все А есть В | ∀A ‑ B | SḁΡ |
| Частноутвердительное | Некоторые студенты - самостоятельные | Некоторые А есть В | ∃A ‑ B | SiΡ |
| Общеотрицательное | Ни один студент не хочет быть отчисленным | Ни одно А не есть В | ∀Ā ‑ ~B | SeΡ |
| Частноотрицательное | Некоторые студенты не умеют плавать | Некоторые А не есть В | ∃A ‑ ~B | SoΡ |
Как мы видим, суждение является общим, если оно содержит кванторные слова «все» или «ни один» (квантор ∀), частным – если содержит кванторное слово «некоторые» (квантор ∃, отрицательным – если содержит отрицание «не», (символ ~ или ¯) и утвердительным, если оно не является отрицательным. Вы можете легко определить суждение, если найдете в нем ключевые термины.
Средний термин в посылках может занимать место либо субъекта, либо предиката. Очевидно, что могут быть четыре позиции, которые занимает средний термин. Мысленно проведите линии, соединяющие три термина силлогизма в этих четырех позициях среднего термина, и вы получите четыре геометрические фигуры. В логике они получили название «фигур силлогизма».
В первой фигуре средний термин (М) занимает место субъекта в большей посылке и место предиката в меньшей посылке.
Во второй фигуре средний термин занимает место предиката в обеих посылках.
В третьей фигуре средний термин занимает место субъекта в обеих посылках.
В четвертой фигуре занимает место предиката в большей посылке и место субъекта в меньшей посылке.
На рисунке это выглядит так:
M P P M M P P M
 |  |  |  | ||||||
 | |||||||||
 |
S M S M M S M S

 1-я фигура 2-я фигура 3-я фигура 4-я фигура
1-я фигура 2-я фигура 3-я фигура 4-я фигура
Отличия силлогизмов одной и той же фигуры, зависящие от количества и качества посылок, называются модусами категорических силлогизмов. Легко увидеть по наклонениям, что в каждой фигуре 16 модусов. Действительно, каждая бόльшая посылка может существовать в четырех формах: общеутвердительная, общеотрицательная, частноутвердительная, частноотрицательная. Такие же формы принимает каждая меньшая посылка, а во всех четырех фигурах – 64 модуса. Если считать единичные посылки, то в четырех фигурах могут существовать 256 модусов. Но при всем таком многообразии лишь 19 модусов дают правильный выбор, при соблюдении законов логики и, не нарушая правил силлогизма – правил фигур, правил терминов и правил посылок.
Правила категорического силлогизма делятся на две группы: А) очевидные и Б) доказательные, зависимые от особенностей каждой фигуры.
Группа А:
1. Терминов должно быть не более и не менее трех (средний, бόльший, меньший).
2. Средний термин должен быть распределен хотя бы в одной из посылок.
3. Термин не может быть распределен в заключении, если он не распределен в посылках.
4. Любой термин, который распределен в заключении, должен быть распределен хотя бы в одной из посылок.
5. Хотя бы одна из посылок должна быть утвердительной.
6. Из двух отрицательных посылок нельзя сделать определенный вывод.
7. Из двух частных посылок нельзя сделать определенный вывод.
8. Если одна из посылок частная, то и заключение должно быть частным.
9. Отрицательный вывод может быть правильным при одной отрицательной посылке.
Группа Б:
1.В первой фигуре бόльшая посылка общая, меньшая – утвердительная.
2.Во второй фигуре бόльшая посылка общая, одна из посылок – отрицательная, вывод только отрицательный.
3.В третьей фигуре меньшая – утвердительная, вывод только частный.
4. В четвертой фигуре при большей утвердительной – меньшая – общая; при какой-либо отрицательной – большая – общая.
Мы уже говорили о том, что логический квадрат позволяет количественные и качественные характеристики суждений выразить буквами А, Е, I, О. В фигурах и правильных модусах они занимают следующее положение:
1-я фигура ‑ А А А, Е А Е, А I I, Е I О;
2-я фигура – Е А Е, А Е Е, Е I O, А О О;
3-я фигура – А А I, I A I, A I I, E A O, O A O, E I O;
4-я фигура ‑ A A I, A E E, I A I, E A O, E I O.
Первые два символа – посылки (бόльшая и меньшая), третий символ – заключение. Попробуем проверить, действительно ли эти 19 модусов являются правильными. Для примера возьмем первый модус первой фигуры. В нем большей посылкой должно быть суждение: «всякое М есть Р», а меньшей посылкой – суждение: «всякое Ѕ есть М». Соблюдая правила силлогизма, мы приходим к общеутвердительному выводу (Все студенты – умные; все учащиеся в УГТУ – студенты, следовательно, все учащиеся в УГТУ – умные).
При построении вывода средний термин не входит в заключение, и оно формируется из крайних терминов. При этом меньший термин становится субъектом заключения, а больший термин – предикатом заключения. Попробуйте изменить в выводе количество или качество суждения и вы придете к неправильному заключению.
Правильность силлогизмов можно проверить с помощью кругов Эйлера. Давайте нарисуем круговые диаграммы, отражающие связи между терминами следующего силлогизма:
 |
 Посылка 1. Всем автовладельцам необходима медицинская страховка.
Посылка 1. Всем автовладельцам необходима медицинская страховка.
 |
Посылка 2. Все депутаты – автовладельцы.
 |
Заключение: всем депутатам необходима медицинская страховка.
Формула построения силлогизма: первая посылка - общеутвердительная; MаР.
Вторая посылка - общеутвердительная; SaM.
Заключение - общеутвердительная; SaP.
Силлогизм построен по первой фигуре, модус ААА − правильный, правила фигур, терминов и посылок не нарушены, заключение правильное.
В силлогистических умозаключениях наиболее распространенными ошибками являются следующие:
1. Когда нарушается тождество понятий, образующих средний термин. Например:
Все вулканы – горы.
Гейзеры – вулканы.
Гейзеры – горы.
Внешне понятие «вулканы», образующие средний термин тождественны, но по употребляемому смыслу они разные: в большей посылке понятие «вулканы» употреблено в обыденном смысле, а в меньшей − как научный термин. В силлогизме стало четыре термина, поэтому заключение оказалось неправильным.
2. Когда вывод делается по первой фигуре с меньшей отрицательной посылкой. Например:
Все рыбы размножаются икрой.
Лягушки − не рыбы.
Лягушки не размножаются икрой.
3. Когда вывод делается по второй фигуре с двумя утвердительными посылками. Например:
Все металлы проводят электричество.
Графит проводит электричество.
Графит – металл.
Здесь нарушено правило второй фигуры силлогизма. Следует помнить, что в рассуждениях дедуктивного вида нельзя в заключении говорить о большем множестве предметов, чем то, которое нам дано в посылках. Термин, не распределенный в посылках, не может быть распределен в заключении.
Силлогизм является элементарным выводом, неразложимым на более простые умозаключения. Но чтобы получить новое знание, иногда требуется выстроить цепь из звеньев, представляющих собой простые силлогизмы, в которых заключение предшествующего силлогизма становится одной из посылок последующего. Такая цепь называется полисиллогизмом. Если заключение предыдущего силлогизма поставить на место большей посылки последующего, то такой полисиллогизм называется прогрессивным, если же поставить на место меньшей посылки, − регрессивным. Пример прогрессивного силлогизма:
Все металлы поддаются термообработке.
Медь – металл.
Медь поддается термообработке.
Медь поддается термообработке.
Эта болванка из меди.
Эта болванка поддается термообработке.
Пример регрессивного силлогизма:
Все болванки поддаются термообработке.
Некоторые заготовки – болванки.
Некоторые заготовки поддаются термообработке.
Энтимемы
В практике нашего мышления, как обыденного, так и научного, мы пропускаем либо одну из посылок, либо заключение. Такие силлогизмы, в которых та или иная часть не выражена в явной форме, называются энтимемами. Особенно это заметно в пословицах, которые имеют двухчастную форму: «тише едешь − дальше будешь» и тех высказываниях, где присутствуют модальности (так как, поскольку, поэтому и т. д.): «это вещество неизвестно науке, поскольку его химические характеристики не укладываются в Периодическую таблицу».
Для того, чтобы проверить правильность вывода, необходимо восстановить пропущенные части силлогизма и проверить, нет ли нарушений правил фигур, терминов и посылок. При определении пропущенных частей будем руководствоваться грамматическими признаками. Суждение, являющееся посылкой, можно обнаружить за грамматическими союзами «так как», «поскольку», «ибо» и т. п. Определив посылку, следует выяснить, большая она или меньшая. Если в ней находится предикат заключения, то она большая, а если субъект заключения, − то меньшая. Затем следует восстановить недостающую посылку. Для этого надо соединить предикат заключения (для большей посылки) или субъект заключения (для меньшей посылки) со средним термином. При этом необходимо следить, чтобы при отрицательном заключении одна из посылок была отрицательной, а при утвердительном заключении, чтобы обе посылки были утвердительными.
Сориты
Иногда в полисиллогизмах одна из посылок может быть в неявной форме, то есть пропущенной. В этом случае эти силлогизмы называются соритами. В цепи силлогизмов, начиная со второго, пропущена меньшая или большая посылка. При ближайшем рассмотрении сориты всего лишь соединение простых силлогизмов, выраженных в форме энтимем. То есть заключение, полученное в результате вывода первого силлогизма, становится меньшей (или большей) посылкой следующего силлогизма и так далее до последнего в этой цепи силлогизма. Например:
Три − нечетное число.
Все нечетные числа − натуральные числа.
Все натуральные числа − рациональные числа.
Все рациональные числа − действительные числа.
Три − действительное число.
Здесь мы имеем дело с пропущенной меньшей посылкой. Попробуем пропустить большую посылку, начиная со второго силлогизма:
Все рациональные числа − действительные числа.
Все натуральные числа − рациональные числа.
Все нечетные числа − натуральные числа.
Три − нечетное число.
Три − действительное число.
Первый сорит можно представить в виде следующей схемы:
А есть В или в виде цепи простых силлогизмов:
В есть С 1. А есть В; В есть С; следовательно, А есть С.
С есть D 2. А есть С; С есть D; следовательно, А есть D.
D есть Е 3. А есть D; D есть Е; следовательно, А есть Е.
А есть Е
Второй сорит −по схеме:
D есть Е или в виде цепи простых силлогизмов:
С есть D 1. D есть Е; С есть D; следовательно, С есть Е.
В есть С 2. С есть Е; В есть С; следовательно, В есть Е.
А есть В 3.В есть Е; А есть В; следовательно, А есть Е.
А есть Е
Разделительные силлогизмы
Если в силлогизме одна из посылок является дизъюнктивным суждением, а другая посылка и вывод − категорические суждения, то такие силлогизмы называются разделительными. Вывод в разделительном умозаключении основывается на знании того, что перечисляемые в дизъюнктивном суждении признаки по отношению к предмету мысли являются несовместимыми (закон исключенного третьего) и полностью исчерпывают для данного случая все вероятные признаки предмета суждения.
Простые разделительно-категорические силлогизмы имеют два модуса:
1) утверждая-отрицающий (modus ponendo tollens)
А есть либо В, либо С.
А есть В.
А не есть С;
2) отрицая-утверждающий (modus tollendo ponens)
А есть либо В, либо С.
А не есть В.
А есть С.
В этих силлогизмах встречаются две ошибки. Одна называется «смешение соединительно-разделительного смысла с чисто разделительным». Например, если в соединительно-разделительной посылке говорится, что «плохая учеба студента N объясняется либо отсутствием хорошей школьной подготовки, либо халатным отношением к учебе», то это еще не означает невозможности этих двух признаков одновременно, ибо по утверждая-отрицающему модусу вторая посылка «плохая учеба студента N объясняется отсутствием хорошей школьной подготовки» приводит к заключению «следовательно, плохая учеба студента N не объясняется халатным отношением к учебе».
Вторая ошибка называется «неполное деление». Эта ошибка проявляется там, где в разделительной посылке мы укажем неполный перечень всех возможных предикатов. Например, в посылке «А есть либо В, либо С, либо D» мы в виде разделительной посылки возьмем «А есть либо В, либо С», а в виде категорической − «А не есть В», то заключение «А есть С» будет ошибочным, поскольку предикат D отсутствует и информация о признаках субъекта становится неполной.
Условные силлогизмы
Если в силлогизме обе посылки взяты как условные суждения, то заключение также будет условным суждением, а силлогизм будет опосредованным условным умозаключением.
Если А есть В, то С есть D.
Если С есть D, то Е есть F.
Если А есть В, то Е есть F.
То, о чем говорится в следствии (консеквенте) первой посылки, является содержанием основания (антецедента) второй посылки и обусловливает существование того, о чем говорится в следствии второй посылки. В силу этого в заключении мы можем утверждать, что то, о чем говорится в основании первой посылки, обусловливает содержание того, о чем говорится в следствии второй посылки. Иными словами, следствие следствия есть следствие основания. Это положение называется аксиомой условного силлогизма.
На базе разделительных и условных силлогизмов можно построить разделительно-условное и условно-категорическое умозаключения.
А). Разделительно-условное умозаключение состоит из разделительного суждения (первая посылка) и условных суждений (вторая и следующие посылки, число которых равно числу членов деления разделительной посылки).
Разделительно-условное умозаключение имеет два модуса: а) простой и б) сложный.
а) А есть либо В, либо С. б) А есть либо В, либо С.
Если А есть В, то А есть Р. Если А есть В, то А есть Р.
Если А есть С, то А есть Р.Если А есть С, то А есть М.
А есть К; А есть либо Р, либо М.
Из формулы простого модуса видно, что в условных суждениях, следствия (консеквенты) одинаковые при разных основаниях (антецедентах). В силу этого заключение простого модуса выражается простым категорическим суждением.
Из формулы сложного модуса видно, что в условных суждениях, при разных основаниях (антецедентах) следствия (консеквенты) также разные. В силу этого заключение простого модуса выражается сложным разделительным суждением.
Чтобы получить в выводе сложного суждения не разделительное, а категорическое суждение, надо заключение сложного модуса сделать либо посылкой простого модуса, либо посылкой отрицая-утверждающего модуса (modus tollendo ponens) разделительного умозаключения.
А есть либо В, либо С.
Если А есть В, то А есть Р.
Если А есть С, то А есть М.
А есть либо Р, либо М.
Если А есть Р, то А есть R.
Если А есть М, то А есть R.
А есть R.
Б). Условно-категорическое умозаключение состоит из условного суждения первой посылки и категорического суждения второй посылки. Заключение также категорическое суждение.
Условно-категорическое умозаключение имеет два вида. В первом виде одна из посылок представляет собой выделяющее условное суждение. Во втором виде одна из посылок представляет собой невыделяющее условное суждение.
Выделяющее условное суждение имеют два модуса а) утверждающий (modus ponens) и б) отрицающий (modus tollens):
а) Если А есть В, то С есть D. б) Если А есть В, то С есть D.
А есть В.С не есть D.
С есть D. А не есть В.
В утверждающем модусе вывод строится от утверждения основания к утверждению следствия. В отрицающем модусе вывод строится от отрицания следствия к отрицанию основания.
Следует знать, что выводы, построенные от отрицания основания к отрицанию следствия и от утверждения следствия к утверждению основания, не дают достоверных заключений. Например: «Если она богата, то она носит бриллианты. Она не богата. Следовательно, она не носит бриллианты». Вывод о том, что она не носит бриллианты, будет недостоверным.
Точно так же будет недостоверным вывод в следующем умозаключении: «Если она богата, то она носит бриллианты. Она не носит бриллианты. Следовательно, она не богата».
Причиной недостоверности приведенных выводов заключается в том, что в невыделяющем условном суждении то, о чем говорится в основании, является достаточным, но не необходимым условием для существования того, о чем говорится в следствии, а то, о чем говорится в следствии, является необходимым, но не достаточным условием для того, о чем говорится в основании.
Условно-категорическое умозаключение с выделяющей условной посылкой дает достоверные выводы в четырех случаях:
1. От утверждения основания к утверждению следствия.
2. От отрицания следствия к отрицанию основания.
3. От отрицания основания к отрицанию следствия.
4. От утверждения следствия к утверждению основания.
Выводы от утверждения основания к утверждению следствия и от утверждения следствия к утверждению основания применяется для доказательства того, что установленная закономерность имеет место в данном конкретном случае.
Выводы от отрицания следствия к отрицанию основания и от отрицания основания к отрицанию следствия применяется для доказательства того, что установленная закономерность неприменима в данном конкретном случае. Следует отметить, что выводы от отрицания следствия к отрицанию основания часто применяются при опровержении ошибочных аргументов (см. главу «Доказательство и опровержение).
В). Умозаключение отношений − это такие умозаключения достоверности, у которых посылки и заключение являются суждениями отношений. Умозаключение отношений имеют два вида: а) умозаключение равенства и б) умозаключение степени.
а) А равно В б) А больше В
С равно ВВ больше С
А равно С А больше С
Отсюда следуют две аксиомы: 1). Умозаключения равенства: «Два предмета, равные в некотором признаке третьему предмету, равны в этом признаке и между собой». 2). Умозаключения степени: «Если степень обладания некоторым признаком у одного предмета больше, чем у другого предмета, а степень обладания этим же признаком у другого предмета больше, чем у третьего, то степень обладания этим же признаком у первого предмета больше, чем у третьего».
Все виды умозаключений, рассмотренные в этой главе, имеют ту особенность, что вывод у них идет от знания большей степени общности к знанию меньшей степени общности (дедукция), или от знания определенной степени общности к знанию той же степени общности (традукция).
Вопросы для самопроверки
10. Что такое силлогизм?
11. Что является выводным знанием?
12. Из каких элементов состоит простой категорический силлогизм?
13. Назовите правила терминов, правила фигур и правила посылок.
14. В чем разница между аналитическим и синтетическим суждениями?
Упражнения
А) Определите модальность суждения. Приведите их схемы.
Пример:
1). Ухта южнее Воркуты. – Суждение об отношении места. xRy = R(x,y).
2). Нет дыма без огня. – Суждение существования. Р не есть.
3). Всяк сверчок знай свой шесток. – Суждение долженствования. S должен P.
4). Жизнь – борьба. – Суждение атрибутивное. S есть P.
1). Прямая задача динамики – это задача нахождения зависимости a = a(t). 2). Тело находится в данной точке пространства. 3). Я раньше всех пришел. 4). Материя и её движение вечны. 5). Тело, на которое не действуют другие тела можно назвать свободным.
Б) Постройте схему сорита: «Если принципы управления страной ясны, то суждения правителя и подданных едины; если принципы правления неясны, то суждения правителя и подданных различны. Если суждения едины, то дела осуществляются. Если дела осуществляются, то в стране царит порядок; если же дела не осуществляются, то в стране царит смута. Если в стране порядок, это значит, что он покоится на суждениях семьи; если же в стране смута, это значит, что дела решаются одним правителем» («Книга правителя области Шан». М., 1993. С.167).
В). Постройте простой категорический силлогизм из энтимемы и проверьте его правильность: «Масло передает давление на стенки сосуда равномерно, поскольку оно – жидкость».
Г). Сделайте вывод из посылок и установите: следует ли умозаключение с необходимостью: «Только один из участников соревнований станет победителем, а Крымов не участник соревнований».
Д). Постройте силлогизм и выясните, какие правила силлогизма нарушены: «Некоторые студенты – неуспевающие. Назаров – не студент. Следовательно…».
§4. Индуктивные умозаключения
Мы уже говорили о направленности логического процесса, когда от знания большей степени общности человек переходит к знанию меньшей степени общности. Но процесс познания общего возможен лишь через познание единичного; а это значит, что перечисление единичных предметов и единичных признаков, а затем их обобщение, выведение общего класса требует иного метода − индуктивного. Умозаключение, в котором происходит переход от знания меньшей степени общности к знанию большей степени общности называется индуктивным (лат. induction − наведение). Более того, единичный факт по выделенному нами признаку может служить основанием индуктивному обобщению.
Разница между дедукцией и индукцией состоит в том, что дедукция бывает лишь изредка обобщающим умозаключением, когда как индукция является только обобщающим умозаключением. В индукции основой вывода является принцип причинно-следственной связи, или причинной зависимости, когда как дедукция доказывает обобщение независимо от этих принципов, и вывод делает только на основе установленных правил. В дедукции заключение следует из посылок с необходимостью, тогда как в индукции вывод следует с вероятностью, приближающейся либо к нулю, либо к единице, и только в полной индукции, когда определены все предметы данного класса и выбранный признак является общим и существенным для этого класса, вероятность достоверности вывода равна единице.
Индуктивные умозаключения делятся на индукции полную и неполную; неполная индукция делится на популярную и научную; научная индукция делится на системную и структурную:
|
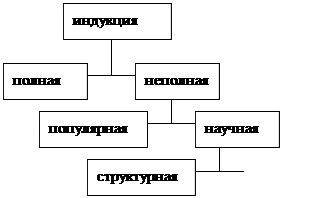 Рис.1
Рис.1
Общий вывод о классе предметов на основании существенного для всего класса признаков (предиката) и включает все предметы этого класса называется полной индукцией.
Схема полной индукции:
Ѕ1 – Р,
Ѕ2 – Р,
…….
Ѕn – Р,
Ѕ1^ Ѕ2^….. Ѕn есть все предметы класса А,
А есть Р.
Основание полной индукции достаточно для логического обоснования её вывода. Поэтому заключение полной индукции является достоверным из истинных, то есть достоверных для каждого предмета данного класса, предпосылок.
Достоверность выводов полной индукции делает возможным её применение во многих строгих доказательствах.
В подавляющем большинстве случаев мы не имеем возможности исследовать полностью выбранное нами множество предметов, и поэтому вынуждены обращаться к подмножеству, предполагая, что выделенный нами у части предметов признак присущ всем предметам данного класса.
Логический процесс, посредством которого мы заключаем, что признаки, присущие некоторым предметам класса, присущи всему классу называется неполной индукцией.
Схема неполной индукции:
Ѕ1 – Р,
Ѕ2 – Р,
…….
Ѕn – Р,
Ѕ1^ Ѕ2^….. Ѕn есть часть предметов класса А,
вероятно, А есть Р.
При заключениях по неполной индукции выводы складываются из двух составляющих: 1) вывода о возможности принадлежности данного признака, принадлежащего отдельному предмету класса всему классу предметов и 2) вывода о степени вероятности того, что каждый предмет этим признаком обладает.
Первая составляющая относится к наведению через простое перечисление, где не встречается противоречащих случаев. Процесс индукции через простое перечисление следующий: из принадлежности известного признака всем известным нам предметам данного класса делается вывод, что этот признак принадлежит всем предметам того же класса.
Вторая составляющая исследует те обстоятельства, при которых возможна обусловленная связь между признаками и предметами. Индукция выражает утверждение, что все случаи рассматриваемого явления или сопутствуют, или предшествуют, или последуют другому явлению. Эту связь мы начинаем выделять по тому признаку, который становится основанием нашего рассуждения.
Индукция через простое перечисление, где не встречается противоречащих случаев, называется популярной. Примером популярной индукции являются народные приметы, которые основаны на соотнесении множества наблюдаемых рядоположенных явлений. Само понятие «примета происходит от слова «примечать», то есть наблюдать, и выражает постоянное отношение между наблюдаемыми явлениями и событиями. Если задумал рыть колодец, то ищи место, где растет крупнолистный щавель, вьется мелкая мошка и чаще всего сидят гуси и утки, заросли плауна – признак того, что почва богата алюминием. Календарные приметы – это памятная книжка наблюдений над природой, которые до сих пор находят применение в таких науках, как экология, метеорология, фенология и др. Но стоит появиться одному противоречащему случаю, как общий вывод оказывается несостоятельным, а индукция становится поспешным обобщением. Другой частой ошибкой неполной индукции является обобщение несущественных признаков.
Индукция, основанная на обобщении существенных и необходимых признаков у части предметов данного множества и делается вывод об их принадлежности всему множеству, называется научной.
В научной индукции также используются выводы на основании соотнесенности необходимых связей. Особенно, если исследуется причинно-следственная связь явлений. Именно на знание такой связи опираются научные выводы. Научная индукция не останавливается на повторяемости фактов, а выделяет необходимее признаки и связи предметов и явлений. Не случайно закон науки определяется как повторяющаяся, необходимая и существенная связь между наблюдаемыми процессами и явлениями.
Схема научной индукции:
Ѕ1 имеет необходимый и существенный признак Р,
Ѕ2 имеет необходимый и существенный признак Р,
…….
Ѕn имеет необходимый и существенный признак Р,
…….
Ѕ1^ Ѕ2^….. Ѕn есть часть предметов класса А,
вероятно, А есть Р.
В зависимости от методов, которые используются в научной индукции, она делится на системную и структурную.
В системной индукции используется метод отбора, селекции, который ориентирует на выявление предметов и явлений в конкретных обстоятельствах, их обобщение и анализ с последующим умозаключением. Отобранные предметы и явления с существенными признаками составляют систему исследуемого объекта. Системная индукция находит широкое применение в научной классификации, социологических исследованиях, аналитических обзорах и т.д.
В структурной индукции используется метод исключения, который устанавливает причинно-следственную связь предметов и явлений на основании предшествующих им событий и исключает не относящихся к ним обстоятельства. При этом причина и следствие выступают как способ связи, необходимой и существенной для этих предметов и явлений. Следует помнить, что не все предшествующие явления относятся к последующему явлению как его причина, так как после этого еще не значит по причине этого. Такая логическая ошибка лежит в основе суеверий и поспешных или случайных выводов.
Вопросы для самопроверки
1. Что отличает научную индукцию от популярной?
2. Чем отличается метод отбора от метода исключения?
3. Какому основному принципу подчиняется индукция?
4. Что является условием достоверного вывода?
Упражнения
А). Укажите, какие из приведенных умозаключений получены с помощью полной, а какие с помощью неполной индукции: 1). Все студенты нашей группы прошли практику. 2). Угол падения равен углу отражения. 3). Осы ядовиты. 4). Всякая материальная точка подчиняется закону изменения механической энергии.
Б). Укажите, какие народные приметы, полученные с помощью популярной индукции не противоречат научной индукции: 1). Бросай овес в грязь – будешь князь. 2) Черная кошка дорогу перебежала – быть несчастью. 3). Курица в пыли копошится – быть дождю. 4) Кока умывается – гость придёт.5). Тёплый дождь прошёл – грибы появятся.
§5. Методы установления причинной связи явлений
Среди различных форм связи и взаимозависимости явлений, наблюдаемых нами, одной из важнейших считается причинная связь. Суть этой связи в том, что каждое явление природы или общества всегда вызывается каким-либо другим явлением.
Причиной называется явление, вызывающее другое явление. Вызванное явление называется следствием.
Причинная связь является всеобщей, необходимой и существенной, то есть, закономерной. Причинная связь обладает свойством определенности и однозначности. Определенная причина производит определенное действие, причем одинаковые причины при одних и тех же условиях вызывают одно и то же действие.
В логике существуют простейшие приемы, или как их называют, методы, которые позволяют определить причинную зависимость явлений. Они широко применяются как в повседневных рассуждениях, так и в научных выводах.
В логике имеется пять методов установления причинной связи: сходства, различия, соединенный метод сходства и различия, сопутствующих изменений, остатков. Применяются эти методы как при определении причины, так и при определении следствия. Все они опираются на методы эмпирического познания – наблюдение и эксперимент.
Процедура определения причинной связи достаточно сложная. Ведь каждому явлению предшествует бесконечное множество явлений. Поэтому чтобы найти действительную причину, надо отбросить те, которые не влияют существенно на исследуемое явление. Достигается это сравнением случаев присутствия и случаев отсутствия явлений, в процессе сравнения исключаются все те обстоятельства, которые не могут быть причиной, а включаются только те, которые производят изменения.
При рассмотрении методов установления причинной связи в учебном курсе предполагается, что круг возможных причин уже определен и задача сводится к установлению действительной причины из всех выделенных нами заранее возможных причин.
Метод сходства
Этот метод представляет собой умозаключение, основанное на сравнении нескольких случаев наступления одного и того же явления и выявления действительной причины на основе единственного сходства. Например, возьмем некоторое явление а и сопровождающие его обстоятельства АВС. Чтобы воспользоваться методом сходства, рассмотрим другие обстоятельства, когда данное явление произошло при иных и лишь частично сходных обстоятельствах; допустим, при обстоятельствах АКМ. Сравнивая эти случаи и опираясь на правило причинной связи, согласно которому явление не может наступить при отсутствии его причины, мы можем заключить, что причиной а не могут быть обстоятельства ВС, поскольку они отсутствуют во втором случае, когда явление а опять произошло. То же самое мы можем сказать и об обстоятельствах КМ, так как их не было в первом случае, когда имело место явление а, следовательно, остается предположить, что причиной а является обстоятельство А.
Если два или более случаев наступления наблюдаемого явления сходны только в одном предшествующем обстоятельстве, то вероятно это обстоятельство и является причиной данного явления:
АВС – а,
АКМ – а,
вероятно, А есть причина а.
Используя метод сходства для определения причины исследуемого явления, следует помнить, что случаи этого явления как можно больше различались между собой в обстоятельствах; такой подбор значительно облегчает процесс нахождения причины и уменьшает число случаев, необходимых для вывода. К этому надо добавить, что рассуждение, которое приводит нас к заключению о причине исследуемого явления, справедливо только тогда, когда это явление происходит от одной причины.
Метод сходства широко применяется в обыденной жизни и науке лишь в первых шагах исследования как первичное предположение. Это предположение затем проверяется и обосновывается с помощью более точных методов установления причинной связи.
Метод различия
Для умозаключения по этому методу необходимо иметь два случая: случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает. При этом они подбираются так, чтобы были сходны во всех обстоятельствах, кроме одного. Сравнивая первый случай со вторым, мы на основании свойства причинной связи можем заключить, что различие их в причинах есть результат различия их обстоятельств. Например, явление а наступает при обстоятельствах АВС. Чтобы выяснить, какое из этих обстоятельств является действительной причиной явления а, мы создадим такую ситуацию, при которой все обстоятельства, кроме одного, присутствуют, и явление при этом отсутствует. Можно заключить, что второй случай отличается от первого тем, что среди предшествующих явлению обстоятельств отсутствует либо причина, либо необходимое условие. Отсюда следует правило: если случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает, совпадают во всех обстоятельствах, кроме одного, встречающегося только в первом случае, то эта единственная разница и есть следствие, или причина (или необходимая часть причины) явления:
АВС – а,
- ВС -,
вероятно, А есть причина а.
Из всех методов установления причинной связи явлений метод различия является наиболее эффективным. Он применяется не только для установления причины по известному следствию, но и для определения следствия известной причины.
По сравнению с методом сходства метод различия имеет ряд преимуществ. Если метод сходства опирается на наблюдение, то метод различия ‑ на эксперимент, который позволяет искусственно изменять условия явлений. К тому же при методе различия бόльшая, чем при методе сходства вероятность получения достоверных заключений. Для того, чтобы повысить вероятность достоверного вывода при методе различия, нужно лишь точно установить обстоятельства, при которых происходит исследуемое явление, и убедиться в том, что сравниваемые случаи различаются только в одном обстоятельстве, или в определенной совокупности обстоятельств; что эксперимент делает это вполне возможным.






