Сила тока (ток) I численно равна количеству электричества, проходящему через поперечное сечение проводника в единицу времени:

Если сила тока I =const, то
 ,
,
где S – площадь поперечного сечения проводника,
q - заряд частиц,
n - их концентрация.
Ток, текущий по участку однородного проводника, подчиняется закону Ома

где U – разность потенциалов на концах участка,
R – сопротивление этого участка.
Сопротивление проводника

где r – удельное сопротивление,
s – удельная проводимость,
l – длина проводника,
S – площадь поперечного сечения проводника.
Удельное сопротивление металлов зависит от температуры следующим образом:
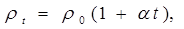
где r0 – удельное сопротивление при 0°С,
a – температурный коэффициент сопротивления.
Задача 29
Ток в проводнике меняется со временем по уравнению I=4+2t, где I[А], t[с]. Какое количество электричества пройдет через поперечное сечение проводника за время от t1 =2 с до t2 =6 с? При каком постоянном токе Io через поперечное сечение проводника за то же время проходит такое же количество электричества?
Дано:
I(t)=4+2t

| Решение: Сила тока I численно равна количеству электричества, проходящему через поперечное сечение проводника в единицу времени |

| 
|
Проинтегрируем это выражение
 I, A I, A
 i= 12 i= 12
 10 q 10 q
|
 I, A I, A
|


Если сила тока постоянна, то

Вычисления:

Ответ: при силе тока, меняющейся по закону I(t)=4+2t, количество электричества q, проходящее через поперечное сечение проводника от t1 до t2, равно q =48 Кл, при постоянном токе I0 =12 А через поперечное сечение проводника за то же время проходит такое же количество электричества.
Задача 30
Катушка из медной проволоки имеет сопротивление R =10,8 Ом. Масса медной проволоки m =3,41 кг. Какой длины l и какого диаметра d проволока намотана на катушку?
Дано:

| Решение:
По определению сопротивление проводника
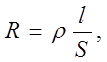 (1)
где S – площадь поперечного сечения, (1)
где S – площадь поперечного сечения,
|
| l, d –? | определяемая выражением |
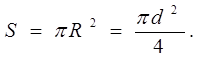
| (2) |
| l r |
| R m |
где r – удельное сопротивление.
По определению

| (3) |
где rm – плотность меди.
Выразим l из формулы (3), получаем:

| (4) |
Подставим (4) в (1), получаем

| (5) |
Подставим (2) в (5) и выразим d:

Найдем l, подставив (2) в (4), получаем
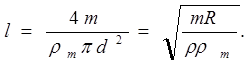
Вычисления:


Ответ: на катушку намотана проволока длиной l =501 м и диаметром d =1мм.
Задача 31
Вольфрамовая нить электрической лампочки при t1 =20 0C имеет сопротивление R1 =35,8 Ом. Какова будет температура t2 нити лампочки, если при включении в сеть напряжением U =120 В по нити идет ток I =0,33 A? Температурный коэффициент сопротивления вольфрама 
Дано:
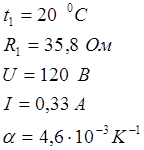
| Решение:
Сопротивление металлов зависит от температуры следующим образом
 (1)
Напишем это выражение для t1 (1)
Напишем это выражение для t1
 (1) (1)
|

| отсюда найдем R0 – сопротивление нити при t=0 °С. |

| (2) |
Перепишем выражение (1) для второго случая

| (3) |
По закону Ома для участка цепи имеем

| (4) |
Подставим (4), (2) в (3), получаем

отсюда выразим t2


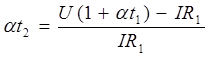

Вычисления:

Ответ: при включении нити лампочки в сеть ее температура станет равной t2 =2193 °C.
Задача 32
Найти падения потенциала U на сопротивлениях R1 =4 Ом, R2 =2 Ом и R3 =4 Ом, если амперметр показывает ток I1 =3A. Найти токи I2 и I3 в сопротивлениях R2 и R3.
| Дано: R1 =4 Ом R2 =2 Ом R3 =4 Ом I1 =3 А | Решение: Цепь состоит из двух участков: первый участок – резистор R1 второй участок – резисторы R2 и R3, соединенные параллельно. |
| I2, I3, U1, U2, U3 –? | Т. к. участки цепи соединены последовательно, то сила тока в них равна |
I1=I23=3A=Iобщ.
Рассмотрим второй участок. Т. к. резисторы соединены параллельно, то
I2+I3=I23=3A.
Найдем сопротивление этого участка


Сопротивление двух последовательно соединенных участков равно

| R2 I2 R1 U23 A I1 U1 R3 I3 |
Падение напряжения на всей цепи по закону Ома

Т. к. участки соединены последовательно, то
U1+U23=Uобщ.
Отсюда
U23=Uобщ–U1.
Падение напряжения на резисторе R1 будет равно по закону Ома
U1=I1R1.
В итоге получим

Падения напряжения на резисторах R2 и R3 равно
U2=U3=U23=4B,
т. к. они соединены параллельно.
Сила тока в сопротивлении R2 равна по закону Ома

Сила тока в сопротивлении R3 равна I3=I23–I2.
Вычисления:
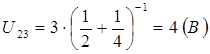


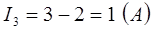
Ответ: падения напряжения на сопротивлениях R1, R2, R3 соответственно равны U1 =12 B, U2 = U3 =4 B, токи через резисторы R2 и R3 соответственно равны I2 =2A, I3 =1A.
Задача 33
Элемент, имеющий э.д.с. Е =1,1 В и внутреннее сопротивление r =1 Ом, замкнут на внешнее сопротивление R =9 Ом. Найти ток I в цепи, падение потенциала U во внешней цепи и падение потенциала Ur внутри элемента. С каким КПД h работает элемент?
| Дано: Е =1,1 В r =1 Ом R =9 Ом | Решение:
Для замкнутой цепи закон Ома имеет вид
 (1) (1)
|
I, Ur, U, 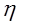 –? –?
| Отсюда найдем падение потенциала Ur и U, |
 E E
r I
R |
как произведение силы тока и сопротивления внутри элемента или внешнего сопротивления соответственно.
Преобразуем выражение (1)
Ir+IR=E.
Ur=E–IR. (2)
U=E–Ir. (3)
Подставим в выражения (2) и (3) формулу (1), получаем:


Найдем КПД источника.
КПД источника тока равен отношению мощности Р1, выделяемой внешним участком электрической цепи (полезной мощности), к полной мощности Р, развиваемой источником:

По определению

Тогда КПД источника

Согласно закону Ома для замкнутой цепи,

следовательно:

Таким образом, КПД источника тока зависит от значений сопротивления R внешнего участка цепи и внутреннего сопротивления r источника. Один и тот же источник тока в различных цепях работает с различным КПД, поэтому говорят не о КПД источника, а о КПД цепи. Разделив знаменатель и числитель на R, получаем:

Вычисления:




Ответ: ток в цепи составляет I =0,11 А, падение напряжения на внешнем сопротивлении составляет U =0,99 В, а на внутреннем – Ur =0,11 В. Элемент работает с КПД h =0,9.
Задача 34
Элемент с э.д.с. Е =1,6 В имеет внутреннее сопротивление r =0,5 Ом. Найти КПД h элемента при токе в цепи I =2,4 А.
| Дано: Е =1,6 В r =0,5 Ом I =2,4 A | Решение:
Для замкнутой цепи закон Ома имеет вид
 (2) (2)
|
| h –? | отсюда найдем внешнее сопротивление R. |
IR+Ir=E
 (2)
(2)
КПД источника равен отношению мощности Р1, выделяемой внешним участком электрической цепи (полезной мощности), к полной мощности Р, развиваемой источником:
 E E
r I
R |
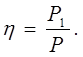
Исходя из формул Р1=I2R и Р=EI найдем h, зная, что I можно найти из формулы (1)
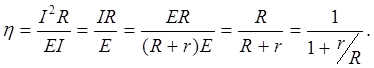
| (3) |
Подставим в (3) выражение (2), получаем

Вычисления:

Ответ: КПД элемента равен h =25%.
Задача 35
Считая сопротивление вольтметра Rv бесконечно большим, определяют сопротивление R по показаниям амперметра и вольтметра. Найти относительную погрешность  найденного сопротивления, если в действительности сопротивление вольтметра равно Rv. Задачу решить для Rv =1000 Ом и сопротивления а) R =10 Ом, б) R =100 Ом, в) R =1000 Ом.
найденного сопротивления, если в действительности сопротивление вольтметра равно Rv. Задачу решить для Rv =1000 Ом и сопротивления а) R =10 Ом, б) R =100 Ом, в) R =1000 Ом.
| Дано: Rv =1кОм а) R =10 Ом б) R =100 Ом в) R =1000 Ом | Решение:
Из закона Ома для постоянного тока найдем выражение для R

|

| Прологарифмируем данное равенство, получаем ln R =ln U -ln I, |
дифференцируем обе части полученного выражения:

переходим от бесконечно малых к конечным приращениям:
 E E
|

заменяя знак для получения максимальной погрешности.
Пренебрегая внутренним сопротивлением источника, считаем напряжение на резисторе и вольтметре одинаковым и равным э.д.с. источника Е, т. к. соединение резистора и вольтметра параллельное, отсюда U=constÞDU=0 и тогда  формула приобретает вид:
формула приобретает вид:

По закону Ома для цепи: сила тока в цепи до подключения вольтметра была равна

при подключении вольтметра она стала

где Rэкв – общее сопротивление внешней цепи.
Найдем его, зная, что вольтметр и сопротивление соединены параллельно


Тогда
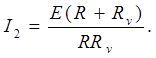
Так как Rэкв<R, то I2>I1 и можно записать, что
DI=I2–I1.
Получаем следующее выражение


Зная, что

найдем

Вычисления:



Ответ: относительная погрешность для сопротивлений R1 =10 Ом, R2 =100 Ом, R3 =1000 Ом соответственно равна  ,
,  ,
,  .
.
Задача 36
Считая сопротивление амперметра Ra бесконечно малым, определяют сопротивление R по показаниям вольтметра и амперметра. Найти относительную погрешность  найденного сопротивления, если в действительности сопротивление амперметра равно Ra. Решить задачу для RA =0,2 Ом и сопротивления а) R =1 Ом, б) R =10 Ом, в) R =100 Ом.
найденного сопротивления, если в действительности сопротивление амперметра равно Ra. Решить задачу для RA =0,2 Ом и сопротивления а) R =1 Ом, б) R =10 Ом, в) R =100 Ом.
| Дано: Rа =0,2 Ом а) R =1 Ом б) R =10 Ом в) R =100 Ом | Решение:
Из закона Ома для постоянного тока найдем выражение для R

|

| Прологарифмируем данное равенство, получаем:

|
Дифференцируем обе части полученного выражения

Переходим от бесконечно малых к конечным приращениям:

 E E
|
Заменяем знак “–” на знак “+” для получения максимальной погрешности:
 (1)
(1)
Так как амперметр присоединен последовательно к сопротивлению, то сила тока I=const, т. е.
I1=I2 Þ DI=0,
зная это, перепишем выражение (1):
 (2)
(2)
Из закона Ома для полной цепи найдем напряжение U1 на резисторе R1, исключая сопротивление амперметра

с амперметром, соединенным последовательно, напряжение в цепи будет равным

Зная, что

найдем DU

Подставим полученное выражение в (2), получаем

Вычисления:
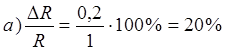


Ответ: относительная погрешность для сопротивлений R1 =1 Ом, R2 =10 Ом, R3 =100 Ом соответственно равна 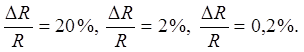
Задача 37
Два параллельно соединенных элемента с одинаковыми э.д.с. Е1=Е2 =2В и внутренними сопротивлениями r1 =1 Ом и r2 =1,5 Ом замкнуты на сопротивление R =1,4 Ом. Найти ток I в каждом из элементов всей цепи.
| Дано: Е1=Е2 =2 В r1 =1 Ом r2 =1,5 Ом R =1,4 Ом | Решение: Обозначим направления токов и выберем направления обхода контуров так, как показано на рисунке. По первому правилу Кирхгофа составим уравнение для узла А: |
| I –? I1 –? I2 –? | 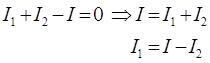
|
     E1r1 E1r1
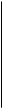       B C
I1 E2r2
A D B C
I1 E2r2
A D
   I2 R
F E I2 R
F E
|
По второму правилу Кирхгофа составим уравнение для контуров BCEF и ADEF соответственно:

Для нахождения I, I1, I2 найдем решение системы


Получим
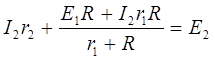





Вычисления:
 ;
; 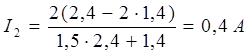

Ответ: токи I1, I2 в каждом из элементов Е1 и Е2 соответственно равны I1 =0,6 A, I2 =0,4 A и ток во всей цепи равен I =1 A.
Задача 38
Два последовательно соединенных элемента с одинаковыми э.д.с. Е1=Е2 =2 В и внутренними сопротивлениями r1 =1 Ом r2 =1,5 Ом замкнуты на внешнее сопротивление R =0,5 Ом. Найти разность потенциалов U на зажимах каждого элемента.
| Дано: Е1=Е2 =2 В r1=1 Ом r2 =1,5 Ом R =0,5 Ом | Решение: Если э.д.с. Е1, Е2,...,Еn и внутреннее сопротивление r1, r2,...,rn источников тока, соединенных последовательно но различны, то сила тока: |
| U1, U2 –? | 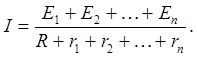
|
  E1 E2 E1 E2
       A B
r1 r2
R
D C A B
r1 r2
R
D C
   I I

|
По второму правилу Кирхгофа составим уравнение для контура ABCD, выбрав направление обхода против часовой стрелки, т.е.
 (1)
(1)
В нашем случае из (1) вытекает, что

Разность потенциалов на зажимах первого элемента


Разность потенциалов на зажимах второго элемента

Вычисления:


Ответ: разность потенциалов на зажимах первого и второго элементов U1 и U2 соответственно равны U1 =0,66 B и U2 =0 B.
Задача 39
Батарея с э.д.с. Е =20 В, амперметр и реостаты с сопротивлениями R1 и R2 соединены последовательно (см рисунок). При выведенном реостате R1 амперметр показывает ток I =8 А, при выведенном реостате R2 — ток I =5 А. Найти сопротивления R1 и R2 реостатов и падение потенциала U1 и U2 на них, когда реостат R1 полностью включен.
| Дано: E =20 B I1 =8 A I2 =5 A | Решение: Рассмотрим электрическую цепь при выведенном реостате, когда его сопротивление равно нулю. |
| R1, R2, U1, U2 –? | По закону Ома для полной цепи |
| E A R1 R2 |
 (1)
(1)
Рассмотрим случай, когда реостат в введенном состоянии, т.е. когда его сопротивление равно R.
По закону Ома для полной цепи:
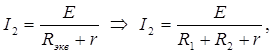 (2)
(2)
где Rэкв – внешнее сопротивление цепи, определяемое как Rэкв=R1+R2, т.к. соединение последовательное.
Из того факта, что соединение резисторов последовательное, вытекает тот факт, что
| U2+U1=E | (3) |
(по условию сопротивление батареи в расчет не принимается).
По закону Ома для участка цепи можно найти R1 и R2
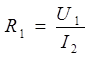
| (4) |

| (5) |
Подставим в (2) формулу (1), получаем:


| (6) |
Приравняв формулы (6) и (4), получаем:


| (7) |
Подставляя выражение (7) в (3), получаем:


Подставляя полученные нами выражения для U1 и U2 в формулы (5) и (4), получаем

Вычисления:


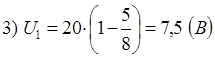

Ответ: падение потенциала U1 и U2 на сопротивлении и реостате, который полностью включен, равно соответственно U1 =7,5В, U2 =12,5B, сопротивление резистора R2 и включенного реостата равны соответственно R2 =2,5 Ом R1 =1,5 Ом.
Задача 40
Напряжение на зажимах элемента в замкнутой цепи U =2,1 В, сопротивление R1 =5 Ом, R2 =6 Ом и R3 =3 Ом. Какой ток показывает амперметр?
| Дано: U =2,1 B R1 =5 Ом R2 =6 Ом R3 =3 Ом | Решение: Напряжение на зажимах источника, замкнутого проводником с сопротивлением R, равно U=IR, в нашем случае R – это Rэкв, т.е. общее сопротивление |
| I3 –? | резисторов, а I – сила тока на резисторе R1, т.е. |
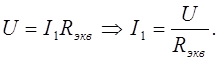
Найдем внешнее сопротивление цепи Rэкв.
 E E
R1 R2
D I3 C
R3 |
Так как резисторы R2 и R3 соединены параллельно, то, во-первых,
I1=I2+I3,
во-вторых, результирующее сопротивление этой батареи резисторов равно

Т. к. результирующее сопротивление соединено с R1 последовательно, то

Из цепи выделим контур ABCD и выберем направление обхода контура (по часовой стрелке).
По второму правилу Кирхгофа составим уравнение для этого контура:

или по закону Ома, так как U2=U3, то I2R2=I3R3
Составим систему уравнений
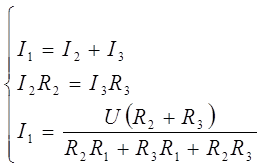

Отсюда

Отсюда

Вычисления:

Ответ: амперметр показывает на резисторе R3 ток, равный I3 =0,2 A.
Задача 41
Э.д.с. батареи Е =100 В, сопротивление R1=R3 =40 Ом, R2 =80 Ом, R4 =34 Ом. Найти ток I2, текущий через сопротивление R2, и падение напряжения U2 на нем.
| Дано: Е =100 В R1=R3 =40 Ом R2 =80 Ом R4 =34 Ом | Решение:
По закону Ома для замкнутой цепи
 (1) (1)
|
| I2,U2 –? | т.к. внутренним сопротивлением r можно пренебречь. |
Ток, текущий через сопротивление R4, равен I, так как цепь неразветвлена.
Выделим из цепи контур ABCD. Обозначим направление токов и выберем направление обхода контура.
| A E B R1 R2 I2 R3 R4 D C I4 |
По второму правилу Кирхгофа составим уравнение
IR4+U2=E,
где U2 – падение потенциала на резисторе R2.
Отсюда
U2=E–IR4 (2)
Для нахождения силы тока I найдем внешнее сопротивление цепи
Резисторы R1, R2, R3 соединены параллельно, и, значит, их результирующее сопротивление может быть найдена как

Отсюда

Результирующее сопротивление подключено последовательно с резистором R4, и, значит,
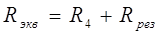
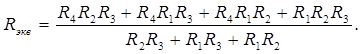 (3)
(3)
Подставим (1), (3) в (2), получаем:

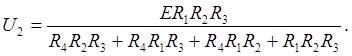 (4)
(4)
По закону Ома для участка цепи найдем, что
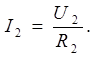 (5)
(5)
Подставим (4) в (5), получаем

Вычисления:


Ответ: падение потенциала на резисторе R2 равно U2 =32 В, ток, текущий через этот резистор, равен I2 =0,4 А.
Задача 42
Сопротивление R1=R2=R3 =200 Ом, сопротивление вольтметра Rv =1000 Ом. Вольтметр показывает разность потенциалов U =100 B. Найти э.д.с. Е батареи.
| Дано: R1=R2=R3 =200 Ом U =100 В Rv =1000 Ом | Решение: Обозначим направления токов и выберем направление обхода контура, как показано на рисунке |
| Е –? | По первому правилу Кирхгофа составим |
уравнение для узла С:
 (1)
(1)
       E E
  B C B C
  IV IV
    R1 V R2 I2 R1 V R2 I2
 I1 I1
R3
|
 По второму правилу Кирхгофа составим уравнение для контура ABC:
По второму правилу Кирхгофа составим уравнение для контура ABC:
 (2)
(2)
По закону Ома для участка цепи найдем, что
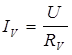 (3)
(3)
и
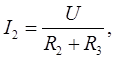 (4)
(4)
т.к. ток на резисторе R3 равен I2, поскольку соединение последовательное, подставим (3) и (4) в (1), получаем, что
 (5)
(5)
Подставим (5) в (2), зная, что RVIV=U, отсюда
 .
.
Вычисления:
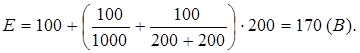
Ответ: э.д.с. батареи равна Е =170 В.







 1 t, c
1 t, c
 q
q
 1 t, c
1 t, c



 A
A 


 R
R

 V
V


 R
R
 A
A

 V
V






 A I2 B
A I2 B I1
I1 A
A




 A
A
