Задача 21
Площадь пластин плоского воздушного конденсатора S =1м2, расстояние между ними  Найти емкость С этого конденсатора.
Найти емкость С этого конденсатора.
Дано:

| Решение:
Если на единице поверхности обкладок имеется заряд s и диэлектриком является вакуум, то полное напряжение между обкладками равно

|
| С –? | где d – расстояние между пластинами. |
d
S
-q +q |
Если площадь каждой пластины равна S, то полный заряд пластины есть
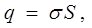
поэтому

Вычисления:

Ответ: емкость плоского воздушного конденсатора равна С =5,9 нФ.
Задача 22
Конденсатор предыдущей задачи заряжен до разности потенциалов U =300В. Найти поверхностную плотность заряда на его пластинах.
Дано:
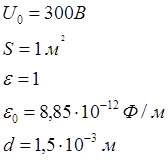
| Решение: Вычислим разность потенциалов между положительно заряженной пластиной и произвольной точкой, удаленной на расстояние х от нее. Напряженность поля в плоском конденсаторе выражается формулой |
 –? –?
| 
|
d
S
 -q +q
-q +q
|
Поэтому

Полная разность потенциалов U0 между электродами равна

Вычисления:

Ответ: поверхностная плотность заряда на пластинах конденсатора 
Задача 23
Площадь пластин плоского воздушного конденсатора  , расстояние между ними d =5 мм. К пластинам конденсатора приложена разность потенциалов
, расстояние между ними d =5 мм. К пластинам конденсатора приложена разность потенциалов 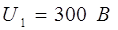 . После отключения конденсатора от источника напряжения пространство между пластинами конденсатора заполняется эбонитом. Какова будет разность потенциалов
. После отключения конденсатора от источника напряжения пространство между пластинами конденсатора заполняется эбонитом. Какова будет разность потенциалов  между пластинами после заполнения? Найти емкости конденсатора
между пластинами после заполнения? Найти емкости конденсатора 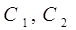 и поверхностные плотности заряда на пластинах до и после заполнения.
и поверхностные плотности заряда на пластинах до и после заполнения.
Дано:

| Решение:
В данном случае q1=q2, где q1 и q2 – заряды на пластинах конденсатора до и после заполнения эбонитом. Таким образом, q=const.
Следовательно, и поверхностная плотность заряда на пластинах

|

|
d
S
-q +q |
d
-q +q |
Так как

то до и после заполнения имеем
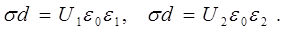
Учитывая, что s=const и d=const, получим

откуда

До и после заполнения эбонитом имеем

Поверхностная плотность заряда
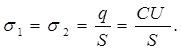
Вычисления:




Ответ: до и после заполнения эбонитом имеем 
Задача 24
Между пластинами плоского конденсатора, находящимися на расстоянии d =1 см друг от друга, приложена разность потенциалов U =100 В. К одной из пластин прилегает плоскопараллельная пластинка кристаллического бромистого таллия ( ) толщиной
) толщиной 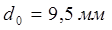 . После отключения конденсатора от источника напряжения пластинку кристалла вынимают. Какова будет после этого разность потенциалов между пластинами конденсатора?
. После отключения конденсатора от источника напряжения пластинку кристалла вынимают. Какова будет после этого разность потенциалов между пластинами конденсатора?
Дано:
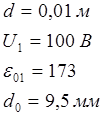
| Решение: Конденсатор, находящийся в положении 1, можно представить как батарею из двух последовательно соединенных конденсаторов с различной средой между обкладками. В этом случае одинаков для всех конденсато- |
| U2 –? | ров заряд q, равный полному заряду батареи, и мы |
можем написать

Напряжение батареи будет равно сумме напряжений на отдельных конденсаторах, т.е.

Следовательно,

Поэтому для емкости С всей батареи находим

 d
d
  С С
 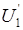 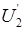 -q +q
-q +q
 d0 d0
 e e 01
e e 01
  U1 U1
|
 С¢ С¢
  d d
 +q -q +q -q
 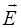 e=1
e=1
  U2 U2
|
т. е. 


| (1) |
Пусть С¢ – емкость конденсатора после вынимания пластины.
По определению
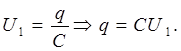
| (2) |
Подставим (1) в (2), получаем

Емкость конденсатора во втором положении
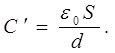
По закону сохранения заряда q=q¢, т. е.
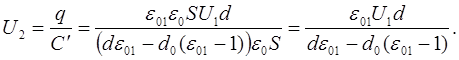
Вычисления:

Ответ: разность потенциалов станет 1,8 кВ.
Задача 25
Найти емкость С системы конденсаторов, изображенной на рисунке. Емкость каждого конденсатора С =0,5 мкФ.
| Дано: С =0,5 мкФ | Решение: Рассмотрим конденсаторы с емкостью С1 и С2, |
| С –? | соединенные параллельно, зная, |
что

| C1 C3 C2 |
найдем Срез получившейся батареи конденсаторов.
Рассмотрим батарею и конденсатор С3, они соединены последовательно. Зная, что при последовательном соединении

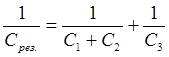

Вычисления:
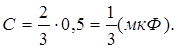
Ответ: емкость системы конденсаторов составляет  мкФ.
мкФ.
Задача 26
При помощи электрометра сравнивали между собой емкости двух конденсаторов. Для этого заряжали их до разностей потенциалов U1 =300 В и U2 =100 В и соединяли оба конденсатора параллельно. Измеренная при этом разность потенциалов между обкладками конденсатора оказалось равной U =250 В. Найти отношение емкостей 
| Дано: U1 = 300 В U2 = 100 В U = 250 В | Решение: Изобразим ситуацию до соединения (рис. а) и после него (рис. б). Используя определение емкости конденсатора, найдем за- |

| ряды конденсаторов до их соединения: |
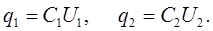
а) C1
      + - + -
 U1 U1
|
  б) C2 б) C2
+ -
U2
|
Согласно закону сохранения электрического заряда, общий заряд после их соединения равен сумме зарядов конденсаторов до соединения

Кроме того, при соединении параллельно их общий заряд равен сумме зарядов каждого конденсатора после соединения
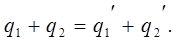
| (1) |
Но

где U – разность потенциалов между обкладками после их соединения.
| C1 + - C2 + - U |
Подставив значения q1, q2, q1¢, q2¢ в выражение (1), получим
 ,
,
поделим на С 2


Вычисления:

Ответ: отношение емкостей конденсаторов 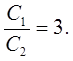
Задача 27
Пластины плоского конденсатора площадью  каждая притягиваются друг к другу с силой F =30 мН. Пространство между пластинами заполнено слюдой. Найти заряды q, находящиеся на пластинах, напряженность Е поля между пластинами и объемную плотность энергии поля.
каждая притягиваются друг к другу с силой F =30 мН. Пространство между пластинами заполнено слюдой. Найти заряды q, находящиеся на пластинах, напряженность Е поля между пластинами и объемную плотность энергии поля.
Дано:

| Решение:
1) Сила притяжения между пластинами плоского конденсатора
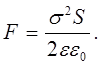 (1) (1)
| ||

| По определению поверхностная плотность заряда | ||

| (2) | ||
Подставим (2) в (1) и выразим q

| (3) |
2) Напряженность электрического поля внутри плоского конденсатора определяется формулой
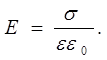
| (4) |
Подставим в (4) выражение (2), получим

| (5) |
3) Объемная плотность энергии электрического поля определяется формулой
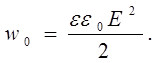
| (6) |
Подставим (5) в (6)

Вычисления:
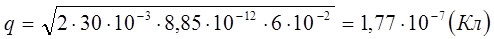
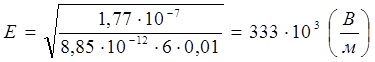

Ответ: заряд, находящийся на пластинах, равен  , напряженность поля между пластинами составляет
, напряженность поля между пластинами составляет 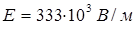 , объемная плотность энергии электрического поля равна
, объемная плотность энергии электрического поля равна 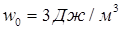 .
.
Задача 28
Плоский конденсатор заполнен диэлектриком, и на его пластины подана некоторая разность потенциалов. Его энергия при этом W =20 мкДж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую нужно было совершить против сил электрического поля, чтобы вынуть диэлектрик, А =70 мкДж. Найти диэлектрическую проницаемость диэлектрика.
Дано:

| Решение: Воспользуемся формулой, которая выражает энергию заряженного конденсатора через его |

| заряд и емкость |
 e
-q U +q
e
-q U +q
|
 e¢
-q U +q
e¢
-q U +q
|

| (1) |
Совершаемая работа против сил электрического поля идет на увеличение энергии конденсатора

| (2) |
Емкость плоского конденсатора с различными диэлектриками (в первом состоянии – диэлектрик, во втором состоянии – воздух), равны соответственно

| (3) |
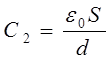
| (4) |
Подставим (3), (4), (1) в выражение, получаем

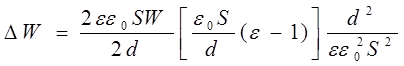


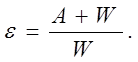
Вычисления:

Ответ: диэлектрическая проницаемость диэлектрика равна 
Тема 4









 e=1
e=1

 S
S