 (3)
(3)
По определению
FK=qE. (4)
Напряженность бесконечной плоскости
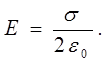 (5)
(5)
Подставим (5) в (4)
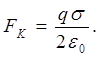 (6)
(6)
Подставляя (6) в (3), получаем


Вычисления:

Ответ: угол, который образует нить с плоскостью, равен  .
.
Задача 6
С какой силой Fl на единицу длины отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда 3 мкКл/м, находящиеся на расстоянии r1 =2 см друг от друга? Какую работу на единицу длины надо совершить, чтобы сдвинуть эти нити до расстояния r2 =1 см.?
Дано:

| Решение:
Напряженность поля, образованного заряженной бесконечно длинной нитью равна
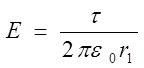 (1)
а) Сила, действующая (1)
а) Сила, действующая
| |
| F l –?, А l –? | на элементарный заряд dq, равна |
dF=E×dq (2)
Линейная плотность заряда равна
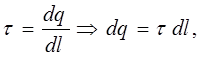 (3)
(3)
где dl – длина физически бесконечно малого отрезка нити,
dq – заряд, сосредоточенный на этом отрезке.
r1
|
Силу взаимодействия двух нитей можно найти по формуле с использованием формул (1), (2), (3)

где l – длина нити.
Отношение 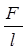 будет равно силе, с которой отталкиваются две нити на единицу длины
будет равно силе, с которой отталкиваются две нити на единицу длины
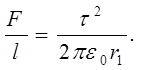 (1¢)
(1¢)
Вычисления:

б) Сила, действующая на отрезок нити равный dl равна
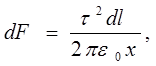 (4)
(4)
где х – расстояние между нитями.
Совершаемая при этом работа равна
dAl=Fldx. (5)
Интегрируем выражение (5)
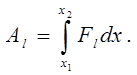 (6)
(6)
Подставляя в (6) формулу (1¢) при этом заменяя в (1¢) постоянный параметр r1 на изменяющийся параметр х, получаем

Вычисления:
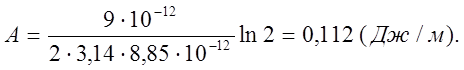
Ответ: две одноименные заряженные бесконечно длинные нити отталкиваются с силой Fl =8,1 Н/м, приходящейся на единицу их длины; чтобы сдвинуть эти две нити на 1 см, надо совершить работу Al =0,112 Дж/м, приходящуюся на единицу их длины.
Задача 7
В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля Е =60кВ/м. Заряд капли q =  . Найти радиус R капли.
. Найти радиус R капли.
Дано:
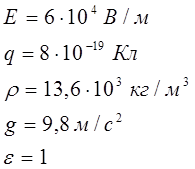
| Решение:
На шарик (каплю) действуют две силы: сила тяжести  и сила электростатического взаимодействия. При равновесии капли сумма проекций сил на вертикальное и горизонтальное направления равна нулю. и сила электростатического взаимодействия. При равновесии капли сумма проекций сил на вертикальное и горизонтальное направления равна нулю.
|
| R –? |  (1) (1)
|
       - -
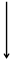  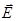  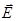
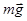
 + у + у
|
Найдем проекции векторов сил на ось Оу
Оу: mg–Fэл=0 Þ mg=Fэл (2)
По определению
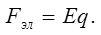
В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

По определению
 (3)
(3)
Подставим формулу (3) в (2), получаем
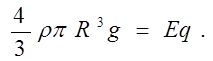

Вычисления:
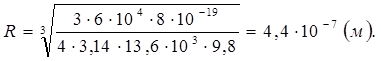
Ответ: радиус капли должен быть 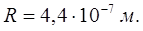
Задача 8
Кольцо из проволоки радиусом R =10 см имеет отрицательный заряд q =–5 нКл. 1) Найти напряженность Е электрического поля на оси кольца в точках, расположенных на расстояниях L равных 0, 5, 8, 10 и 15см. Начертить график Е=f(L). 2) На каком расстоянии L от центра кольца напряженность электрического поля будет иметь максимальное значение?
Дано:
| Решение:
1) Возьмем элемент кольца dl. Этот элемент несет заряд dQ.
Напряженность электрического поля в т. А, созданная этим элементом
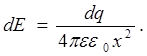 Она направлена по линии х, соединяющей элемент кольца dl с точкой А. Очевидно, для нахождения напряженности от всего кольца надо геометрически сложить dE от всех элементов. Вектор
Она направлена по линии х, соединяющей элемент кольца dl с точкой А. Очевидно, для нахождения напряженности от всего кольца надо геометрически сложить dE от всех элементов. Вектор 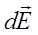 можно разложить на две составля- можно разложить на две составля-
|
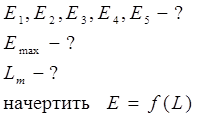
| ющие 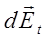 и и 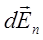 . Составляющие . Составляющие 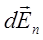 от каждых двух диаметрально противоположных элементов взаимно уничтожатся, и тогда от каждых двух диаметрально противоположных элементов взаимно уничтожатся, и тогда
|
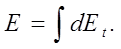
Составляющая
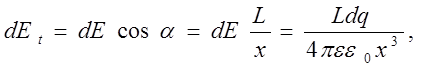
что дает
dq dl
x 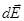 R
a
R
a  L
L 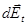
|
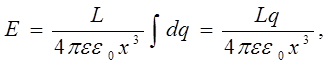
но 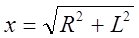 и окончательно
и окончательно
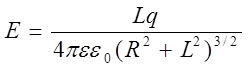 (1)
(1)
– напряженность электрического поля на оси кольца.
Если L>>R, то
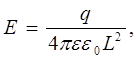
т. е. на больших расстояниях заряженное кольцо можно рассматривать как точечный заряд.
Подставляя в (1) числовые данные, получим соответственно

2) Выразим величины х и L через угол a. Имеем
R=sina, L=cosa.
Теперь формула (1) примет вид:
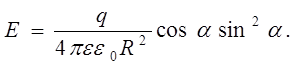
Для нахождения максимума величины Е возьмем производную 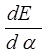 и приравняем ее нулю
и приравняем ее нулю
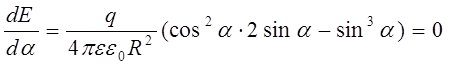
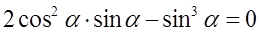
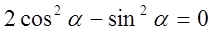
делим на cos2a
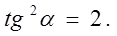
Тогда расстояние L точки А от центра кольца, на котором напряженность электрического поля максимальна, равно
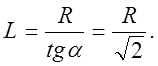
График E=f(L):
|
В нашем случае R =0,1 м и, следовательно,
Lm=7,1×10-2 м, Еmax=1732 В/м.
Ответ: напряженность электрического поля на 0 м; 0,05 м; 0,08 м; 0,1 м; 0,15м равна соответственно 0 В/м; 1609 В/м; 1714 В/м; 1590 В/м; 1152 В/м. Напряженность будет максимальной на расстоянии от центра 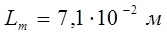 и равна Е =1732 В/м.
и равна Е =1732 В/м.
Тема 2
Потенциал
Разность потенциалов между двумя точками электрического поля определяется работой, которую надо совершить, чтобы единицу заряда перенести из одной точки в другую

Потенциал точечного заряда

где r – расстояние от заряда.
Напряженность электрического поля и потенциал связаны соотношением
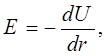
где U – разность потенциалов между пластинами конденсатора,
d – расстояние между ними.
Шаровой конденсатор
Разность потенциалов между внутренней сферой и какой-либо точкой внутри конденсатора, удаленной на расстояние r от центра конденсатора, равна
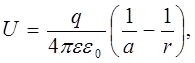
где а – радиус внутренней сферы.
Плоский конденсатор
Разность потенциалов между положительно заряженной пластиной и произвольной точкой, удаленной на расстояние х от нее, равна
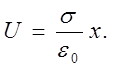
3) Цилиндрический конденсатор
Разность потенциалов между внутренним цилиндром и произвольной точкой между электродами равна

где а – радиус внутреннего цилиндра,
q1 – заряд внутреннего цилиндра на единицу длины.
Задача 9
Шарик массой m =40 мг, заряженный положительным зарядом q1 =1 нКл, движется со скоростью v =10 см/с. На какое расстояние r может приблизиться шарик к положительному точечному заряду q2 =1,3 нКл?
Дано:
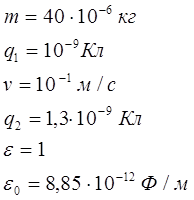
| Решение: Шарик, летящий в направлении точечного заряда, будет тормозиться полем до тех пор, пока не остановится на некотором расстоянии от него. После остановки шарик начнет двигаться назад и улетит в бесконечность. В момент остановки, когда скорость шарика относительно точечного заряда равна нулю, расстояние между ними |
 y
q2q1 y
q2q1
r |
| r –? | будет минимальным. |
Воспользуемся законом сохранения и превращения механической энергии
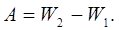 (1)
(1)
Работа внешних сил над электроном – работа сил поля равна

где j1 – потенциал поля заряда в той точке, где шарик обладал кинетической энергией 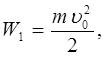
j2 – потенциал поля заряда в той точке, где шарик остановился W2 =0.
Если расстояние от заряда до указанных точек поля равно r и R, то, учитывая, что e =1, для потенциалов поля в этих точках получим
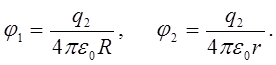
С учетом этих выражений для работы сил поля будем иметь
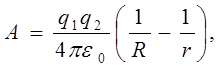
или
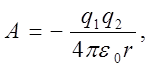 (2)
(2)
т. к. в данном случае R>>r.
Подставляем (2) в (1)

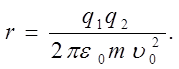
Вычисления:
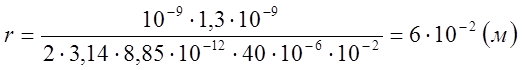
Ответ: шарик сможет приблизиться к положительному точечному заряду на расстояние 6 см.
Задача 10
На какое расстояние могут сблизиться два электрона, если они движутся навстречу друг другу с относительной скоростью 108 см/с?
Дано:
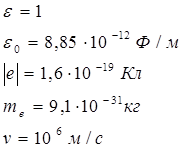
| Решение:
Будем считать, что один электрон неподвижен. Свяжем систему координат с неподвижным зарядом. Значит, второй электрон будет приближаться к первому со скоростью u =106 м/с.
Воспользуемся законом сохранения и превращения механической энергии:
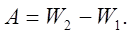 (1) (1)
|
| r –? |
 y y
|








 dl
dl
 dq dF x
dq dF x






 q1 q2 x
q1 q2 x



 r
r
