Введение
В предлагаемое учебное пособие вошли задачи по курсу общей физики (раздел “Электричество и магнетизм”), предназначенные для студентов физико-математических факультетов педагогических вузов. Задачи разделены по темам в соответствии с действующей программой по общей физике для подготовки бакалавров образования по направлениям “физика”, “математика”, “прикладная математика и информатика” и специалистов соответствующего профиля. В сборнике содержатся задачи трех уровней сложности, что упрощает его использование в сочетании с рейтинговой системой оценки знаний. Задачи первого (низшего) уровня сложности являются типовыми, они снабжены подробными решениями и предлагаются для воспроизведения студентам, претендующим на удовлетворительную оценку. Задачи второго и третьего уровней сложности предназначены для самостоятельного решения студентами, претендующими на более высокий рейтинг, требуют, как правило, проработки дополнительной литературы, и творческого подхода. Учебное пособие может быть полезно также учителям, работающим в школах с углубленным изучением физики и учащимся этих школ.
Тема 1
Закон Кулона Напряженность электрического поля
По закону Кулона сила, действующая между двумя заряженными телами, размеры которых малы по сравнению с расстоянием между ними, определяется формулой:
 ,
,
где q1 и q2 – электрические заряды тел,
r – расстояние между ними,
e – относительная диэлектрическая проницаемость среды,
e0 – электрическая постоянная, равная в СИ 8,85×10-12 Ф/м.
Напряженность электрического поля определяется формулой

где F – сила, действующая на заряд q.
Напряженность поля точечного заряда

Напряженность электрического поля от нескольких зарядов находится по правилу геометрических сложений полей.
По теореме Гаусса поток напряженности сквозь любую замкнутую поверхность

где S q – алгебраическая сумма зарядов, находящихся внутри этой поверхности.
При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами.
Напряженность поля, образованного заряженной бесконечно длинной нитью

где t – линейная плотность заряда на нити,
а – расстояние от нити.
Если нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити на расстоянии а от нее равна:

где q – угол между направлением нормали к нити и радиус-вектором, проведенным из рассматриваемой точки к концу нити.
Напряженность поля, образованного заряженной бесконечно протяженной плоскостью

где s – поверхностная плотность заряда на плоскости.
Если плоскость представляет собой диск радиусом R, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из центра диска на расстоянии а от нее,

Напряженность поля, образованного разноименно заряженными бесконечными плоскостями

Напряженность поля, образованного заряженным шаром

где q – заряд шара радиусом R,
r – расстояние от центра шара, причем r>R.
Задача 1
В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда. Найти напряженность Е электрического поля в центре шестиугольника при различных комбинациях в расположении этих зарядов. Каждый заряд 1,5 нКл, сторона шестиугольника 3 см.
Дано:

| Решение:
Возможны три варианта расположения зарядов в вершинах шестиугольника. Пусть
 .
Напряженность электрического поля в т. А является векторной суммой напряженностей .
Напряженность электрического поля в т. А является векторной суммой напряженностей

|
| Ерез –? | создаваемых в этой точке положи- |
тельными и отрицательными зарядами. Эти напряженности равны по модулю 
Рассмотрим случаи:
а) по принципу суперпозиции

| (1) |
угол между векторами 2 a =120°.
Т.к. векторы  и
и  ,
,  и
и  ,
,  и
и  сонаправлены, то их можно сложить.
сонаправлены, то их можно сложить.

|
| A |

| (2) |
-q4 +q2
  +q1 -q5
+q1 -q5
  -q6 +q3
-q6 +q3
|
Найдем результирующую напряженность между векторами  , она численно равна
, она численно равна

Вектор  направлен в противоположную сторону и, значит, уравнение (2) приобретает вид
направлен в противоположную сторону и, значит, уравнение (2) приобретает вид

учитывая, что  , приходим к выводу, что
, приходим к выводу, что
Ерез=0.
б) используя принцип суперпозиции:
 , ,
| (3) |
векторы  имеют взаимно противоположные направления и одинаковые значения, и уравнение приобретает вид:
имеют взаимно противоположные направления и одинаковые значения, и уравнение приобретает вид:
| Ерез=Е 2 +Е 5 = 2 Е 2, | (4) |
+q1 -q5
  -q4 -q6
-q4 -q6
   +q2 +q3
+q2 +q3
|

|
т. к.  сонаправлены и имеют равные значения, лежат на одной прямой.
сонаправлены и имеют равные значения, лежат на одной прямой.
 (5)
(5)
Подставим (5) в (4)

в) по принципу суперпозиции
 . .
| (6) |
+q3 -q4
+q1 -q6
|

|
Учитывая, что векторы  , и что они численно равны, выражение (6) можно переписать в виде:
, и что они численно равны, выражение (6) можно переписать в виде:
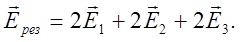
Результирующий вектор  лежит на
лежит на  (используя сложение правилом параллелограмма), угол между векторами
(используя сложение правилом параллелограмма), угол между векторами  равен 60°. Результирующая напряженность направлена от А к q5 и равна по модулю
равен 60°. Результирующая напряженность направлена от А к q5 и равна по модулю

 .
.
Ответ: напряженность в центре шестиугольника при трех вариантах расположения зарядов равна Е =0; Е =30 кВ/м; Е =60 кВ/м, соответственно.
Задача 2
Два точечных заряда q1 =7нКл, q2 =–14.7 нКл расположены на расстоянии r =5 см. Найти напряженность Е электростатического поля в точке, находящейся на расстоянии а =3 см от положительного заряда и b =4 см от отрицательного заряда.
Дано:

| Решение:
Рассмотрим общий случай при a – неизвестном.
Согласно принципу суперпозиции в точке А, напряженность  где где  – напряженности полей, создаваемых в этой точке зарядами q1 и q2 , соответственно. Вектор – напряженности полей, создаваемых в этой точке зарядами q1 и q2 , соответственно. Вектор  является диагональю параллелограмма является диагональю параллелограмма
|
| ЕА =? | со сторонами  . .
|
Воспользовавшись теоремой косинусов, найдем
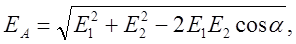
| (1) |
где  - модули векторов
- модули векторов  , соответственно.
, соответственно.
 , (2)
, (2)
применив теорему косинусов к треугольнику со сторонами r, a, b, получим
 ,
,
+q
a
A
 r
r 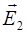
 b
-q
b
-q
|
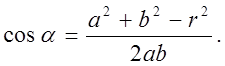 (3)
(3)
В нашем случае cos a = 0 и e = 1.
Подставим выражения (2) и (3) в формулу (1) и найдем ЕА


Вычисления:

Ответ: напряженность электростатического поля в точке А равна 
Задача 3
Два шарика одинаковых радиусов и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд Q нужно сообщить шарикам, чтобы сила натяжения нитей стала равной Т=98 мН? Расстояние от центра шарика до точки подвеса l =10 см, масса каждого шарика m =5г.
Дано:

| Решение:
На шарики действуют сила тяжести  , сила упругости , сила упругости  , сила кулоновского отталкивания , сила кулоновского отталкивания
 , (1)
где , (1)
где  – заряд, полученный каждым шариком после сообщения им заря- – заряд, полученный каждым шариком после сообщения им заря-
|
| q –? | да, равного q. |
     
y
|
При равновесии шарика сумма проекций сил на вертикальное и горизонтальное направления равна нулю.
 Спроецируем силы на оси координат Ох и Оу
Спроецируем силы на оси координат Ох и Оу
Ох: FK–Fупрsina=0
Oy: –Fупрcosa+mg=0.
Преобразуем уравнения
FK = Fупрsina. (2)
mg = Fупрcosa. (3)
По III закону Ньютона сила упругости и сила натяжения нити численно равны.
Из уравнения (3) получаем, что


под Т понимаем Fупр.
Найдем
 (4)
(4)
Из геометрических соображений видно, что
 (5)
(5)
Подставим формулы (1), (4), (5) в (2), получаем


Вычисления:

Ответ: чтобы сила натяжения нитей была равна Т нужно сообщить шарикам заряд, который равен 1,1 мкКл.
Задача 4
Два заряженных шарика одинаковых радиусов и массы подвешены на нитях одинаковой длины и опущены в жидкий диэлектрик, плотность которого равна  , а диэлектрическая проницаемость равна
, а диэлектрическая проницаемость равна  . Какова должна быть плотность
. Какова должна быть плотность  материала шариков, чтобы углы расхождения нитей в воздухе и в диэлектрике были одинаковы?
материала шариков, чтобы углы расхождения нитей в воздухе и в диэлектрике были одинаковы?
Дано:

| Решение:
Рассмотрим шарики, находящиеся в воздухе (e =1).
На шарик действует сила тяжести  , сила упругости , сила упругости  и сила куло- и сила куло-
|

| новского отталкивания  . При равнове- . При равнове-
|
     
y
|
сии шарика суммы проекций сил на вертикальное и горизонтальное направления равны нулю

Найдем проекции векторов сил на Ох и Оу
| Ох: FK–Fупрsina=0 ÞFK = Fупрsina. | (1) |
| Oy: –Fупрcosa+mg=0 Þ mg = Fупрcosa. | (2) |
Разделим почленно уравнение (1) на (2), получаем уравнение
 (3)
(3)
Из DАВС видно, что
 (4)
(4)
Подставим (3) в (4), получим
 a a
  l a l a

y
|
 (5)
(5)
Рассмотрим шарики, находящиеся в жидком диэлектрике.
При погружении шарика в диэлектрик на него начинает действовать выталкивающая сила Архимеда.
При равновесии шарика сумма проекций сил на вертикальное и горизонтальное направления равна нулю.

Найдем проекции векторов сил на оси Ох и Оу
| Ох: FK–Fупрsina=0 Þ FK = Fупрsina. | (6) |
| Oy: –Fупрcosa+mg+Fарх=0 Þ mg– Fарх = Fупрcosa. | (7) |
Поделим почленно уравнение (6) на (7), получим
 (8)
(8)
Подставим в (8) значение FK и выражение (4)
 (9)
(9)
Fарх численно равна
 (10)
(10)
Из (5), (9), (10) имеем





Ответ: плотность материала шарика должна быть получена из формулы 
Задача 5
На рисунке АА¢ — заряженная плоскость с поверхностной плотностью заряда 40 мкКл/м2 и В — одноименно заряженный шарик с массой 1г и зарядом 1нКл. Какой угол с плоскостью АА¢ образует нить, на которой висит шарик?
Дано:

| Решение:
На шарик действуют три силы: сила упругости  , сила тяжести , сила тяжести  и сила кулоновского отталкивания и сила кулоновского отталкивания  .
При равновесии шарика суммы проекций сил на горизонтальное и верти- .
При равновесии шарика суммы проекций сил на горизонтальное и верти-
|
| a –? | кальное направления равны нулю. |
        А¢ А¢
В y А |

Найдем проекции векторов на оси координат
Ох: FK–Fупр sin a=0
Oy: –Fупр cos a+mg=0.
FK = Fупр sin a. (1)
mg = Fупр cos a. (2)












 +q2
+q2 


 2 a
2 a 









 rx
rx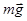







 a a
a a 







