Двойственные задачи линейного программирования.

Запишем в матричной форме.

; ; ; ;

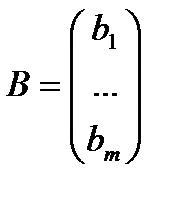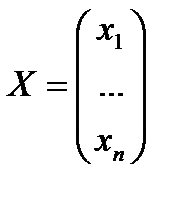Теорема: Задача, двойственная по отношению к двойственной, равносильна исходной задаче.

ò Рассмотрим исходную задачу и двойственную к ней. Преобразуем двойственную задачу к виду, которая имеет исходная.

→

Вводим вектор переменных U и строим двойственную задачу:

→ ; X=U^T. à

Двойственность в ЗЛП взаимна, т.е. двойственные задачи взаимно двойственны. Пару таких задач называют сопряжёнными задачами.

Модификация 1. Если в одной из двух сопряжённых задач ограничение имеет вид равенства, то в двойственной задаче соответствующая переменная неограничена по знаку.

Модификация 2. Если в одной из задач переменная не ограничена по знаку, то в двойственной задаче соответствующее ограничение имеет форму равенства.

Пример:

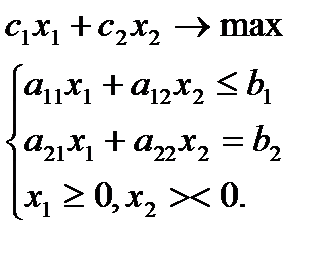
При решении:

x><0 → x` − x``=x, x`>0, x``>0;

 

Дискретные функции. Непрерывные функции.

Дискретные функции.

В GPSS два типа вычислительных объектов: арифметические переменные и функции. В моделях на GPSS значения функций (FNj) - это часто используемые стандартные числовые атрибуты, так как многие соотношения в системах могут быть описаны в терминах функциональной зависимости между двумя переменными. Каждая функция GPSS связывает значение аргумента функции, который представляет собой независимую переменную, со значениями зависимой переменной функции (FNj).

Запись определения функции имеет вид:

имя функции FUNCTION A,B

Имя функции должно записываться в поле метки оператора описания FUNCTION. Поле A оператора FUNCTION должно содержать аргумент (независимую переменную) функции. Аргументом может быть любой из стандартных числовых атрибутов или значение любой другой функции. Запись в поле B определяет тип и число точек функции X[i] и Y[i]. В этом поле для дискретных функций записывается символ D (признак дискретной функции) и целое число различных значений, которые может принимать случайная переменные. Далее следуют значения случайной переменной и соответствующие им значения функции распределения. Основной единицей информации записи значений функции является пара X_i, Y_i, где X_i - это i -я суммарная частота, Y_i - соответствующее значение случайной величины. Первый и второй элементы каждой основной единицы разделяются запятой. Последовательные основные единицы разделяются знаком " / ". Основные единицы должны следовать по порядку так, чтобы суммарные частоты шли в возрастающем порядке. Например:

PRFT FUNCTION RN4, D5

.15,2/.35,6/.6,8/.85,9/1,12

Функция имеет символическое имя PRFT. В качестве источника случайных чисел выступает RN4. Случайная величина имеет пять различных значений. Суммарные частоты и соответствующие им пять значений записаны как пять пар чисел. При записи пар, описывающих распределение, можно не записывать десятичную точку, если данные имеют целые значения. Ниже на рисунке приведена графическая интерпретация функции PRFT.

Предположим, что распределение интервалов приходов через определенный блок GENERATE не является равномерным. Для входов транзактов в модель через блок GENERATE пользователь в этом случае выполняет два действия:

1. Определяет функцию, описывающую соответствующее распределение интервалов времени.

2. В качестве операнда A блока GENERATE определяет функцию, а операнд B либо определяется по умолчанию, либо задается равным нулю.

Способ определения функции в блоке зависит от того, как задано имя функции: в символическом или числовом виде. Если имя числовое, то ссылка на функцию записывается как FNj, где j - номер функции. Если имя символическое, ссылка записывается в виде FN$ имя. Например, ссылка на функцию 16 может быть записана в виде FN16, а ссылка на функцию с символическим именем PRFT записывается как FN$PRFT. Приведем пример использования функции в блоке GENERATE. В таблице представлены интервалы времени между соседними моментами поступления транзактов.

Ниже приведен пример простейшей модели, использующей описанные функции в блоках GENERATE и ADVANCE. Единица модельного времени - 1 минута.

PRFT FUNCTION RN7,D4

.1,2/.4,3/.8,4/1,5

TFRP FUNCTION RN3,D6

.05,5/.17,6/.45,7/.75,8/.93,9/1,10

GENERATE FN$PRFT

SEIZE JOB

ADVANCE FN$TFRP

RELEASE JOB

TERMINATE

GENERATE 480

TERMINATE 1

Использование функций позволяет задавать различные формы дискретных распределений случайных значений интервалов поступления и задержки транзактов.

Непрерывные функции.

По определению дискретные случайные величины принимают конечное число различных значений, в то время как непрерывные - любое количество различных значений. Значения непрерывной функции, как и дискретной, определяются парами значений X_i, Y_i. В дискретной функции ее значения меняются скачком, в непрерывной - выполняется линейная интерполяция для пары точек, находящихся по краям того интервала значений суммарной вероятности, на которое указало случайное число. Непрерывная функция определяется с помощью символа С (в отличие от символа D для дискретных функций. Например:

PRFT FUNCTION RN4, C5

.15,2/.35,6/.6,8/.85,9/1,12

При моделировании существующих систем существует возможность оценить вид распределения и заложить его гистограмму в непрерывную функцию.

Включение непрерывных функций в блоки GENERATE и ADVANCE аналогично включению дискретных в эти же блоки (FN$ имя). Ниже приведен пример моделирования мнгоканального устройства с использованием функций двух видов. Единица модельного времени - 1 секунда. При этом известно непрерывное распределение времени обслуживания клиента (функция PRFT) и дискретное распределение прихода клиентов (функция TFRP).

PRFT FUNCTION RN2,C6

0.0,15/.07,30/.32,45/.73,60/.92,75/1.0,90

TFRP FUNCTION RN3,D6

.05,7/.17,12/.45,17/.75,22/.93,27/1,32

JOB STORAGE 3

GENERATE FN$TFRP

QUEUE JQE

ENTER JOB

DEPART JQE

ADVANCE FN$PRFT

LEAVE JOB

TERMINATE

GENERATE 28800

TERMINATE 1

Использование непрерывных функций позволяет задавать различные формы непрерывных распределений случайных значений интервалов поступления и задержки транзактов.

 

Дискриминантный анализ.

Дискриминантный анализ, как раздел многомерного статистического анализа, включает в себя статистические методы классификации многомерных наблюдений в ситуации, когда исследователь обладает так называемыми обучающими выборками ("классификация с учителем"). Например, для оценки финансового состояния своих клиентов при выдаче им кредита банк классифицирует их по надежности на несколько категорий по ряду признаков. В случае, когда следует отнести клиента к той или иной категории используют процедуры дискриминантного анализа. Очень удобно использовать дискриминантный анализ при обработке результатов тестирования. Так при выборе кандидатов на определенную должность можно всех опрошенных претендентов разделить на две группы - удовлетворяющих и неудовлетворяющих предъявляемым требованиям.

Все процедуры дискриминантного анализа можно разбить на две группы и рассматривать их как совершенно самостоятельные методы. Первая группа процедур позволяет интерпретировать различия между существующими классами, вторая - производить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат.

Пусть имеется множество единиц наблюдения - генеральная совокупность. Каждая единица наблюдения характеризуется несколькими признаками: x_ij - значение j -й переменной i -го объекта (i=1,..., n; j=1,..., p). Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом n_k, где k - номер подмножества (класса), k = 1,..., q.

Признаки, которые используются для того, чтобы отличать один класс (подмножество) от другого, называются дискриминантными переменными. Число объектов наблюдения должно превышать число дискриминантных переменных: p<n. Дискриминантные переменные должны быть линейно независимыми. Основной предпосылкой дискриминантного анализа является нормальность закона распределения многомерной величины. Это означает, что каждая из дискриминантных переменных внутри каждого из рассматриваемых классов должна быть подчинена нормальному закону распределения.

Основная идея дискриминантного анализа заключается в том, чтобы определить, отличаются ли совокупности по среднему какой-либо переменной (или линейной комбинации переменных), и затем использовать эту переменную, чтобы предсказать для новых членов их принадлежность к той или иной группе. Канонической дискриминантной функцией называется линейная функция:

d_km = β₀ + β₁*x_1km +... + β_p*x_pkm,

где:

d_km - значение канонической дискриминантной функции для m -го объекта в группе k (m = 1,..., n, k = 1,..., g);

x_pkm - значение дискриминантной переменной X_i для m -го объекта в группе k;

β₀,..., β_p - коэффициенты дискриминантной функции.

С геометрической точки зрения дискриминантные функции определяют гиперповерхности в p -мерном пространстве. В частном случае при p =2 она является прямой, а при p=3 -плоскостью.

Коэффициенты β_i первой канонической дискриминантной функции выбираются таким образом, чтобы центроиды (средние значения) различных групп как можно больше отличались друг от друга. Коэффициенты второй группы выбираются также, но при этом налагается дополнительное условие, чтобы значения второй функции были некоррелированы со значениями первой. Аналогично определяются и другие функции. Отсюда следует, что любая каноническая дискриминантная функция d имеет нулевую внутригрупповую корреляцию с d₁, d₂,..., d_g-1. Если число групп равно g, то число канонических дискриминантных функций будет на единицу меньше числа групп. Однако по многим причинам практического характера полезно иметь одну, две или же три дискриминантных функций. Тогда графическое изображение объектов будет представлено в одно–, двух– и трехмерных пространствах. Такое представление особенно полезно в случае, когда число дискриминантных переменных p велико по сравнению с числом групп g.

 

15.Задачи имитационного моделирования и принципы построения. Общий вид задачи имитационного моделирования.

Каждая модель или представление объекта средствами, отличными от его реального содержания есть форма имитации. Имитационное моделирование является весьма широким и недостаточно четко определенным понятием, имеющим очень большое значение для лиц, ответственных за создание и функционирование практически любых систем.

При имитационном моделировании динамические процессы объекта подменяются процессами, имитируемыми в абстрактной модели, но с соблюдением основных правил (режимов, алгоритмов) функционирования оригинала. В процессе имитации фиксируются определенные события и состояния или измеряются выходные воздействия, по которым вычисляются характеристики качества функционирования системы.

Все имитационные модели представляют собой модели типа так называемого " черного ящика ". Это означает, что они обеспечивают выдачу выходных параметров системы, если на ее взаимодействующие подсистемы поступают входные воздействия. Для моделирования необходимо создать модель и провести ее исследование. Перед созданием модели требуется конкретизировать цели моделирования. После исследования надо выполнить обработку и анализ результатов моделирования. Процесс создания моделей проходит несколько стадий. Он начинается с изучения (обследования) реальной системы, ее внутренней структуры и содержания взаимосвязей между ее элементами, а также внешних воздействий и завершается разработкой модели. В укрупненном плане имитационное моделирование предполагает наличие следующих этапов: