Адаптивные методы среднесрочного прогнозирования модификация метода стохастической аппроксимации

Термин адаптация выступает в 3х аспектах:

Адаптация как св-во системы приспосабливаться к возможным изменениям функционирования; 2) Адаптация как сам процесс приспосабливания адаптивной системы; 3) адаптация как метод, основанный на отработке поступающей информации и приспособленный для достижения некоторого критерия оптимизации.

Под адаптацией понимается способность системы использовать получение новой информации для приближения своего поведения и структуры к оптимальным.

Если системы не адаптируются, то они перестают функционировать оптимально и перестают существовать. Адаптация не происходит мгновенно, а происходит постепенно в силу инерционности большинства систем. В процессе адаптации системы эволюционируют. Это св-во необходимо учесть в прогнозировании. Прогнозные модели должны быть адаптивными:

· Для целей краткосрочного прогнозирования это означает необходимость «уловить» последние по времени сиюминутные отклонения от сложившихся тенденций, которые вызваны кратковременным действием некоторых факторов.

· В случае среднесрочного прогнозирования нет смысла учитывать текущие кратковременные отклонения от сложившихся тенденций – они в скором времени прекратятся. Необходимо «уловить» наметившиеся в последние моменты наблюдений неминуемые изменения в тенденциях развития, и, учитывая их, откорректировать прогнозную модель.

Все методы по использованию принципа адаптации делятся на: 1) Методы корректировки коэффициентов прогнозных моделей и 2) методы взвешивания данных. В первой группе наиболее эффективным считается применение метода стохастической аппроксимации.

Объект управления настолько сложен, что рассматривается как «черный ящик»:

Если перед исследователем стоит задача найти такое упр. воздействие X на систему, чтобы на выходе из нее было достигнуто некое оптимальное значение Y, численно равное наперед заданному U, то для этого используют управляющее воздействие. В допустимой области X берем произвольно x[0], проводим эксперимент с данным значением входа в систему и наблюдаем на выходе некоторое значение Y(x[0]). У исследователя есть первая пара взаимосвязи между входной переменной и выходной. Если бы отклик был стационарным, можно было бы с помощью конечного множества наблюдений собрать достаточное множество пар {x[n], Y(x[n])} и оценить коэффициент регрессии взаимосвязи, с помощью которого можно решить задачу. Но изучаемый объект нестационарен.

Для поиска оптимального значения х выбирают убывающую с ростом n последовательность положительных чисел γ[n]. Необходимо определить такое значение x₁ принадлежащие множеству X₁, чтобы: Y(x)=U. Для выбора значения X в следующем эксперименте используется рекуррентное соотношение Роббинса-Монро:

. - параметр демпфирования колебаний.

Алгоритмы метода стохастической аппроксимации:

· С постоянным шагом . Напр. ½.

· С переменным шагом . Напр. 1/n+1

· С нелинейным шагом . Напр.

Цель адаптации: изменение параметров эк модели, чтоб расчетное значение показателя наилучшим образом приближалось к некот оптим знач . Предмет адаптации: коэф-ты эконометрич мод. Ожидаемые рез-ты адаптации: корректировка коэф-ов мод, чтоб она вернулась в заданные границы изменения обусловленные действием случ факторов.

Алгоритм адаптации: пусть имеется ад модель . Выразим каждый параметр . Если теперь в полученное выражение подставить вместо расчетного значения показателя Y его фактическое значение, то будет получен такой параметр , который в точности описывает фактическое наблюдение на каждом t без какой-либо ошибки аппроксимации: ). Модификация алгоритма Роббинса-Монро будет иметь вид: .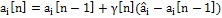

Для линейной модели: .

· Нижняя граница: .

· Верхняя граница: . .

Адаптация модели не происходит в том случае, если

Если , то , и .

и .

.

Для многофакторной модели:

.

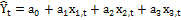
Для нелинейной модели:

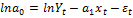
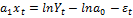
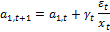
3.Адаптивные методы среднесрочного прогнозирования: методы дисконтирования.

При среднесрочном прогнозировании необходимо адаптировать модель к намечающимся отклонениям от тенденции.

Желание совместить аппарат математической статистики с новым подходом к прогнозированию, открытым Брауном, привёл к тому, что к началу 70-х годов ХХ века появился метод дисконтирования оценок МНК, который позволяет при оценивании параметров моделей учесть текущую информацию в большей степени, чем прошлую и приспособить модель к более поздним данным и использовать при дисконтировании веса, заданные по методу Брауна.

Критерий МНК, как известно, имеет вид: .

В соответствии с ним, находятся такие оценки прогнозной модели, при которых минимизируется сумма квадратов отклонений фактических значений от расчётных. Но для прогнозиста в случае прогноза эволюционно протекающих процессов важнее более точно описать последние наблюдения, нежели те, которые убывают в прошлое. Поэтому и ошибка аппроксимации последних наблюдений должна минимизироваться в большей степени, чем ошибки аппроксимации в начале ряда. Логично, поэтому задать этим ошибкам аппроксимации некоторые веса v_t так, чтобы их значения уменьшались с убыванием наблюдений в прошлое: v_T> v_T-1> …> v_t>…> v₁ и т.д. Веса могут задаваться в числовой форме или в виде функциональной зависимости, но так, чтобы по мере продвижения в прошлое веса убывали. Для удобства часто вводят дополнительное условие: . Но его выполнение, в отличие от ситуации метода Брауна, не является обязательным.

Возможно два варианта дисконтирования оценок МНК.

Первый вариант когда взвешивается каждая ошибка аппроксимации, и эта взвешенная величина подставляется в сумму квадратов МНК. Тогда критерий взвешенного МНК будет иметь вид: .

Применение этого критерия, например, для простой однофакторной линейной модели приведёт к необходимости решать такую систему уравнений:

Такой способ взвешивания данных о наблюдении при построении адаптированных моделей используют не очень часто, поскольку в полученной системе уравнений не ясен смысл взвешивания различных сумм, поскольку веса везде представлены квадратами. Значительно чаще используется другой метод взвешивания, а именно, взвешиваются не сами ошибки аппроксимации, а их квадраты.

Тогда критерий МНК, взвешенного таким способом, имеет вид: .

Использование этого критерия, например, для линейной однофакторной модели приведёт к необходимости решения системы двух таких уравнений: (1).

Левая часть 1го уравнения означает вычисление взвешенной средней переменной , а второе слагаемое этого же уравнения представляет собой произведение коэффициента на взвешенную среднюю переменной .

Веса задаются как и в модели Брауна:

Этот способ задания весов позволяет получить взвешенную среднюю: , которая в краткосрочном прогнозировании используется как лучшая прогнозная оценка данного показателя Y на шаг вперёд.

Этот же способ взвешивания применяется и для факторной переменной : . Поскольку для метода Брауна сумма весов равна единице получим: , где , и . Для успешного применения с помощью весов метода Брауна взвешенного МНК необходимо оптимизировать постоянную сглаживания α.

Суть взвешенного МНК:

Систему уравнений (1) можно получить с помощью общей схемы оценивания методом z-множителей, если задать z-множители так: 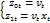. Решая систему (1) мы получаем такие оценки коэффициентов прогнозной модели которые применительно к рассматриваемому случаю будут иметь вид: . Смысл первого уравнения системы очевиден, поскольку веса заданы по методу Брауна и они убывают в прошлое – прогнозная модель будет описывать исходный ряд данных так, что ошибки аппроксимации, убывающие в прошлое, будут больше, чем ошибки аппроксимации последних наблюдений. При этом модель обязательно будет иметь как положительные, так и отрицательные ошибки аппроксимации, иначе сумма взвешенных ошибок аппроксимации не будет равна нулю. Модель, как следует из сказанного, хорошо описывает текущие наблюдения и плохо – прошлые. Смысл второго уравнения системы менее ясен. Будет равна нулю сумма взвешенных произведений фактических значений фактора на ошибки аппроксимации. Но метод z-множителей не только позволяет получить дополнительное толкование оценкам взешенного МНК, но и, используя общий принцип учёта текущих наблюдений в большей степени, чем более ранние, получить новые оценки. Например, можно задать такие z-множители:

. Тогда будет получена такая система уравнений: . Решая эту систему, прогнозист получит оценки адаптировной модели – ведь текущая информация используется в большей степени, чем прошлая, но эти оценки будут отличаться от оценок взвешенного МНК и, возможно, в некоторых случаях будут давать более точные прогнозы. Ряд различных способов дисконтирования данных, который открывает метод z-множителей, довольно широк. Это вооружает прогнозиста новым дополнительным инструментом построения адаптивных моделей среднесрочного прогнозирования.

Недостатком этого способа получения оценок прогнозной модели с помощью взвешенного МНК является показательный способ задания весов ошибок аппроксимации. Зачастую в экономике встречаются ситуации когда после некоторого периода использования новых технологий предприятие возвращается по различным причинам к старым технологиям. Тогда вес наблюдений в прошлом, когда использовались старые технологии, не будут менее важны для прогнозирования, чем текущие.