Пусть индивид может быть занятым (E), безработным (U) или не быть ни тем, ни другим, т.е. не работать и одновременно не удовлетворять хотя бы одному из признаков безработного (не имеет работы в данный момент, активно ищет работу, готов приступить к работе на имеющихся условиях). Назовем таких индивидов «не участвующими» и будем обозначать соответствующее состояние N, а количество «не участвующих» в период t – посредством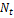 
.
В рассматриваемом регионе имеет место фрикционная безработица, т.е. безработица, связанная с несовершенством механизма рынка труда, а значит, порождающая временные затраты, связанные с поиском работы:
;
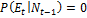Согласно региональному законодательству, каждый индивид обязан проработать, по крайней мере, один период перед тем, как выйти на пенсию:
;
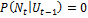Кроме того:
;
;
;
.
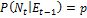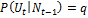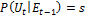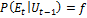Т.о. матрица переходных вероятностей имеет вид:
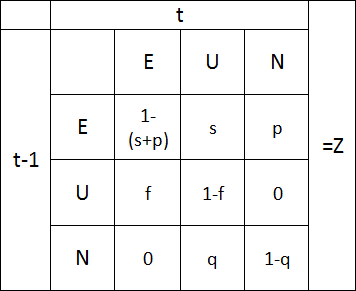Предполагается, что общая численность экономически активного населения региона постоянна и равна 
.
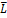Другими словами в момент t выполняется равенство:
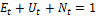. (1)
Математическое ожидание числа занятых в период t:
;
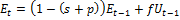Математическое ожидание числа не участвующих в период t:
;
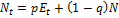Т.к.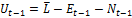 
, то:
.
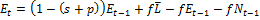Динамическая система представляет собой неоднородную систему двух линейных разностных уравнений:
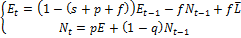; (2)
Найдем стационарное состояние:
;
;
;
;
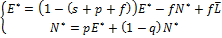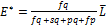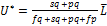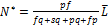Коэффициенты при 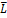представляют собой характеризующие стационарную траекторию рынка труда доли занятых, безработных и «не участвующих» в общей численности населения.
Устойчивость стационарного состояния. В силу условия (1) достаточно исследовать на устойчивость стационарное состояние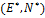 
линейной системы (2). Рассмотрим матрицу коэффициентов этой системы:
;
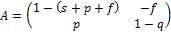Критерий устойчивости – все собственные числа матрицы коэффициентов должны быть меньше 1 по модулю. Собственные числа матрицы определяются из следующего уравнения: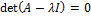 
.
Сначала установим, являются ли собственные значения матрицы А вещественными или комплексно сопряженными. Рассмотрим дискриминант характеристического многочлена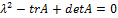 
.
;
;
;
.
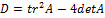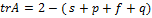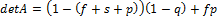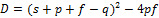1. 
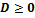. Собственные числа матрицы – вещественные. Характеристический многочлен 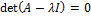представлен в виде 
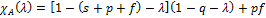(3). Предположим ур-ние (3) 
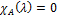имеет вещественный корень 
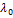, такой, что выполнено неравенство: 
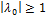, кот равносильно выполнению ровно одного из двух неравенств 
, 
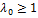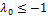. При 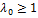имеет место неравенство 
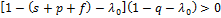, т.к. 
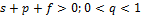. Тем боле справедливо неравенство 
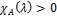, т.к. 
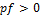. Т.о. 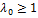не явл корнем характеристического многочлена. Если же 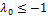, то неравенство 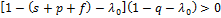также справедливо, т.к. имеет место цепочка соотношений: 
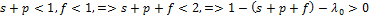. С другой стороны, 
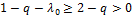. Т.о. снова 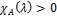, и 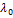не явл корнем характер.многочлена. Итак, показано, что в случае вещественных собственных значений стационарная траектория устойчива.
2. 
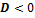. Собственные числа матрицы – мнимые. Если собственные числа матрицы A явл мнимыми, то они образуют комплексно сопряженную пару: 
, 
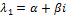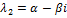. Числа 
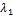и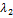 
имеют равные модули: 
, 
.
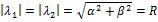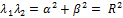С другой стороны, определитель матрицы равен произведению ее собственных значений: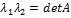 
.
Тем самым,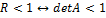 
.
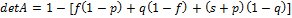. Т.к. в квадратных скобках стоит положит.число, 
,=>, 
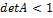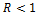. Но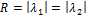 
, значит, оба собственных значения имеют модуль, меньший 1. 
Т.о. устойчивость стационарной траектории доказана, как для вещественных, так и для комплексных корней.
