С источниками напряжений
Идея метода контурных токов основана на доказательстве о том, что вдоль каждого контура протекает независимый ток, называемый контурным.
Токи в ветвях определяются совместным действием контурных токов протекаемых по этим ветвям.
В качестве примера рассмотрим электрическую цепь, приведенную на рисунке 2.17.

Рисунок 2.17 – Электрическая цепь
Граф данной схемы, с выделенными ветвями связи и дерева, приведен на рисунке 2.18. В схеме три независимых контура, вдоль которых протекают контурные токи 

 .
.
В ветвях связи протекает только один контурный ток, соответственно равный 
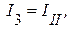
 .
.
В ветвях дерева – несколько токов, соответственно равных:
 ,
, 

Из вышеуказанного следует, что достаточно рассчитать контурные токи, по которым легко определяются токи в ветвях.

Рисунок 2.18 – Граф исходной электрической цепи
Систему уравнений для определения контурных токов можно получить из уравнений Кирхгофа, которые для вышеуказанной схемы (рис. 2.17), имеют вид:
По первому закону Кирхгофа
 ;
;
 ;
;
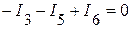 .
.
По второму закону Кирхгофа:
 ;
;
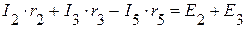 ;
;
 .
.
Из уравнений, составленных по первому закону Кирхгофа, выразим токи в ветвях дерева через токи ветвей связи. Принимая во внимание, что токи в ветвях связи равны контурным токам, имеем:
 ;
;
 ;
;
 .
.
Полученные выражения подставим в уравнения второго закона Кирхгофа. В результате имеем:
 ;
;
 ;
;
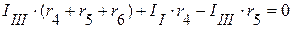 .
.
Таким образом, получили систему трех уравнений с тремя неизвестными токами. Проанализируем свойства полученной системы уравнений. При составлении уравнения для I контура, контурный ток  умножаем на сумму сопротивлений ветвей первого контура
умножаем на сумму сопротивлений ветвей первого контура 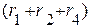 . Влияние второго контурного тока на первый, осуществляется введением выражения
. Влияние второго контурного тока на первый, осуществляется введением выражения  . Здесь
. Здесь  - сопротивление ветви, принадлежащей одновременно и I и II контурам. Знак ”+” перед выражением
- сопротивление ветви, принадлежащей одновременно и I и II контурам. Знак ”+” перед выражением  указывает на то, что контурные токи
указывает на то, что контурные токи 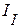 и
и 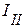 во второй ветви, направлены в одну сторону. Влияние третьего контурного тока на первый, осуществляется введением выражения
во второй ветви, направлены в одну сторону. Влияние третьего контурного тока на первый, осуществляется введением выражения  . Здесь
. Здесь  - сопротивление ветви, принадлежащей одновременно и I и III контурам. Знак ”+” перед выражением
- сопротивление ветви, принадлежащей одновременно и I и III контурам. Знак ”+” перед выражением  указывает на то, что контурные токи
указывает на то, что контурные токи 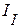 и
и  в четвертой ветви сонаправлены.
в четвертой ветви сонаправлены.
Аналогичными свойствами обладают уравнения, составленные для II и III контура.
Используя вышеуказанные свойства, составим уравнения для определения контурных токов произвольной схемы.
Допустим, имеется цепь, включающая n независимых контуров.
Имеем n независимых токов, и n – уравнений с n – неизвестными. Система уравнений для определения токов имеет вид:
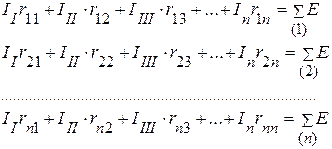 ,
,
где  – соответственно сумма сопротивлений ветвей I, II … n – ного контура;
– соответственно сумма сопротивлений ветвей I, II … n – ного контура;
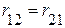 – сумма сопротивлений, принадлежащих I и II контурам - ветви дерева;
– сумма сопротивлений, принадлежащих I и II контурам - ветви дерева;
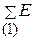 - контурная ЭДС первого контура, равная алгебраической сумме ЭДС ветвей первого контура.
- контурная ЭДС первого контура, равная алгебраической сумме ЭДС ветвей первого контура.
Правило знаков: элементы, содержащие  , всегда принимаются со знаком ”+”. Знаки на разноименных элементах
, всегда принимаются со знаком ”+”. Знаки на разноименных элементах  ,
, 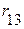 ,
, 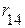 и т.д., определяются совместным направлением контурных токов в указанных ветвях. При совпадении контурных токов ставят знак ”+”, при встречном – знак ”-”. Знаки ЭДС пишутся также как и по второму закону Кирхгофа.
и т.д., определяются совместным направлением контурных токов в указанных ветвях. При совпадении контурных токов ставят знак ”+”, при встречном – знак ”-”. Знаки ЭДС пишутся также как и по второму закону Кирхгофа.
Пример 2.6. Рассмотрим рекомендованный порядок расчета на примере электрической цепи, приведенной на рисунке 2.19, параметры которой E4 = 60 (B), Е5 = 20 В, Е6 = 40 В, r1 = 6 Ом, r2 = 10 Ом, r3 = 9 Ом, r4 = 8 Ом, r5 = 10 Ом, r6 = 7 Ом.

Рисунок 2.19 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы.
1.1. Количество ветвей –  , количество узлов –
, количество узлов –  .
.
1.2. Вычерчиваем граф схемы. Для данной схемы граф имеет вид, представленный на рисунке 2.20.
Ветвями дерева приняты ветви 4,5,6, ветвями связи – ветви 1,2,3.

Рисунок 2.20 – Граф исходной электрической цепи
1.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1 -ю ветвь связи, дополненную 4 и 5 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 2, дополненной 4 и 6 ветвями дерева; третий главный контур состоит из ветви связи 3, дополненной 5 и 6 ветвями дерева. Положительное направление обхода контура рекомендуется принимать совпадающим с направлением тока в ветви связи.
2. Составляем уравнения для определения контурных токов:
 ;
;
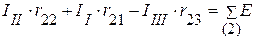 ;
;
 .
.
3. Подставляем числовые значения и решаем систему уравнений:
3.1. Контурные сопротивления
 Ом;
Ом;
 Ом;
Ом;
 Ом.
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
 Ом;
Ом;
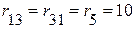 Ом;
Ом;
 Ом.
Ом.
Контурные ЭДС  В;
В;
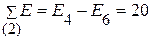 В;
В;
 В.
В.
3.2. После подстановки цифровых данных система имеет вид

3.3. Решая данную систему уравнений, определяем контурные токи:
 А,
А,
 А,
А,
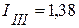 А.
А.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.19.
 А;
А;
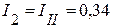 А;
А;
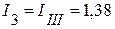 А;
А;
 А;
А;
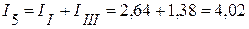 А;
А;
 А.
А.
4. Проверяем решение системы уравнений, составив баланс мощностей.
4.1. Мощность источников:
 Вт,
Вт,
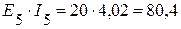 Вт,
Вт,
 Вт.
Вт.
Суммарная мощность источников:
 Вт.
Вт.
4.2.Мощность приемников:
 Вт,
Вт,
 Вт,
Вт,
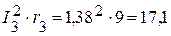 Вт,
Вт,
 Вт,
Вт,
 Вт,
Вт,
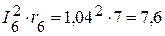 Вт,
Вт,
Суммарная мощность приемников:

 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений  и не превышает 0,5%.
и не превышает 0,5%.
Пример 2.7. Рассмотрим решение задачи, приведенной в примере 2.2, методом контурных токов. Электрическая цепь для рассматриваемого метода, приведена на рисунке 2.21.

Рисунок 2.21 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы.
Количество ветвей –  , количество узлов –
, количество узлов –  .
.
2. Составляем уравнения для определения контурных токов:
 ;
;
 ;
;
 .
.
3. Подставляем числовые значения и решаем систему уравнений:
3.1. Контурные сопротивления
 Ом;
Ом;
 Ом;
Ом;
 Ом.
Ом.
Сумма сопротивлений, принадлежащих нескольким контурам
 Ом;
Ом;
 Ом.
Ом.
Контурные ЭДС  В;
В;
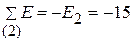 В;
В;
 В.
В.
3.2. После подстановки цифровых данных система имеет вид
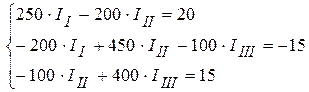
3.3. Решая данную систему уравнений, определяем контурные токи:
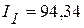 мА,
мА,
 мА,
мА,
 мА.
мА.
3.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.21.
 мА;
мА;
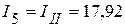 мА;
мА;
 мА;
мА;
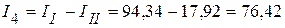 мА;
мА;
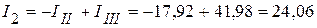 мА.
мА.
Токи в ветвях, рассчитанные в примерах 2.2 и 2.7, совпадают.






